8.3. Чистый изгиб балки

Рассмотрим чистый изгиб балки моментами пар сил М, приложенными в продольной плоскости симметрии балки (рис. 8.5). Под действием этих моментов балка деформируется. Верхние слои балки сжимаются, а нижние растягиваются. Длина волокон, лежащих в плоскости перпендикулярной плоскости самого изгиба в проходящей через продольную ось волокон, при деформации изгиба не изменяются. Совокупность этих волокон образует так называемый нейтральный слой ОО₁.

При этом делается предположения, что поперечные сечения балки плоские до деформации остаются плоскими и нормальными продольной оси балки и при чистом изгибе балку можно рассматривать как совокупность волокон – слоев , подвергающихся деформации простого растяжения или сжатия, а для деформаций справедлив закон Гука и все волокна какого-либо слоя равноудаленного от нейтрального, деформируются одинаково и одновременно.

Это означает, что деформации волокон и возникающие в них нормальные напряжения для данного слоя балки- постоянны. Выделим элемент длиной dx (рис. 8.5) и рассмотрим его деформацию

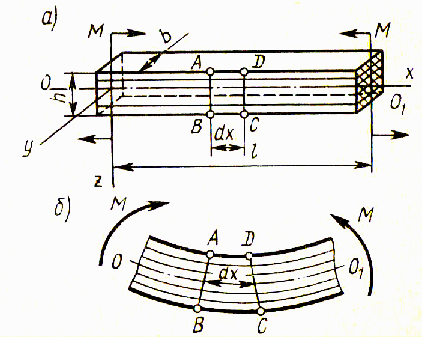
Рис. 8.5. Чистый изгиб балки

Относительное удлинение слоя bc, удаленного от нейтральной оси z равно

, (8.12)

где ; ; - радиус кривизны оси элемента, - элементарный центральный угол, соответствующий дуге dx.

Относительное удлинение тогда равно

. (8.13)

При деформации возникают только нормальные напряжения , значение которых в слое расположенном на расстоянии z от нейтрального слоя по закону Гука равно

, (8.14)

где E – модуль упругости материала при растяжении; распределяются по сечению неравномерно, увеличиваясь пропорционально расстоянию z от нейтрального слоя.

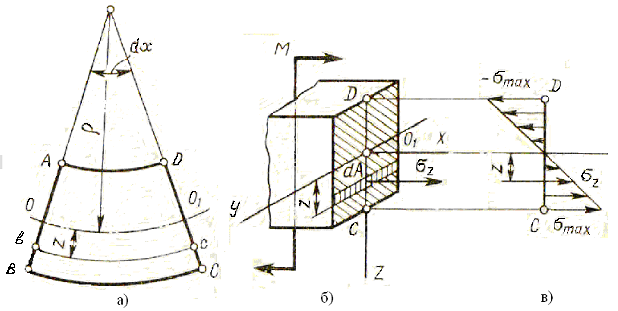
Рис. 8.6. Напряжения и деформации при чистом изгибе

Изгибающий момент M должен быть уравновешен моментом внутренних сил в данном сечении балки. Это условие выражается уравнением равновесия , из которого следует

, (8.15)

подставляя (8.14) получаем

, (8.16)

где учтено, что радиус кривизны не зависит от положения площадки dA и поэтому вынесено за знак интеграла.

Величина называется осевым моментом инерции поперечного сечения балки. С учетом этой величины уравнение принимает вид

. (8.17)

Отсюда находим с учетом (8.17) зависимость напряжения от изгибающего момента в данном сечении

. (8.18)

Таким образом, при чистом изгибе деформация балки протекает в виде растяжения и сжатия ее продольных слоев, удлинение или укорочение слоев происходит тем больше, чем дальше расположены они от нейтрального слоя. В любом поперечном сечении балки возникают нормальные напряжения , значение которых изменяется по высоте пропорционально расстоянию z от нейтрального слоя, а наибольшие напряжения возникают в наиболее удаленных от нейтральной оси, т.е. в поверхностных слоях балки. Значения их равны

, (8.19)

где представляет осевой момент сопротивления поперечного сечения. Если силовые нагрузки действуют на балку в горизонтальной плоскости XY изгиб происходит в этой плоскости и формулы принимают вид

, (8.20)

, (8.21)

Моменты и являются геометрическими характеристиками поперечных сечений балки и характеризуют сопротивление деформации изгиба.

Контрольные вопросы

1. Охарактеризуйте гипотезы, которые используются при кручении вала.

2. Что является мерой интенсивности деформации кручения?

3. Как определяются напряжения при кручении?

4. От чего зависят максимальные напряжения при кручении?

5. Каким будет условие прочности в опасном сечении при деформации кручения?

6. Что называется стрелой прогиба детали?

7. Какие существуют виды опор и их опорные реакции?

8. Охарактеризуйте основные виды изгиба.

9. Как определяются деформации и напряжения при чистом изгибе?

10. Где возникают наибольшие напряжения при чистом изгибе балки и как они рассчитываются?

11. От чего зависят нормальные напряжения в слое, расположенном на расстоянии z от нейтрального слоя, при чистом изгибе?