
- •А.И. Андреев и.В. Андреев
- •Воронеж 2015
- •1. Структура механизмов
- •2. Основные виды механизмов
- •3. Кинематический расчет механизмов
- •3.1. Аналитические методы исследования кинематики механизмов
- •4. Динамика механизмов
- •4.1. Силы, действующие на звенья
- •4.2. Определение крутящего момента на ведомом валу
- •4.3. Приведение масс в механизмах
- •4.4. Приведение сил и моментов сил в механизмах
- •5. Уравнения движения механизма
- •5.1. Уравнение движения механизма в интегральной форме, три стадии движения механизма
- •5.2. Механические характеристики электродвигателей
- •5.3. Уравнение движения механизма в дифференциальной
- •5.4. Трение в кинематических парах
- •5.5. Коэффициент полезного действия механизмов
- •6. Деформации и напряжения деталей
- •6.1. Деформация деталей, виды деформаций
- •6.2. Напряжения и метод сечений
- •7. Осевое растяжение и сжатие. Сдвиг
- •7.1. Напряжения и деформации при растяжении
- •7.2. Закон Гука и параметры кривой растяжения образца
- •7.3. Закон Гука для двухосного напряженного состояния
- •7.4. Определение твердости
- •Расчеты на прочность и жесткость
- •Деформации и напряжения при сдвиге
- •7.7. Закон Гука при сдвиге
- •8. Кручение и изгиб
- •8.1 Деформации и напряжения при кручении
- •8.2. Изгиб. Виды изгиба и их особенности. Типы опор и опорные реакции
- •8.3. Чистый изгиб балки
- •9. Характеристики плоских сечений и поперечный изгиб
- •9.1. Геометрические характеристики плоских сечений
- •Плоский поперечный изгиб. Изгибающий
- •Правила построения эпюр изгибающих моментов
- •Напряжения при поперечном изгибе. Расчеты
- •9.5. Прогиб балок. Расчеты на прочность
- •10. Прочность при сложных деформациях
- •10.1. Сложные деформации. Теории прочности
- •10.2. Пространственный изгиб
- •10.3. Совместное действие изгиба и растяжения (сжатия)
- •10.4. Совместное действие изгиба и кручения
- •11. Продольный изгиб. Прочность при переменных напряжениях
- •11.1. Устойчивость сжатых стержней. Формула Эйлера
- •11.2. Проверка сжатых стержней на устойчивость
- •11.3. Переменные напряжения. Выбор допускаемых напряжений
- •Концентрация напряжений и ее влияние
- •11.5. Определение допускаемых напряжений
- •12.4. Геометрические характеристики механизма
- •13. Силовой расчет механизмов
- •14. Расчет механизмов на прочность
- •14.1. Прочностные расчеты фрикционных передач
- •14.2. Износостойкость механизма винт–гайка
- •14.3. Расчет на прочность цилиндрических зубчатых передач
- •14.4. Расчет на прочность червячных передач
- •15. Определение прочности валов и осей механизмов
- •16. Основы конструирования механизмов и отдельных деталей передач
- •Проектирование червяков и червячных колёс
- •Конструирование деталей фрикционных передач
- •Конструкции валов и осей
- •Точность изготовления деталей
- •Размеры. Квалитеты. Система отверстия
- •Точность геометрической формы деталей
- •Заключение
- •Библиографический список
- •Оглавление
- •11. Продольный изгиб. Прочность при переменных
- •394026 Воронеж, Московский просп., 14
8.2. Изгиб. Виды изгиба и их особенности. Типы опор и опорные реакции
Деформацией изгиба принято называть
всякое искривление продольной оси
детали, возникающее в результате действия
силовых нагрузок. На рис. 8.2 изображен
валик с насаженным на него диском. Под
действием силы F валик
прогибается на величину
![]() ,
которая называется стрелой прогиба.
,
которая называется стрелой прогиба.
При деформации изгиба возникают дополнительные внутренние силы взаимодействия частиц материала, оказывающие сопротивление деформации. В случае нарушения условия прочности на изгиб может произойти поломка валика.
Наиболее распространен поперечный изгиб, при котором силы, вызывающие деформацию детали перпендикулярны ее оси. Деталь, подвергающаяся деформации изгиба называют балкой, опорами балки являются подшипники. Принято различать три вида опор: шарнирно- подвижная, шарнирно-неподвижная и жестко защемленная.

Рис. 8.2. Деформация изгиба и стрела прогиба
Шарнирно-подвижная опора допускает некоторый поворот продольной оси балки относительно опоры и поступательное перемещение вдоль опорной поверхности. Нагрузка этой опорой может восприниматься по нормали к опорной поверхности, такую линию действия имеет опорная реакция. Для валика опора такого типа может быть осуществлена посредством подшипника качения, свободно посаженного в корпусе. На рис. 8.3 а показано схематическое изображение этой опоры. Шарнирно – неподвижная опора (рис. 8.3 б) допускает только поворот балки.
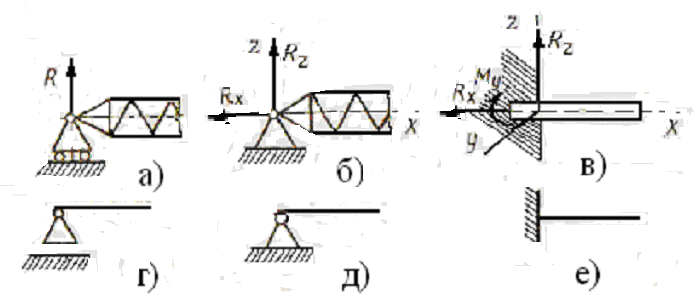
Рис. 8.3. Виды опор (а, б, в) и их условные обозначения (г, д, е)
Если в качестве опоры использовать
подшипник качения, то его наружное
кольцо должно быть закреплено в продольном
направлении. Реакция этой опоры слагается
из двух составляющих
![]() и
и
![]() .
Опора с жестким защемлением конца балки
(рис. 8.3 в) исключает возможность любого
относительного перемещения балки. Такие
балки называют консолями. Реакции жестко
защемленной опоры: составляющие
,
и реактивный момент
.
Опора с жестким защемлением конца балки
(рис. 8.3 в) исключает возможность любого
относительного перемещения балки. Такие
балки называют консолями. Реакции жестко
защемленной опоры: составляющие
,
и реактивный момент
![]() .
При конструировании балок общее число
опорных реакций не превышает возможного
числа уравнений, которые для плоской
системы имеют вид равновесия
.
При конструировании балок общее число
опорных реакций не превышает возможного
числа уравнений, которые для плоской
системы имеют вид равновесия
![]() ,
,
![]() ,
,
![]() .
(8.11)
.
(8.11)
В этом случае число опорных реакций не должно превышать трех. Этому условию удовлетворяют балки с одной шарнирно-неподвижной и одной шарнирно- подвижной опорой, а также консоли. Внешние нагрузки, вызывающие изгиб, удобно разделить на три группы (рис. 8.4).
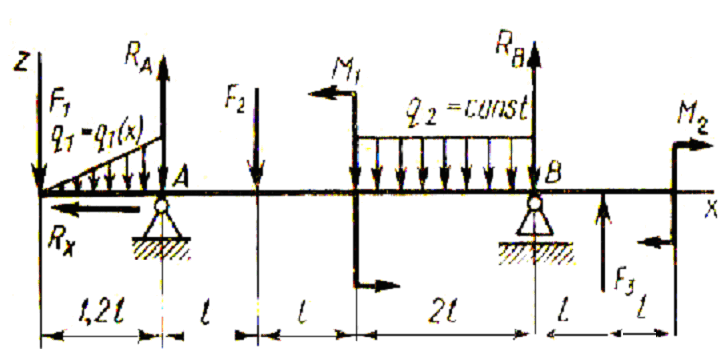
Рис. 8.4. Виды нагрузок и изгибаюших моментов,
действующих на балку
Сосредоточенные силы
![]() ,
сосредоточенные моменты пар сил
,
сосредоточенные моменты пар сил
![]() ,
распределенные по длине балки нагрузки
интенсивностью q.
Равномерная
распределенная
нагрузка имеет вид
,
распределенные по длине балки нагрузки
интенсивностью q.
Равномерная
распределенная
нагрузка имеет вид
![]() и неравномерная
и неравномерная
![]() .
Эти силовые нагрузки могут действовать
как в одной плоскости, так и в разных
продольных плоскостях балки. Если
внешние нагрузки располагаются в одной
плоскости, то такой изгиб принято
называть плоским.
.
Эти силовые нагрузки могут действовать
как в одной плоскости, так и в разных
продольных плоскостях балки. Если
внешние нагрузки располагаются в одной
плоскости, то такой изгиб принято
называть плоским.
При плоском изгибе продольной оси балки всегда протекает в плоскости действия силовых нагрузок.
Балка может также подвергаться изгибу, когда плоскость действия силовых нагрузок не совпадает с плоскостью деформации продольной оси. Такой изгиб называется косым.
Если силовые нагрузки действуют на балку в разных плоскостях – это будет пространственный изгиб.
Если нагрузки таковы, что в любом сечении балки действует только постоянный изгибающий момент, а поперечные силы равны нулю, то изгиб называют чистым.
