6. Деформации и напряжения при сдвиге

Некоторые детали механических систем (заклепки, штифты) подвергаются такой нагрузке, при которой их деформация протекает в виде относительного смещения поперечного сечений. Пусть на деталь 1 (рис. 7.3) нормально к ее продольной оси действуют близко расположенные силы F и , которые равны по величине и противоположны по направлению. Выделенный в зоне деформаций элемент (рис. 7.3 а) показывает смещение его граней, которое называется чистым сдвигом. Количественными характеристиками деформации сдвига являются абсолютный или линейный сдвиг z и относительный сдвиг z /x, являющийся мерой перекоса углов элемента. При деформации элемента в пределах упругости значение z /x мало и его можно выразить через угол сдвига

. (7.16)

При чистом сдвиге на гранях элемента возникают касательные напряжения  (рис. 7.3 б). Эти напряжения  распределяются по площади сечения A равномерно, и их значение может быть найдено из условия, что равнодействующая внутренних сил уравновешивает внешнюю нагрузку F.

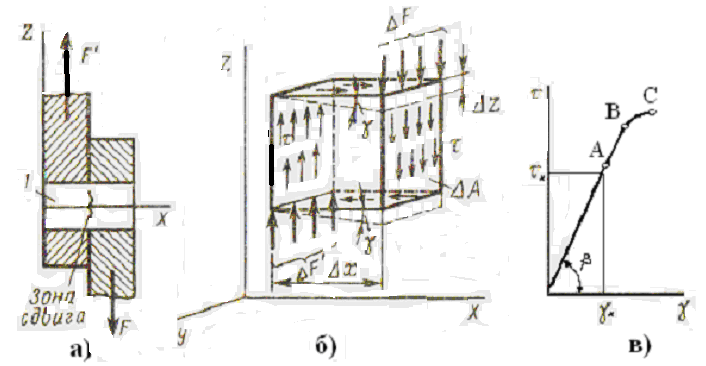
Рис. 7.3. Деформации и напряжения сдвига

Тогда для поперечного сечения детали следует

, (7.17)

откуда

, (7.18)

где F нагрузка, вызывающая деформацию сдвига, A – площадь сечения. При достижении касательными напряжениями некоторого опасного значения _оп в материале детали возникает, либо состояние текучести для пластичных материалов, либо разрушение (срез) для хрупких материалов. Условие прочности на сдвиг принимает вид

, (7.19)

где [] – допускаемое напряжение ([]=_оп/n) для пластичных материалов можно принимать []=0,5-0,6 [_P] и []=0,8-1,0 [_P] для хрупких, [_P]-допускаемое напряжение при растяжении.

7.7. Закон Гука при сдвиге

При деформации деталей на сдвиг в пределах упругости установлено, что касательные напряжения  пропорциональны значению относительного сдвига .

Точка В (рис 7.3 в) соответствует пределу упругости _у материала образца. Для любой точки А прямой ОВ, _к /_к=G, откуда

 = G , (7.20)

где G- коэффициент пропорциональности, который называется модулем сдвига. Зависимость (7.20) выражает закон Гука при сдвиге Установлено,. что между модулем упругости при растяжении E и при сдвиге G существует связь

. (7.21)

Если принять коэффициент Пуассона для стали =0.3, то G=

0.4E.

Контрольные вопросы

1. Что называют осевым растяжением и сжатием детали?

2. Как связана относительная поперечная деформация с продольной деформацией?

3. Охарактеризуйте закон Гука и параметры кривой растяжения образца.

4. Запишите закон Гука для двухосного напряженного состояния детали.

5. Как определяется твердость детали по Бринеллю и Роквеллу?

6. Каким будет условие прочности детали при осевом растяжении?

7. Что понимают под допускаемом напряжении при осевом растяжении детали?

8. Как определяются деформации при сдвиге?

9. Какие напряжения возникают при сдвиге и как они определяются?

10. Запишите условие прочности при сдвиге.

11. Как выбирается допускаемое напряжение при сдвиге?

12. Запишите закон Гука при сдвиге.