Задачи и упражнения

1. Доказать, что в неорграфе число вершин с нечетной степенью четно.

2. Построить граф (если он существует) с последовательностью степеней

а) (4,3,3,2,2);

б) (5,4,2,2,1) .

3. Привести примеры сильно связного, связного, несвязного графов.

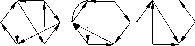4. Среди графов, изображенных на рис.4.57, указать сильно связный, односторонне связный и несвязный графы.

Рис. 4.57

5. Найти матрицы достижимости и контрдостижимости для графов G₁ ,G₂, G₄, изображенных на рис. 4.57.

6. Доказать, что если в n-вершинном графе степень каждой вершины не меньше, чем (n-1)/2 , то он связен.

7. Доказать, что если G  несвязный граф, то G  связный.

8. Доказать, что в любом графе каждая его база содержит все вершины, имеющие нулевые полустепени захода.

9. Для графов, изображенных на рис. 4.58, найти сильнее компоненты, построить конденсацию, найти базы и антибазы.

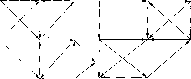
Рис. 4.58

10. Доказать, что хроматическое число каждого n-вершинного дерева (n2) равно 2.

11. Что можно сказать о хроматическом числе объединения двух графов?

12. Граф называется критическим, если удаление любой из его вершин вместе с инцидентными ей ребрами приводит к графу с меньшим хроматическим числом. Показать, что К_n является критическим для любого n>1.

13. Показать, что всякий k-xpoмагический граф (k>l) содержит в качестве подграфа критический k-хроматический граф, и найдите такой подграф для графа на рис. 4.59.

Р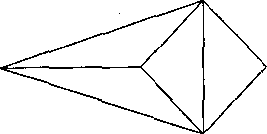 ис.4.59

14. Определить раскраску графов, изображенных на рис. 4.60.

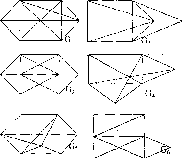
Рис. 4.60

15. Построить остовы для графов, изображенных на рис. 4.61.

Рис. 4.61

16. Доказать, что граф G является связным тогда и только тогда, когда он имеет остов.

17. Существует ли эйлеров цикл в графах, изображенных на рис. 4.62 ?

Рис. 4.62

18. Определить, какие из графов пяти правильных многогранников имеют эйлеровы циклы.

19. Составить алгоритм, основанный на алгоритме Флери и позволяющий найти все эйлеровы циклы графа.

20. Определить гамильтоновы пути и контуры методом перебора Робертса и Флореса в графах, изображенных на рис. 4.63.

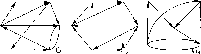
Рис. 4.63

21. Для графа построить, если это возможно, его уклад­ку на плоскости.

а) б)

в) г)

д )

е)

5. Комбинаторика

Комбинаторика – раздел математики о выборе и расположении элементов некоторого множества на основании каких-либо условий.

Комбинаторика стала выделяться в отдельный раздел математики в работах Б. Паскаля и Л. Ферма, хотя отдельные понятия и факты комбинаторики были известны ещё математикам античности и средневековья. Большой вклад в развитие комбинаторики внесли Г. Лейбниц, Я. Бернулли, Л. Эйлер. В их работах были даны определения основных понятий комбинаторики, развиты первые комбинаторные методы и указаны их применения, а также прослежена связь комбинаторики с исчислением вероятностей. Именно комбинаторика послужила фундаментальной основой началам теории вероятностей. При решении комбинаторных задач часто применяются два важных правила: умножения и сложения.

Правило умножения. Пусть требуется выполнить одно за другим какие-то k действий. Если первое действие можно выполнить n₁ способами, второе действие - n₂ способами, третье - n₃ и так до k – го действия, которое можно выполнить n_k способами, то все k действий вместе могут быть выполнены n₁n₂ n₃ n_k способами.

Правило сложения. Если два действия взаимно исключают друг друга, причем одно из них можно выполнить m способами, а другое – n способами, то выполнить одно любое из этих действий можно n + m способами.