2.6. Обратное z-преобразование

По определению, есть обратное z-преобразова­ние от . Оно может быть найдено из (2.7) с помо­щью интегральной теоремы Коши. Сначала умножим обе части (2.7) на , а затем произведем интегрирование по замкнутому контуру обеих частей равенства. Если контур интегрирования лежит внутри областей сходимо­сти бесконечного ряда (2.7), то операции суммирования и интегрирования можно поменять местами, что даст

(2.8)

Теорема Коши гласит, что если контур интегрирова­ния охватывает начало координат, то для всех k, за исключением . Для интеграл стано­вятся равным . Применяя это к выражению (2.8). получаем теорему об обратном z-преобразовании:

(2.9)

Пусть . Тогда . Для подтверждений того факта, что есть обратное z-преобразование от , применим (2.9), выполняя ин­тегрирование вдоль окружности радиуса, большего, чем К. Это дает:

(2.10)

Уравнение (2.10) решается с помощью теоремы о вычетах, дающей , если контур интегрирования охватывает полюс при . Таким образом, подходя­щим контуром является окружность радиусом , показанная на рис. 2.7, где может быть взято как угод­но малым. Однако в этом случае может быть также использован контур или любой другой контур, охваты­вающий полюс.

Если , то согласно изложенному в § 2.5 область сходимости лежит вне единичной окружности на комплексной z-плоскости. В большинстве случаев, последовательность не представляет физического ин­тереса при , поскольку такая последовательность бесконечно растет с ростом n и может быть классифицирована как неустойчивая.

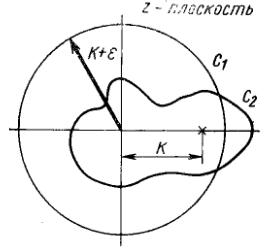
Рис. 2.7 Возможные контуры интегрирования для обратного z-преобразования

Таким образом, единичная окружность будет наименьшей окружностью на z-плоскости из тех, что находится внутри области сходимости для всех устойчивых последовательностей вида . Эго свой­ство единичной окружности может быть распространено на все другие устойчивые последовательности, и этим объясняется широкое применение единичной окружности как контура интегрирования для обратного z-преобразования.

2.7. Теорема о свертке

Пусть есть z-преобразование от , а есть z-преобразование oт . Тогда покажем, что если есть z-преобразование от , то

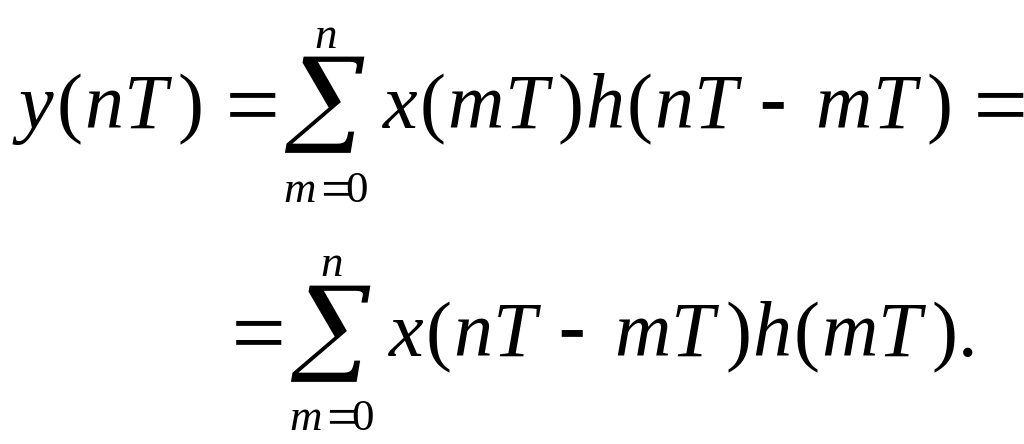(2.11)

Простой путь доказательства этого соотношения за­ключается в применении метода индукции при исследо­вании произведения

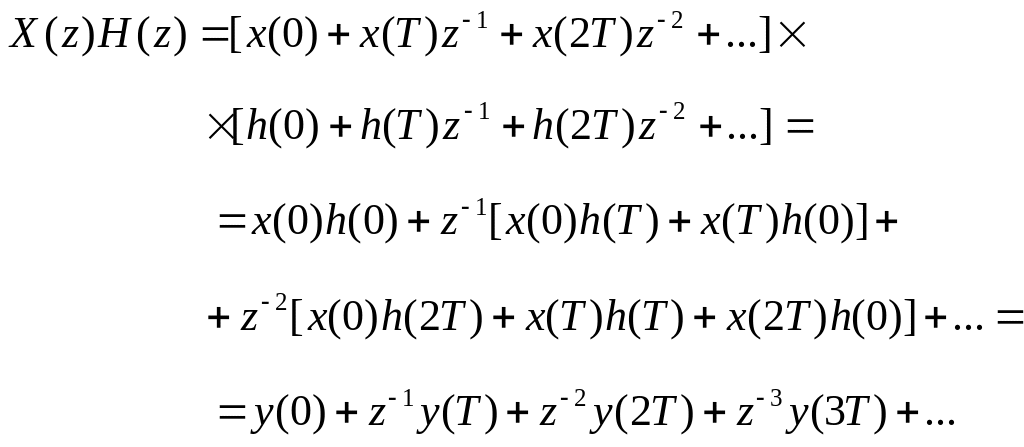(2.12)

Читатель может доказать, что (2.11) справедливо, приравняв в (2.12) коэффициенты при степенях .

Теорема о свертке, как и в аналоговом случае, может быть принята как определяющее уравнение для линейных дискретных систем. Рис. 2.8 иллюстрирует вычисление по формуле (2.11). Пунктирная кривая представляет , а непрерывная кривая представляет .

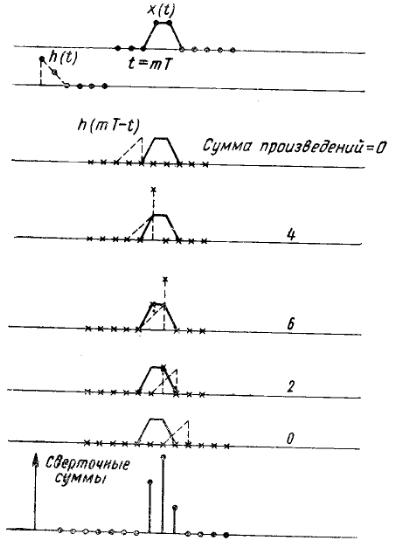
Рис. 2.8 Иллюстрация свертки [xxx обозначают точки на кривой ]

Сумма всех почленных произведений двух последовательностей от до есть сверточная сумма, определяемая выражением (2.11).

Если представляет собой отклик линейной дискретной цепи на единичный импульс (первая строка в табл. 2.1), то (2.11) определяет отклик этой цепи на произвольный входной сигнал .