2.3. Частотная характеристика цепи первого порядка

Наиболее ценным является описание нашей простой системы с помощью ее отклика на синусоидальный вход­ной сигнал. Если на рис. 2.1 принять равным , тогда . Отклик на реальный синусоидальный сигнал, скажем , может быть всегда найден сложением откликов на входные сигналы и . Решение (2.1) для входного сигнала может быть найдено с помощью простой индук­ции. Здесь ми даем только установившееся решение с начальным условием . Оно имеет вид

(2.4)

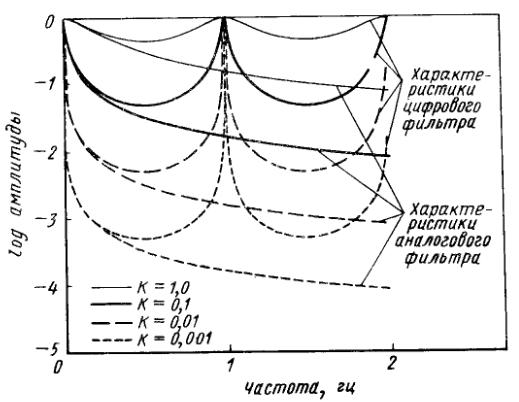
Рис. 2.5 Сравнение частотных характеристик цифрового и аналогового фильтров первого порядка

Как и следовало ожидать, выходной сигнал является комплексно экспоненциальным, подобно входному сигналу, но он изменён в соответствии с передаточной функцией, которую мы определим как

(2.5)

где

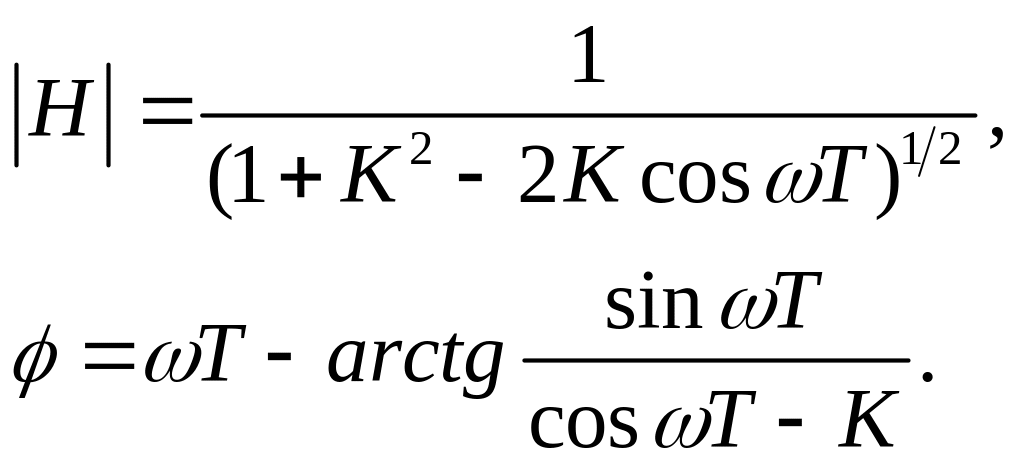(2.6)

Равенства (2.6) выражают частотную избиратель­ность цепи. На рис. 2.5 изображена величина H из (2.6) для различных К и при T=1, из которого мы можем определять сходство и различие между цифровой систе­мой и соответствующей аналоговой системой, такой, как RC-цепь с .

2.4. Геометрическая интерпретация частотной характеристики

Уравнения (2.5) и (2.6) могут быть интерпретированы геометрически с помощью единичной окружности, по­казанной на рис. 2.6.

Из (2.5) видно, что есть , а , так что вектор, соединяющий некоторую точку на окружности (при угле ) и критическую точку на действительной оси, полностью определяет передаточную функцию. В дальнейшем мы увидим также, что эта геометрическая картина может быть обоб­щена для описания линейных цифровых цепей с произвольным числом операций.

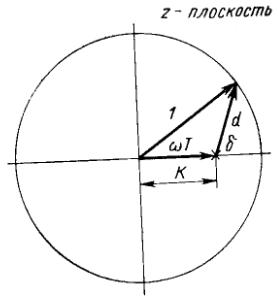
Рис. 2.6 Представление цепи первого порядка в z-плоскости

2.5 Z-преобразование

Ранее было показано, что разностное уравнение пер­вого порядка может быть наглядно представлено передаточной функцией, которая характеризует поведение си­стемы в зависимости от частоты при синусоидально» воздействии. Оказалось так­же возможным изобразить эту передаточную функцию геометрически. Формальным обоснованием для распро­странения такой интерпретации на обобщенное линейное разностное уравнение является z-преобразование, которое допускает над разностными уравнениями такие же алгебраические действия, какие допускает преобразова­ние Лапласа над дифференциальными уравнениями. Исследуем кратко свойства z-преобразования, после этого обсудим линейные разностные уравнения с точки зрения цепей и затем применим методы z-преобразо­вания для нахождения обобщенных решений этих уравнений.

Рассмотрим последовательность чисел , которая образована при дискретизации непрерывного колебания .

Z-преобразование этой последовательности определя­ется как

(2.7)

где z - комплексная переменная, а - функция этой комплексной переменной. Поскольку (2.7) - степенной ряд переменной , то обычно возникает вопрос о схо­димости такого ряда. Гуревич детально исследовал эту проблему, и ниже будет приведено несколько основ­ных результатов из его работы.

Ряд (2.7) сходится для и расходится для , где радиус сходимости R есть верхний предел последовательности .Так, напри­мер, если , то ряд (2.7) сходится вне окруж­ности радиуса K.

Для есть аналитическая функция z. Таким образом, функция, определенная выражением (2.7) и распространенная на всю z-плоскость с помощью аналитического продолжения, может быть названа z-преобразование последовательности . Отсюда следует, что определяется на всей z-плоскости, а выражение (2.7) справедливо только в области сходимости.

В таблице приведены z-преобразования для некоторых наиболее часто встречающихся последовательностей.

Таблица

Название последова-тельности	Последовательность	Z-преобразование последова-тельности
Единичный импульс
Единичный скачок
Комплексная экспонента