
- •Оглавление
- •1. Общие вопросы цифровой обработки сигналгов
- •1.1. Основные расчетные алгоритмы для цифровых фильтров
- •2. Дискретные линейные системы
- •2.1. Модель дискретной линейной системы
- •2.2. Линейное разностное уравнение первого порядка
- •2.3. Частотная характеристика цепи первого порядка
- •2.4. Геометрическая интерпретация частотной характеристики
- •2.6. Обратное z-преобразование
- •2.7. Теорема о свертке
- •2.8. Теорема о комплексной свертке
- •2.9. Решение разностных уравнений первого порядка с помощью z-преобразования
- •2.10. Решение разностных уравнений второго порядка с помощью z-преобразования
- •2.11. Двустороннее z-преобразование
- •2.12. Цепи для разностного уравнения второго порядка
- •3. Расчет цифровых фильтров в частотной области
- •3.1. Синтез цифровых фильтров
- •3.2. Различные методы расчета цифровых фильтров
- •3.3. Применение принципа инвариантности импульсной характеристики
- •3.4. Коэффициент передачи цифровых резонаторов
- •3.5. Расчет цифровых фильтров на основе непрерывных фильтров с нулями на бесконечности
- •3.6. Определение цифрового фильтра с помощью квадрата модуля передаточной функции
- •3.7. Расчет цифровых фильтров путем билинейного преобразования функции непрерывного фильтра
- •3.8. Фильтры на основе частотной выборки
- •3.9 Метод частотной выборки
- •4. Эффекты квантования в цифровых фильтрах
- •4.1. Постановка задачи
- •4.2. Ошибки, вызываемые неточными значениями постоянных параметров
- •4.3. Ошибки, вызываемые аналого-цифровым преобразованием
- •4.4. Ошибки, вызываемые квантованием произведений
- •4.5. Эффект мертвой зоны
- •4.6. Формулы для шума округления при различных реализациях цифровых цепей
- •4.7. Пример. Различные структуры цепи с двумя полюсами и одним нулем
- •5. Дискретные преобразования фурье
- •5.1. Дискретное преобразование Фурье
- •5.2. Алгоритм Герцеля
- •5.3. Быстрое преобразование Фурье
- •Прореживание по времени
- •Прореживание по частоте
- •5.4. Соотношение между прореживанием по времени и прореживанием по частоте
- •Заключение
- •394026 Воронеж, Московский просп., 14
5.2. Алгоритм Герцеля
Существует много методов
вычисления ДПФ для отдельной частоты
.
Самым простым из всех
является непосредственное применение
(5.2). Это требует проведения N
комплексных умножений и N
комплексных сложений
с использованием N
коэффициентов
![]() .
Обычно эти
коэффициенты могут быть восстановлены
из запомненной таблицы отсчетов одной
четверти периода синусоидального
колебания. Комплексное умножение
требует проведения четырех
действительных умножений и двух
действительных сложений, а комплексное
сложение— двух действительных
сложений, так что общий объем вычислений,
заключенный в выражении (5.2), составляет
.
Обычно эти
коэффициенты могут быть восстановлены
из запомненной таблицы отсчетов одной
четверти периода синусоидального
колебания. Комплексное умножение
требует проведения четырех
действительных умножений и двух
действительных сложений, а комплексное
сложение— двух действительных
сложений, так что общий объем вычислений,
заключенный в выражении (5.2), составляет
![]() ,
(5.35)
,
(5.35)
где
![]() —время,
требуемое для действительного умножения;
—время,
требуемое для действительного умножения;
![]() — время, требуемое
для действительного сложения;
— время, требуемое
для действительного сложения;![]() —
время, требуемое для других операций
при обработке, и М —
число различных вычисляемых частотных
коэффициентов.
—
время, требуемое для других операций
при обработке, и М —
число различных вычисляемых частотных
коэффициентов.
Другим алгоритмом для
вычисления коэффициента на отдельной
частоте является алгоритм Герцеля,
основанный на подходе с позиций
цифровой фильтрации. Рассмотрим сначала
фильтр с единственным комплексным
полюсом при
![]() :
:
![]() (5.36)
(5.36)
Здесь впервые вводится фильтр с комплексными коэффициентами, но с ним не связаны какие-либо принципиальные трудности, особенно в том случае, когда фильтруются комплексные данные. Подадим на вход фильтра последовательность х(пТ), для которой желательно вычислить X(kΩ). Так как z-преобразование от х(пТ) есть Х(z), то выходной сигнал фильтра будет равен
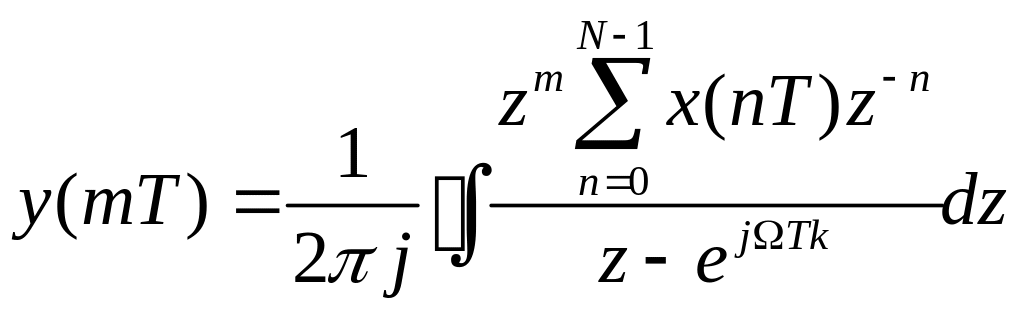 (5.37)
(5.37)
И, в частности, когда
![]() ,
выходной сигнал определяется как вычет
в полосе
,
выходной сигнал определяется как вычет
в полосе
![]() :
:
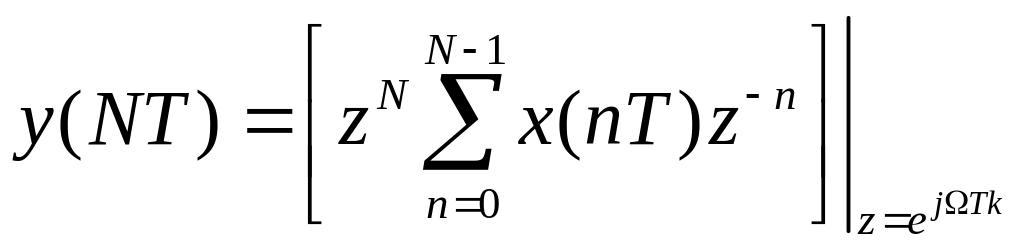 (5.38)
(5.38)
Но поскольку
![]() ,
,
То можно видеть, что
![]() .
(5.39)
.
(5.39)
Применение такого фильтра для вычисления преобразований Фурье не дает экономии в вычислительных операциях, хотя оно уменьшает требуемую память для коэффициентов. Однако, если переписать (5.36) как
![]() ,
(5.40)
,
(5.40)
можно прийти к реализации
цифрового фильтра, показанной на
рис. 5.5. Поскольку значение выходного
сигнала фильтра необходимо иметь только
при
![]() ,
то нет нужды выполнять
действия той части цепи, что находится
справа от пунктирной линии при любом
п, за
исключением случая п
= N.
Таким образом,
требуемые операции состоят из N
умножений действительных коэффициентов
на комплексные данные и 2N
комплексных сложении.
По сравнению с ними объемом заключительных
операций можно пренебречь, если число
отсчетов велико.
,
то нет нужды выполнять
действия той части цепи, что находится
справа от пунктирной линии при любом
п, за
исключением случая п
= N.
Таким образом,
требуемые операции состоят из N
умножений действительных коэффициентов
на комплексные данные и 2N
комплексных сложении.
По сравнению с ними объемом заключительных
операций можно пренебречь, если число
отсчетов велико.
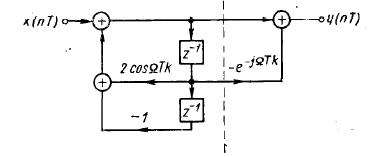
Рис. 5.5. Цифровой фильтр для вычисления одной точки ДПФ с помощью алгоритма Герцеля.
Если пересчитать все к операциям над действительными числами, то получим
![]() (5.41)
(5.41)
где
![]() есть время, требуемое
для особых операций в алгоритме
Герцеля. Если, однако, частоты, при
которых вычисляются Х(kΩ),
могут быть сгруппированы
парами как k
и N-k,
то можно получить
дополнительную экономию, поскольку
только нуль фильтра на рис. 5.5 различен
для этих двух частот. Поэтому, если
частоты могут быть таким путем
сгруппированы в пары, то
есть время, требуемое
для особых операций в алгоритме
Герцеля. Если, однако, частоты, при
которых вычисляются Х(kΩ),
могут быть сгруппированы
парами как k
и N-k,
то можно получить
дополнительную экономию, поскольку
только нуль фильтра на рис. 5.5 различен
для этих двух частот. Поэтому, если
частоты могут быть таким путем
сгруппированы в пары, то
![]() (5.42)
(5.42)
Откуда видно, что алгоритм Герцеля дает экономию примерно в 4 раза по сравнению с прямым способом вычисления по (5.2). Для действительных чисел как прямой метод, так и метод Герцеля дают дополнительную экономию.
