5. Дискретные преобразования фурье

5.1. Дискретное преобразование Фурье

По многим причинам желательно вычислять преобра­зование Фурье на цифровых машинах. Это означает, что необходимо рассматривать только дискретные отсчеты как временной функции, так и спектра и только конечное число отсчетов каждой из них. Предположим, что временная функция f(t) представлена последовательностью из N отсчетов f(nT), где T - интервал дискретизации во временной области.

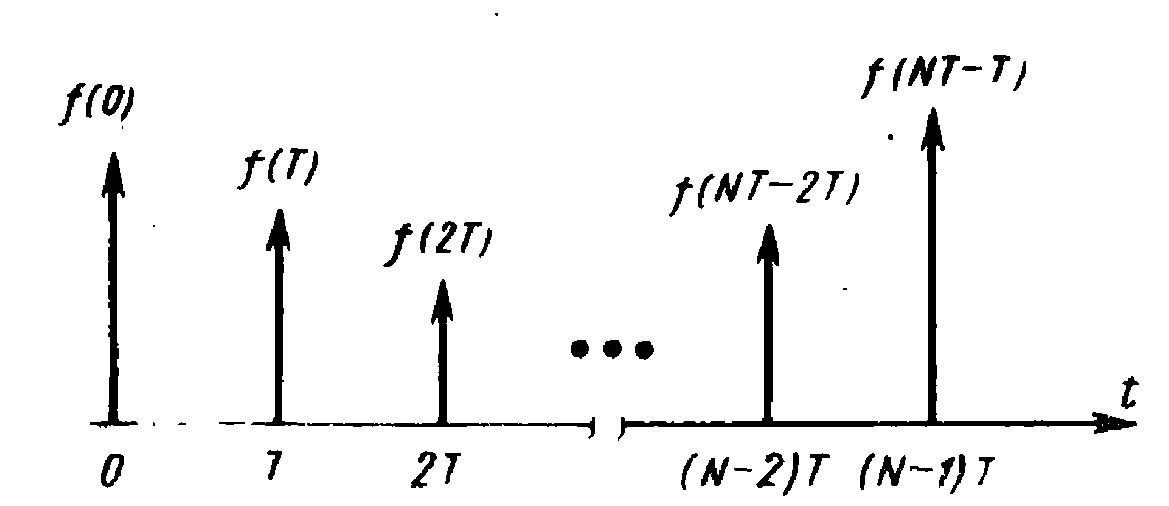
Рис. 5.1. Функция времени, которая может ассоциироваться с после­довательностью отсчетов.

Затем допустим так­же, что спектр F(ω) представлен как F(kΩ), 0≤k≤N-1, гдe Ω - выбранное расстояние между отсчетами в ча­стотной области. Если из последовательности f(nT) сфор­мирована функция f*(t) с конечным числом импульсов, как показано на рис. 5.1, то можно написать выражение для F*(kΩ):

(5.1)

которое полностью дискретно как по времени, так и по частоте и поэтому подходит для вычислений.

Учитывая приведенную выше мотивировку, опреде­ляем дискретное преобразование Фурье (сокращенно ДПФ) от последовательности f(nT) из N отсчетов, как другую последовательность (eсли это не оговорено особо, то подразумевается, что как f(nT) , так и являются комплексными функциями).

(5.2)

^где

(5.3)

При таком определении существует только N различ­ных значений, которые возможно вычислить по (5.2), а именно при . Для того чтобы это доказать, рассмотрим (5.2) для произвольного целого числа k, выраженного как

где по модулю N, а .

Тогда

(5.4)

но поскольку , то последнее выражение можно упростить до вида:

(5.5)

Мы можем считать (5.2) формулой, дающей последо­вательность только из N чисел, или формулой, дающей периодическую последовательность чисел с периодом N. Другими словами, дискретное преобразование Фурье может пониматься как оценка z-преобразования конечной последовательности f(пТ) в N точках на z-плоскости, рав­номерно расположенных вдоль единичной окружности под углами радиан. В некоторых случаях рассмотре­ние последовательности спектральных отсчетов, располо­женных вдоль окружности, подобно тому, как это изображено на рис. 5.2, вместо отсчетов, расположенных вдоль линии, очень полезно.

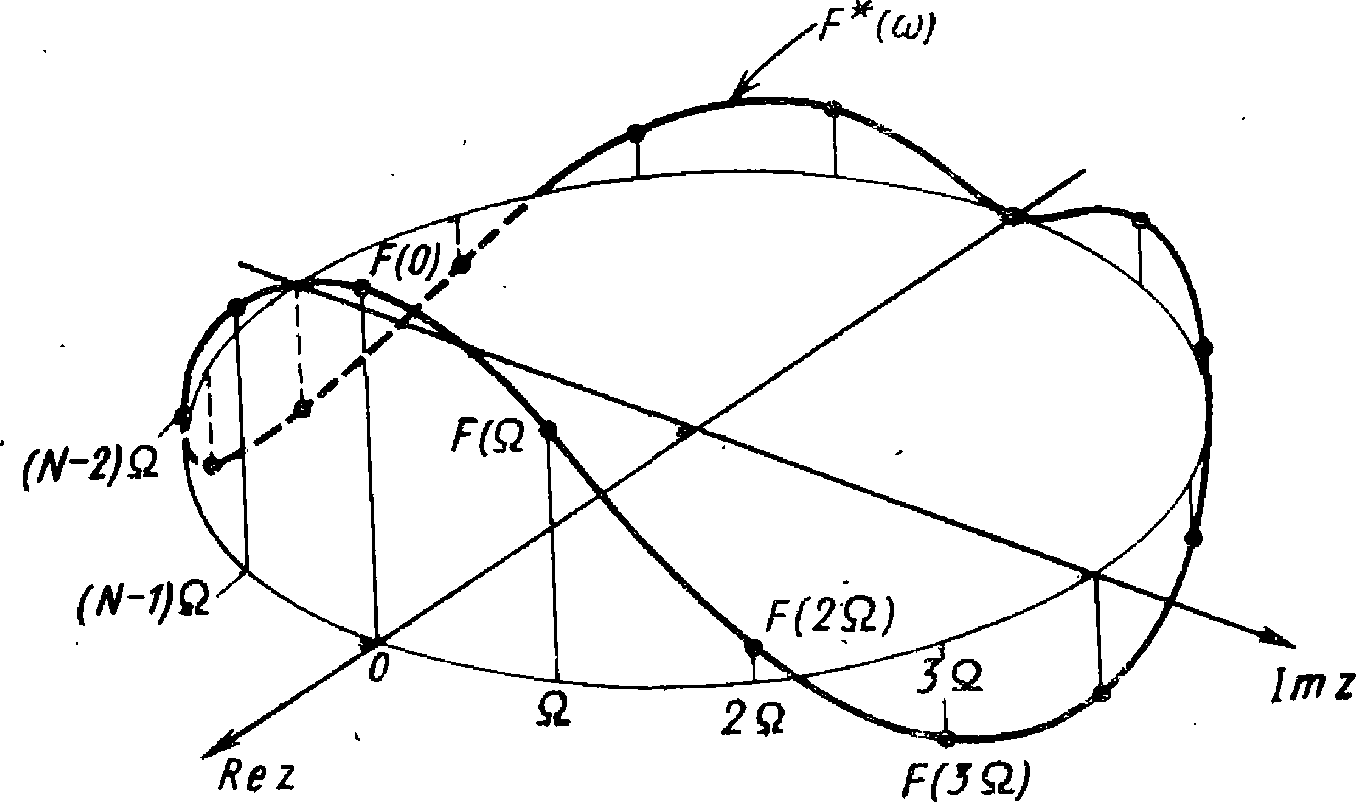
^{Рис. 5.2. Изображение периодического спектра в z-плоскости вдоль единичной окружности.}

Спектр аналоговой функции, со­стоящей из равноотстоящих импульсов, может быть по­добным же образом изображен вдоль окружности, по­скольку он периодичен по частоте.

В оставшейся части этого параграфа свойства ди­скретного преобразования Фурье будут рассмотрены бо­лее подробно. Эти свойства похожи на свойства непре­рывного преобразования Фурье. Для практического ис­пользования важно, что хотя ДПФ от последовательно­сти может только аппроксимировать преобразование Фурье от функции, свойства ДПФ являются точными, а не приближенными свойствами, основанными на ана­логии преобразований Фурье. В дальнейшем часто будет встречаться в сложных формулах выражение «х по модулю N». Поэтому, введем краткое обозначение

, (5.6)

^{Часто будет использоваться также тот факт, что:}

Дискретное преобразование Фурье от комплексной синусоиды частоты

(5. 7)

может быть выведено из определения (5.2) и будет равно:

(5.8)

где . Это сохраняет силу при любом q – целом и нецелом. В первом случае (5.8) может быть еще более упрощено. Если q – целое число, то для , так как . Для правая часть (5.8) принимает вид 0/0, поскольку , но, как легко видеть, сумма равна N. Поэтому комплексная синусоида, частота которой – целое, кратное , имеет дискретное преобразование Фурье

д ля (5.9)

для всех других ,

из которого вытекает свойство частотной селективности дискретного преобразования Фурье

ДПФ , (5.10)

тесно связанное с таким же свойством непрерывного преобразования Фурье. Однако, поскольку в ДПФ существует только N различных чисел, то только N различных частот могут быть полностью разделены. Для частот, которые не являются целыми, кратными , как видно из (5.8), все точки ДПФ будут ненулевыми.

Свойства линейности ДПФ:

(5.11)

и

, (5.12)

непосредственно вытекают из определения (5.2).

Существует обратное ДПФ – преобразование, которое приводит дискретное преобразование Фурье в последовательность, из которой оно было вычислено. Оно задается как выражение:

(5.13)

Которое отличается от (5.2) только масштабным множителем и знаком экспоненты, подобно тому, как это было в случае аналогового обратного преобразования Фурье. Для того, чтобы доказать, что (5.13) есть действи­тельно обратное преобразование, подставим (5.2) в сум­му (5.13). Это даст

,

Изменив очередность суммирований, можно вынести мно­житель за знак суммы по k. Это даст

,

где сумма по k такая же и имеет такую же форму, что и сумма (5.8). Внутренняя сумма равна N для ((l))=n и нулю во всех остальных случаях. Таким образом, только одно слагаемое внешней суммы отлично от нуля, и (5.13) доказано.

Обратное ДПФ подобно ДПФ может давать отсчеты f(lТ) для l вне интервала , но эти отсчеты есть просто повторение .значений f(lТ) для l, взятых вну­три этого интервала. Поэтому можно представить значе­ния f(lТ) расположенными вдоль окружности или же периодически продолженными.

Рассмотрим теперь обратное дискретное преобразова­ние Фурье от произведения дискретных преобразований Фурье, для которого соответствующим аналоговым ре­зультатом является свертка. Таким образом, рассмотрим

(5.14)

где и являются ДПФ последовательностей х(пТ) и у(пТ) соответственно. Предполагается, конечно, что и х(пТ) и у(пТ) имеют равное число точек N. Для того чтобы оценить (5.14), подставим определения и :

(5.15)

Это выражение можно записать как тройную сумму по k, т и п. Если изменить порядок суммирования таким образом, чтобы сумма по к стала самой внутренней, то можно х(пТ)у(тТ) вынести из под знака этой суммы и получить

(5.16)

Сумма в скобках теперь имеет тот же вид, что и в двух предыдущих доказательствах, и равна нулю для всех т и п, за исключением комбинации т и п, удовлетво­ряющей условию

; (5.17)

для которой сумма в скобках равна N. Таким образом, (5.16) сводится к выражению

(5.18)

в котором для простоты применены обозначения переменных с помощью индексов. Таким образом, показано, что произведение дискретных преобразований Фурье есть дискретное преобразование Фурье от круговой свертки. Смысл выражения (5.18) иллюстрируется рис. 5.3, где последовательность х(пТ) с пятью точками, обозна­ченная через х_п, циклически свертывается с последова­тельностью у_m также с пятью точками. Можно рассмат­ривать одну или обе последовательности как периодиче­ски продолжающиеся (светлые точки) или же можно рассматривать их расположенными .вдоль окружности. На линии 1, рис. 5.3, показана последовательность х_п, а на линии 2 — периодически продолженная последова­тельность у_п. На линии 3, представляющей сверточную сумму , последовательность у перевернута по времени и умножается на соответствующий член последователь­ности х. На линиях с 4 по 7 показано, как сдвигается пе­ревернутая по времени последовательность у для вычисления , , и . Когда отсчет у_т выдвигается из ин­тервала вправо, тот же отсчет вдвигается в диапазон с левой стороны.

Рис. 5.3 иллюстрирует, почему круговая свертка иног­да называется периодической. В противоположность это­му соответствующее свойство непрерывного преобразова­ния Фурье может быть названо апериодической сверткой.

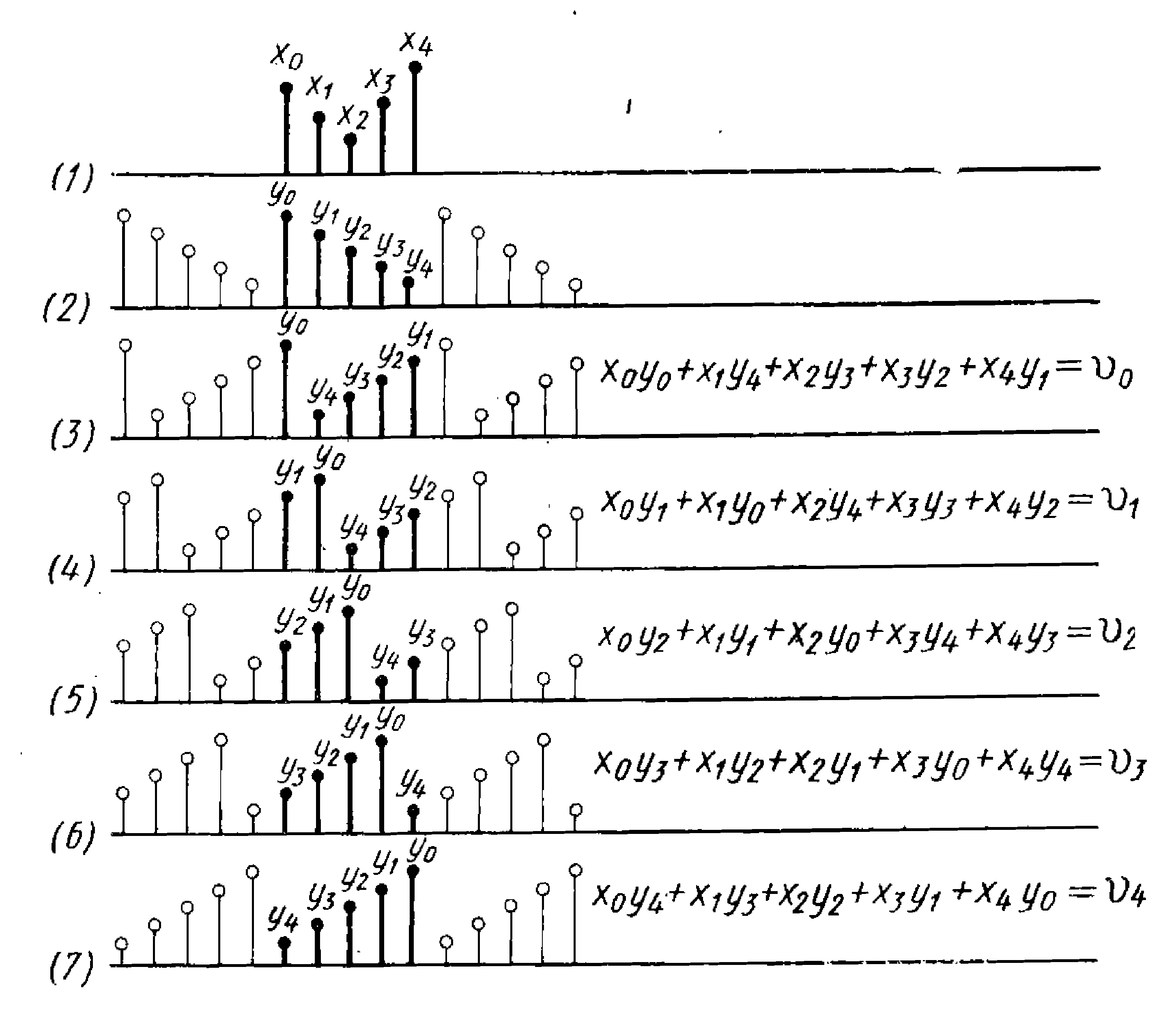
Рис. 5.3. Периодическая или круговая свертка

В большинстве задач, где используется свертка, имеется в виду апериодическая свертка. Естественным следствием из теоремы о круговой cвертке является теорема кругового смещения:

, (5.19)

которая устанавливает, что перемещение l отсчетов из конца последовательности в ее начало эквивалентно ум­ножению дискретного преобразования Фурье на линейно-фазовую функцию. Это аналогично непрерывному преоб­разованию Фурье от функции, сдвинутой по времени.

Некоторые свойства дискретного преобразования Фурье связаны с нечетными и четными последовательно­стями. Нечетная последовательность из N отсчетов, х(пТ) определяется как

(5.20)

а четная последовательность из N отсчетов, у(пТ), — как

(5.21)

Если последовательности изображены вдоль окружно­сти или периодически продолжены, то эти определения весьма похожи на аналогичные определения нечетных или четных функций. Это иллюстрируется рис. 5.4,а, на котором изображена чет­ная последовательность из шести отсчетов, и рис. 5.4,б, на котором изобра­жено периодическое продолжение рис. 5.4,а.

Четная последователь­ность с действительными отсчетами имеет дискрет­ное преобразование Фу­рье, которое также явля­ется действительным и четным. Нечетная после­довательность с действи­тельными отсчетами имеет дискретное преобразова­ние Фурье, которое явля­ется нечетным и чисто мнимым. Любая действительная по­следовательность имеет преобразование, действительная часть которого является четной, а мнимая часть — нечет­ной.

Рис. 5.4. Четная последователь­ность (а), ее периодическое про­должение (б).

Преобразование четной, но не чисто действительной последовательности будет также четным, но не чисто дей­ствительным, а преобразование последовательности, ко­торая является нечетной, но не чисто мнимой будет нечетным и не чисто действительным. Эти и другие по­добные свойства сведены в табл. 5.1. Благодаря симмет­рии определений прямого и обратного преобразований таблица останется в силе, если заголовки столбцов f(пТ) и F(kΩ) поменять местами.

Таблица 5.1

f(пТ)		F(kΩ)
Четная Нечетная Четная и действительная Нечетная и действительная Действительная Мнимая Четная и мнимая Нечетная и мнимая		Четная Нечетная Четная и действительная Нечетная и мнимая Действительная часть четная, мнимая часть нечетная Действительная часть нечетная, мнимая часть четная Четная и мнимая Нечетная и действительная

Теперь рассмотрим свойства дискретных преобразова­ний Фурье, от искусственно удлиненных последователь­ностей. Так, допустим, что имеются отсчеты f(пТ), , и создается более длинная последователь­ность g(пТ), , r – любое целое число и где

(5.22)

В определении ДПФ от g(пТ) необходимо потреблять вместо :

(5.23)

Если k делится на r, то

(5.24)

Если k не делится на r или если r не является целым числом, то значения G отличаются от значений F, но между ними может быть установлена связь, если учесть, что обе последовательности значений являются отсчета­ми одной и той же непрерывной функции , только расположение отсчетов по часто­те у них разное.

Другим способом искусственного удлинения последо­вательности является ее повторение. Предположим, что имеется последовательность h(пТ) с rN точками, задан­ная как

для (5.25)

Для h(пТ) ДПФ определяется следующим образом:

(5.26)

которое можно записать так:

(5.27)

где . Сумма по l есть уже знакомая сумма (5.8), так что

(5.28)

Несколько интересных и важных теорем связывают ДПФ последовательности f(пТ) с ДПФ последователь­ности, состоящей из тех же членов, что и f(пТ), но пере­ставленных местами. Выше уже рассматривалось влия­ние одного вида перестановки, а именно вращения, в (5.19). Рассмотрим теперь ДПФ переставленной последовательности (для того, чтобы показать, что (5.29) есть действительно пе­рестановка, необходимо доказать однозначное соответствие целых чисел от 0 до N—1 и последовательности ((рп)), . По­скольку , достаточно показать, что во всех случаях, за исключением . Если предположить обрат­ное для некоторых и тогда должно быть сравнимо с нулем по модулю N и поэтому имеет множитель N. Поскольку р не имеет множителем N. то должно быть кратным N. Но , и поэтому , что противоречит предположению. Следовательно, существует однозначное соответствие, и (5.29) дей­ствительно есть перестановка):

, (5.29)

где р — целое число, не имеющее общих делителей с N. ДПФ от g(пТ) имеет вид:

(5.30)

Предположим теперь, что найдено единственно целое q (в пределах ), причем такое, что

(5.31)

(Решение (5.31) должно существовать, поскольку доказано в предыдущей сноске, что ((рп)) принимает все значения от 0 до N—1. Поэтому некоторые п дают ((рп)) = 1).

Произведем замену индекса:

, (5.32)

в (5.30), тогда получим

(5.33)

Уравнение (5.33) устанавливает, что перестановка чле­нов последовательности согласно

до вычисления ДПФ эквивалентна перестановке членов ДПФ согласно

(Не всегда ясно, как решить сравнение (5.31) для q. Бренне­ром была предложена следующая модификация алгоритма Евклида. Образуем две последовательности и , приняв , , , , и . Будем повторять это до тех пор, пока не станет равно нулю и не ста­нет равно q).

Частным случаем (5.33) будет случаи, когда , для которого

(5.34)