
- •Часть 1
- •1. Линейная алгебра
- •1.1. Основные классы квадратных матриц
- •Задачи для самостоятельного решения
- •1.2. Определители. Ранг матрицы
- •1.2.1. Вычисление определителей
- •1.2.2. Вычисление ранга матриц
- •Задачи для самостоятельного решения
- •1.3. Обратная матрица
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Как изменится матрица , если совершить аналогичные преобразования со столбцами матрицы а?
- •1.4. Жорданова нормальная форма
- •1.5. Возведение матриц в степень. Нильпотентные матрицы. След матрицы
- •Задачи для самостоятельного решения
- •1.6. Многочлены
- •Задачи для самостоятельного решения
- •2. Введение в анализ
- •2.1. Метод математической индукции
- •Алгоритм метода математической индукции
- •Решение. Используем метод математической индукции.
- •Задачи для самостоятельного решения
- •2.2. Пределы последовательностей
- •Упражнение 14. Найти
- •Примеры решения задач
- •Пример 2. Пусть , . Найти .
- •Задачи для самостоятельного решения
- •1. Вычислить пределы:
- •2.3. Предел функции. Непрерывность
- •Примеры решения задач
- •Пример 8. Доказать, что если функция непрерывна на отрезке и имеет обратную функцию, то она монотонна на этом отрезке.
- •Задачи для самостоятельного решения
- •3.1. Производная функции. Вычисление производной по определению
- •Если он существует и конечен, называется правосторонней (левосторонней) производной и обозначается . Если существует производная , то будем говорить, что дифференцируема в точке .
- •Теорема 2. Если существует производная , то функция непрерывна в точке .
- •Примеры решения задач Пример 1. Пусть Подобрать коэффициенты a и b так, чтобы функция была дифференцируемой в точке .
- •Заметим, что как произведение бесконечно малой функции на ограниченную , после замены получим
- •Задачи для самостоятельного решения
- •1. Показать, что функция , где – непрерывная функция и , не имеет производной в точке .
- •2. Пусть
- •3.2. Вычисление пределов функций с использованием методов дифференциального исчисления
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •1. Вычислить пределы
- •3.3. Выпуклые и вогнутые функции. Точки перегиба
- •Важную роль при исследовании функции на выпуклость вверх (выпуклость вниз) играют точки, в которых происходит изменение направления выпуклости функции.
- •В этом разделе будут рассмотрены основные свойства выпуклых вниз (вверх) функций, заданных на отрезке .
- •Задачи для самостоятельного решения
- •3.4. Основные теоремы дифференциального исчисления
- •Примеры решения задач
- •Обратим внимание на то, что является точкой перегиба функции . Оказывается, что этот факт верен для любой дважды дифференцируемой функции.
- •Так как , то , что и требовалось доказать.
- •Задачи для самостоятельного решения
- •6. Исследование функции нескольких переменных на экстремум
- •7. Доказательство тождеств с использованием свойств дифференцирования
- •Задачи для самостоятельного решения
- •3.6. Производные высших порядков
- •Задачи для самостоятельного решения
- •Заключение
- •Часть 1
- •394006 Воронеж, ул. 20-летия Октября, 84
1.5. Возведение матриц в степень. Нильпотентные матрицы. След матрицы
В начале этого раздела рассмотрим различные способы возведения матрицы в степень.
Первый способ
основан на представлении матрицы А в
виде
![]() ,
где J – жорданова
форма А, и на использовании формулы
,
где J – жорданова
форма А, и на использовании формулы
![]() и формулы для
и формулы для
![]() из упражнения 5 предыдущего раздела.
из упражнения 5 предыдущего раздела.
Упражнение
1. Вычислить
![]() ,
где
,
где
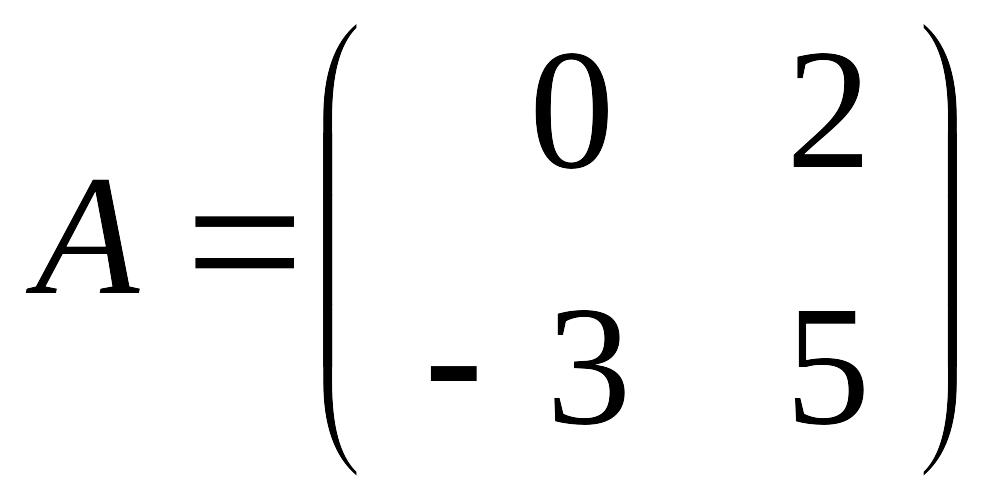 .
.
Решение. Найдем собственные значения матрицы А, т.е. решения уравнения .
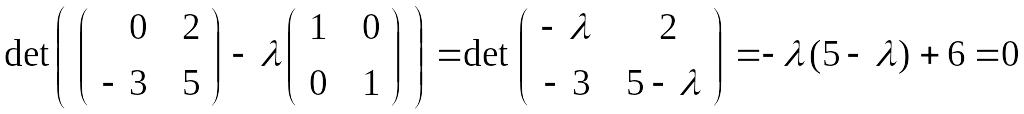 .
.
Отсюда
![]() .
По теореме Жордана найдется матрица Т
такая, что выполнено равенство
.
По теореме Жордана найдется матрица Т
такая, что выполнено равенство
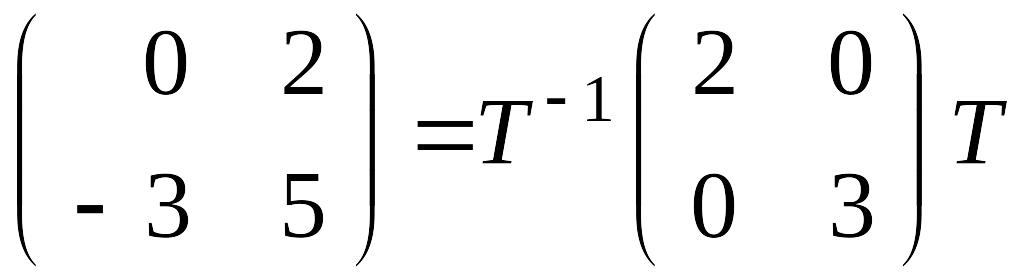 ,
или, что то же самое,
,
или, что то же самое,
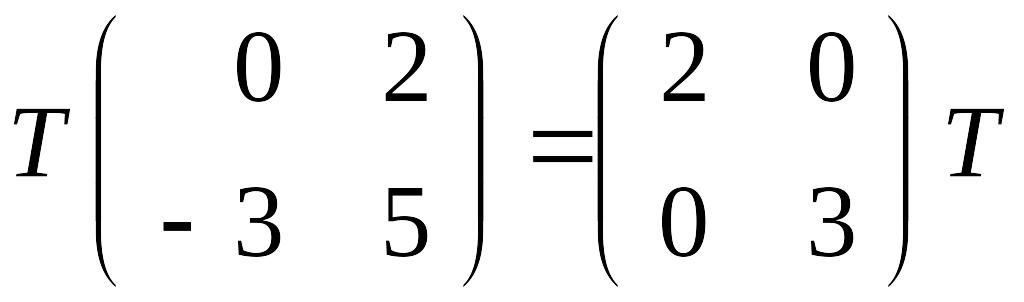 .
Определим матрицу Т. Пусть
.
Определим матрицу Т. Пусть
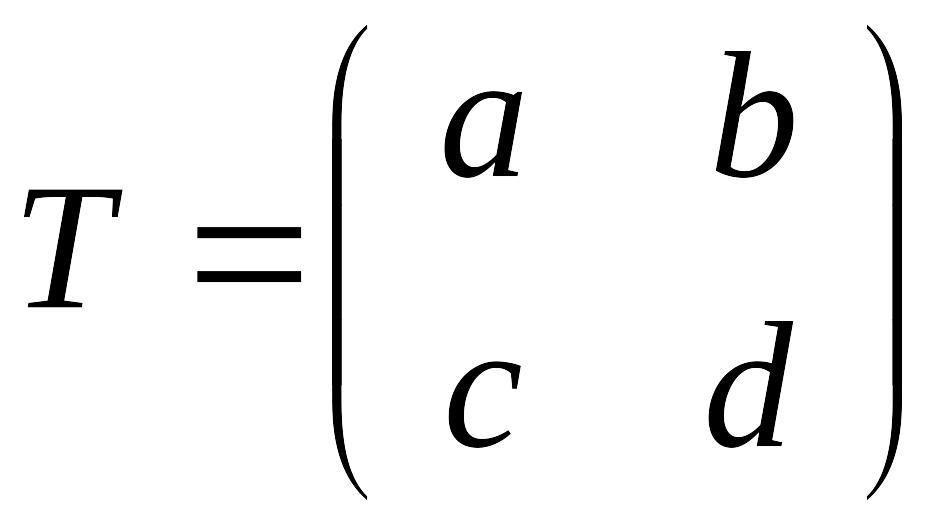 .
Тогда матричное уравнение
.
Тогда матричное уравнение
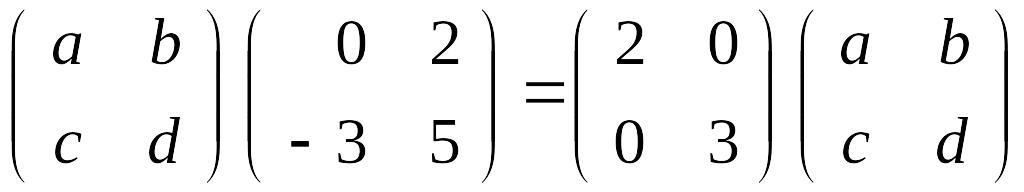
приводит к системе
![]()
одним из решений которой будет
![]()
Отсюда
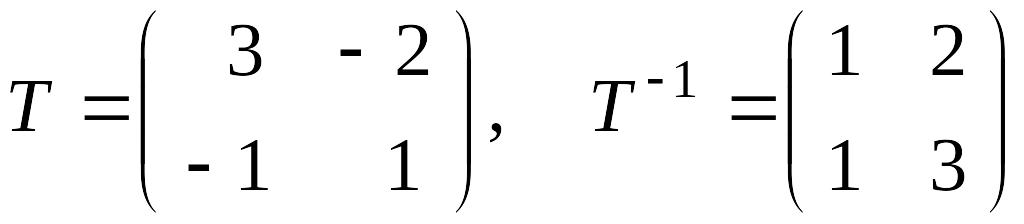 и
и
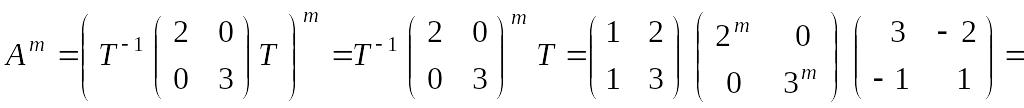
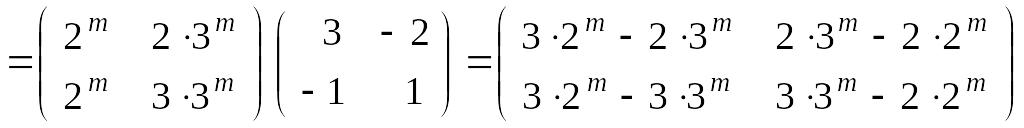 .
.
Второй
способ. Индуктивный метод вычисления
![]() .
Этот метод основан на вычислении
нескольких первых степеней матрицы А,
установлении закономерностей изменения
элементов
и строгом доказательстве методом
математической индукции.
.
Этот метод основан на вычислении
нескольких первых степеней матрицы А,
установлении закономерностей изменения
элементов
и строгом доказательстве методом
математической индукции.
Упражнение
2. Вычислить
,
где
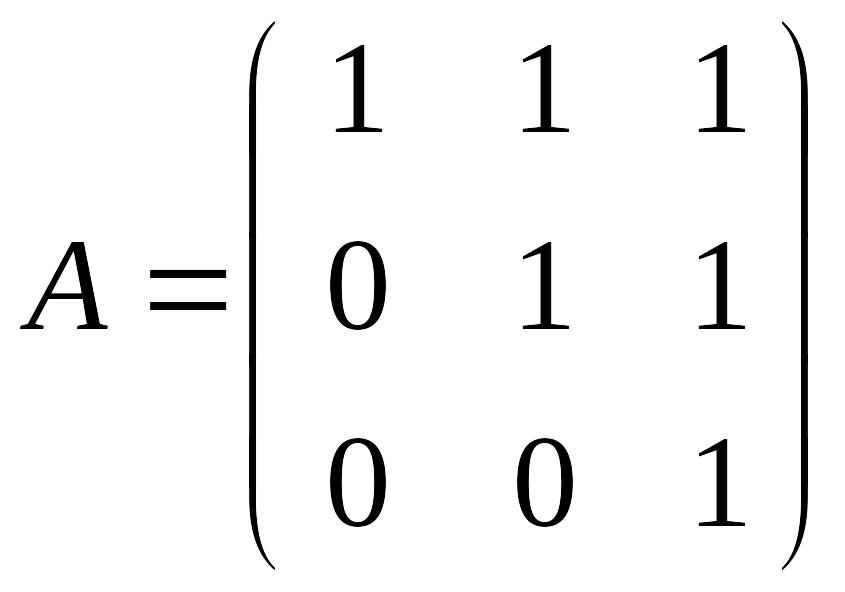 .
.
Решение.
Для начала вычислим
![]()
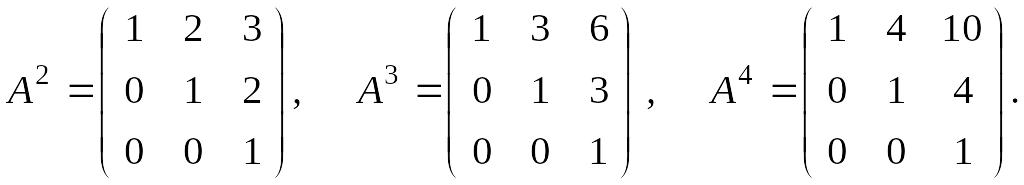
Заметим, что
элементы главной диагонали равны 1.
Элементы над главной диагональю совпадают
со степенью матрицы А, а для элемента
![]() матрицы
при m = 2, 3, 4 выполнено
равенство
матрицы
при m = 2, 3, 4 выполнено
равенство
![]() .
.
Теперь мы можем сделать индуктивное предположение
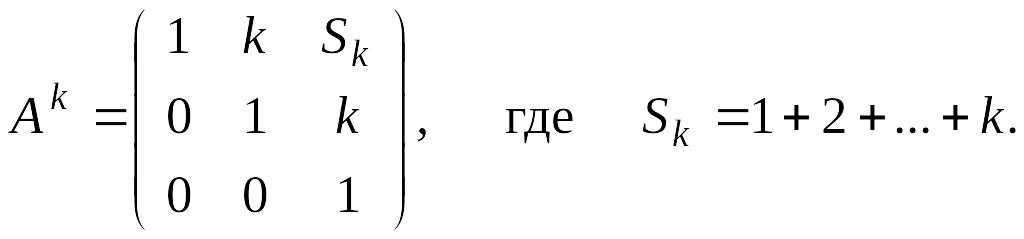
Покажем, что
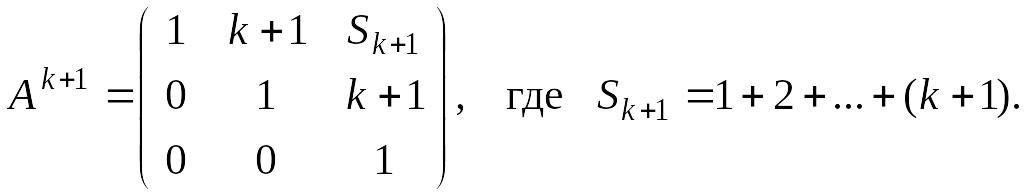
Действительно,

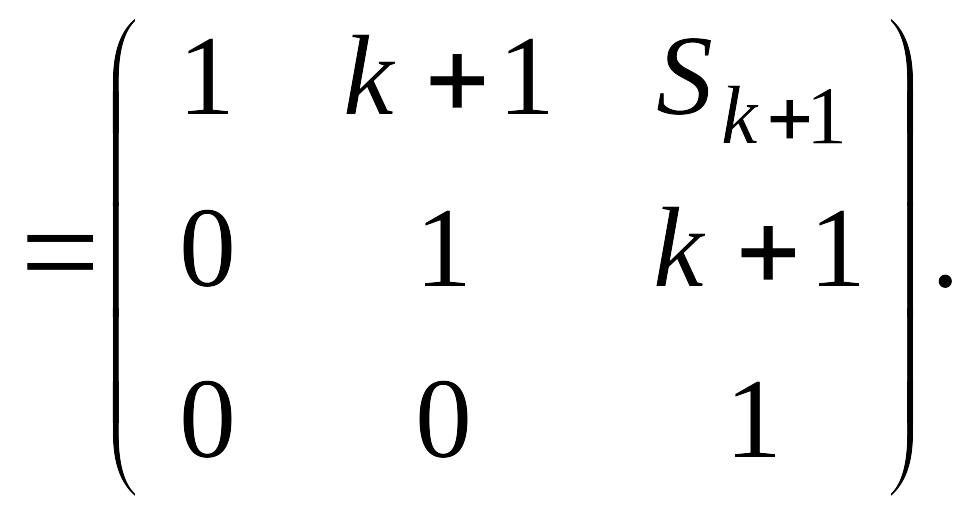
Что и требовалось доказать. Это означает, что
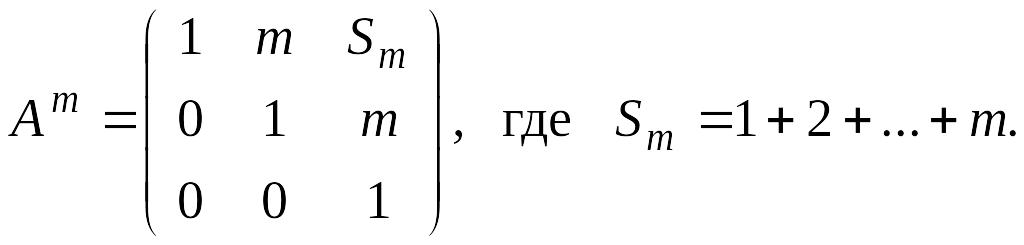
Третий способ основан на применении матричного аналога формулы бинома Ньютона.
Теорема 1. Если матрицы А и В перестановочны (то есть выполнено равенство АВ = ВА), то
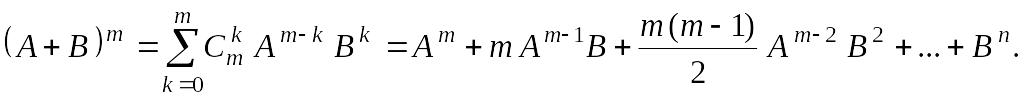
Если матрица
B в условии теоремы 1
нильпотентна (то есть
![]() для не-которого
для не-которого
![]() ),
то для всех
),
то для всех
![]() верна формула
верна формула
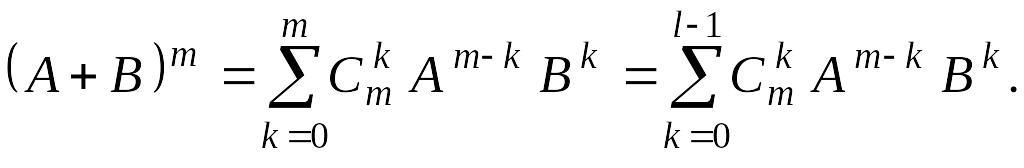
Фактически мы
уже пользовались этим результатом при
нахождении степеней жордановой клетки
![]() при решении упражнения 5.
при решении упражнения 5.
Применим формулу бинома Ньютона для решения упражнения 2 раздела 1.5. Запишем А в виде суммы перестановочных матриц:
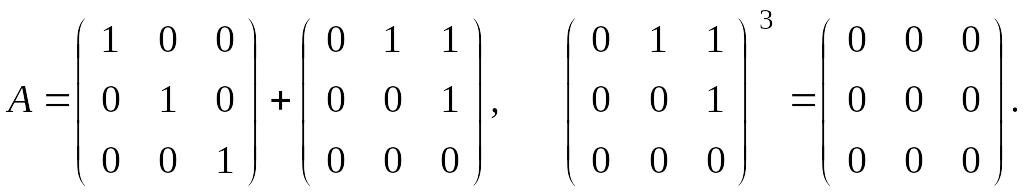
Таким
образом, для
![]() получаем
получаем
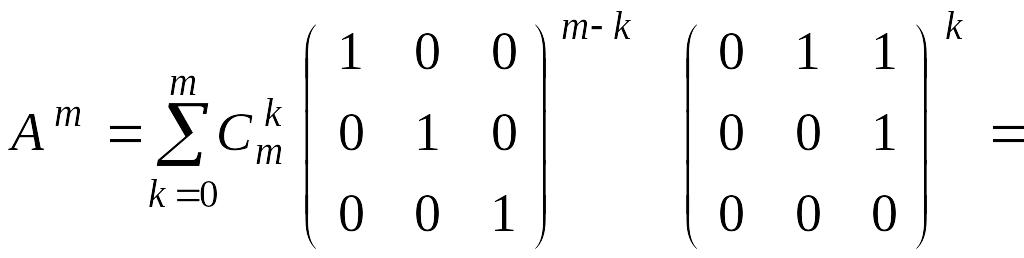
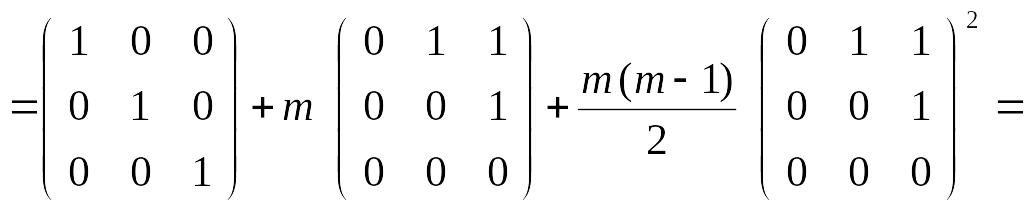
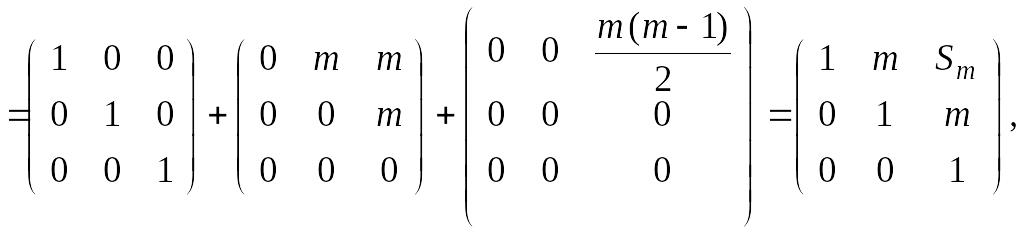
где
![]() согласно формуле суммы m
первых членов арифметической прогрессии
1, 2, 3, … .
согласно формуле суммы m
первых членов арифметической прогрессии
1, 2, 3, … .
Для
m = 2 матрица
![]() вычисляется непосредственно.
вычисляется непосредственно.
Замечание.
Отметим, что использование первого
способа не всегда оправдано для матриц
больших размерностей, так как для
вычисления элементов матрицы T
уже при n = 4 требуется
решать систему из 16 уравнений. С другой
стороны, применение второго и третьего
способов затруднительно для вычисления
степеней простейших матриц второго
порядка типа
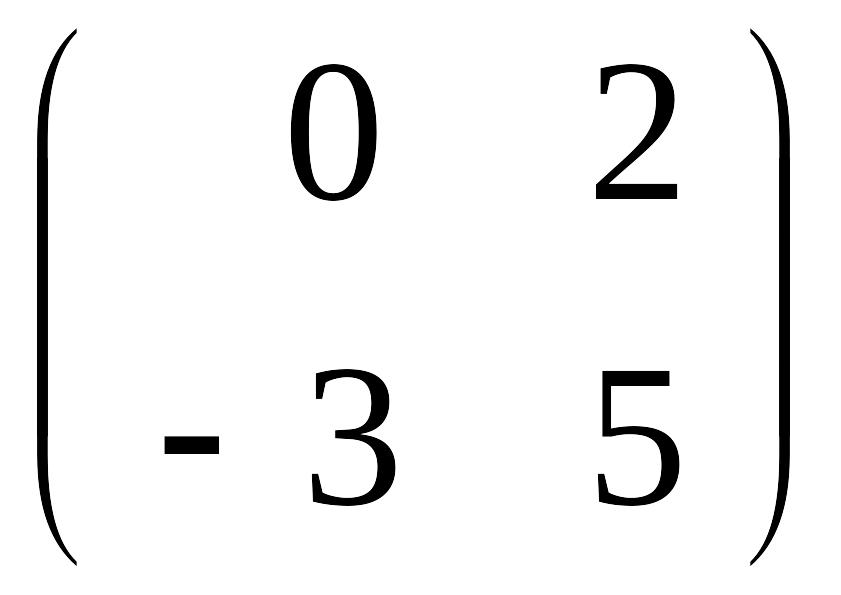 (предлагаем читателям проверить это
самостоятельно).
(предлагаем читателям проверить это
самостоятельно).
Определение
1.
Следом квадратной матрицы А
назы-вается сумма элементов главной
диагонали и обозначается![]() .
.
Лемма..
Пусть А и В – квадратные матрицы
порядка n. Тогда
выполнено равенство
![]() .
.
Доказательство. Используем метод математической индукции.
1. Для n = 2 утверждение проверяется непосредственно.
2.
Предположим, что утверждение верно для
некоторого
![]() .
.
3.
Покажем, что оно верно для
![]() .
.
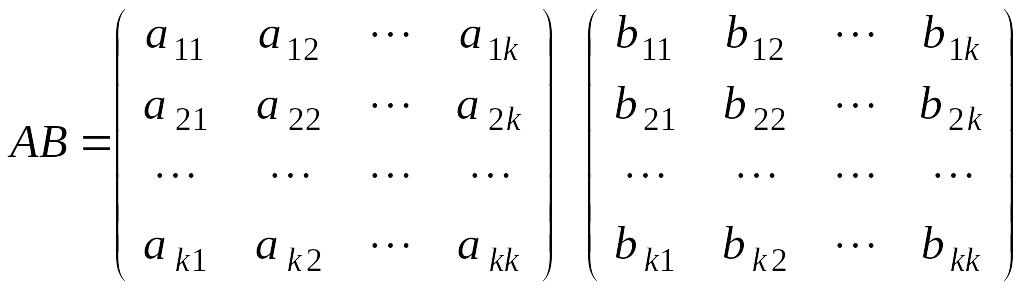 .
.
Обозначим строки и столбцы матриц и следующим образом:
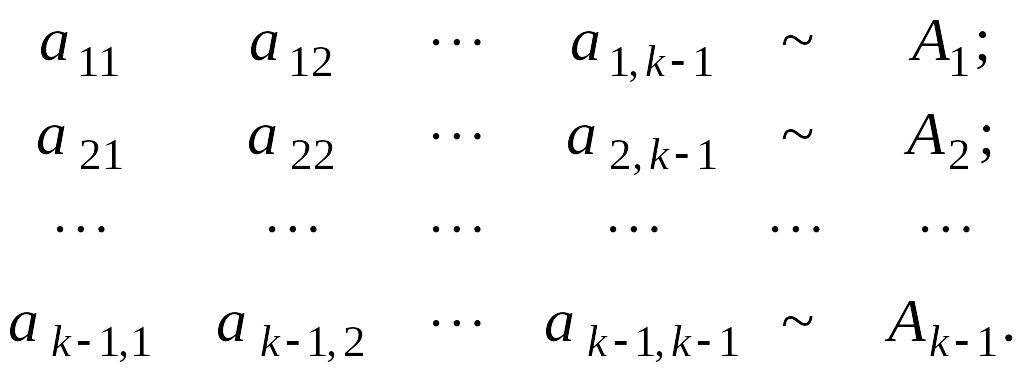
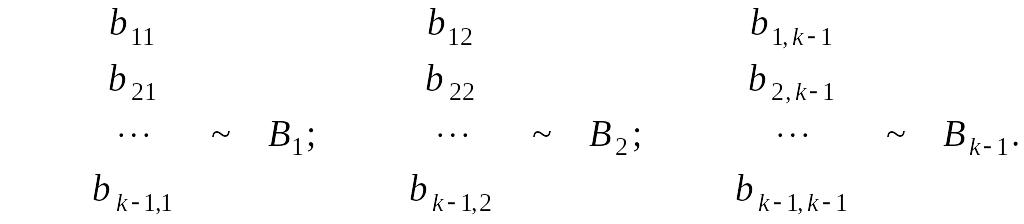
![]()
Тогда
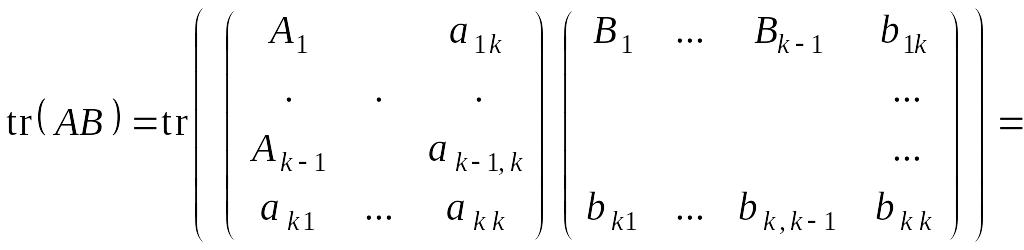
![]()
![]()
Аналогично
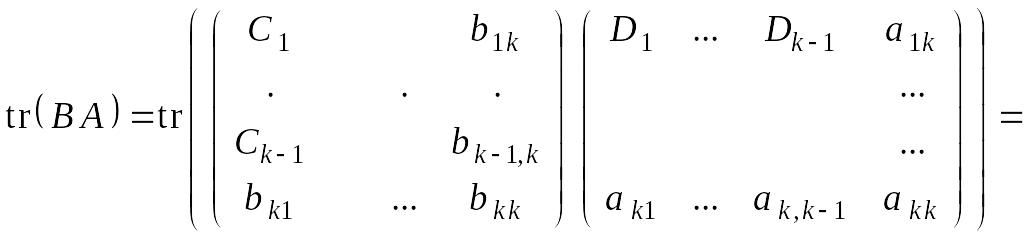
![]()
![]()
Заметим,
что
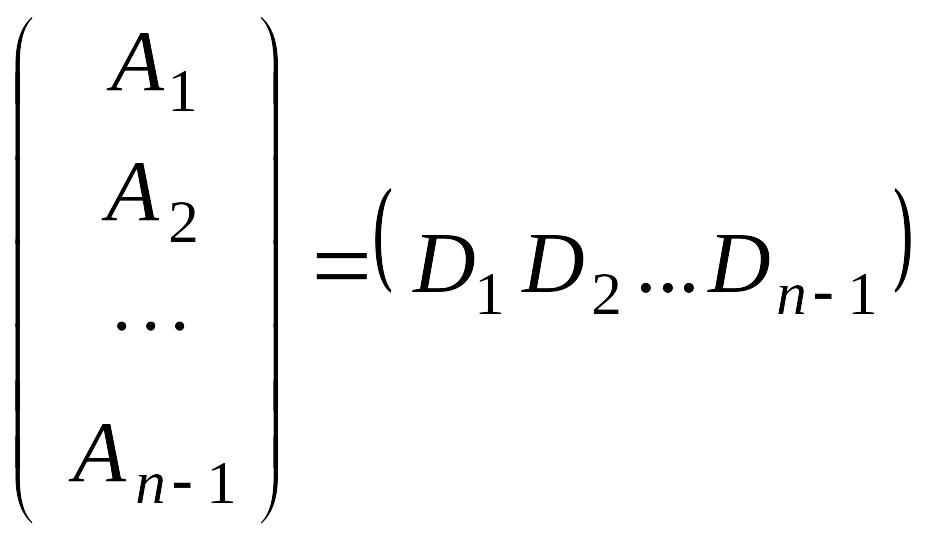 и
и
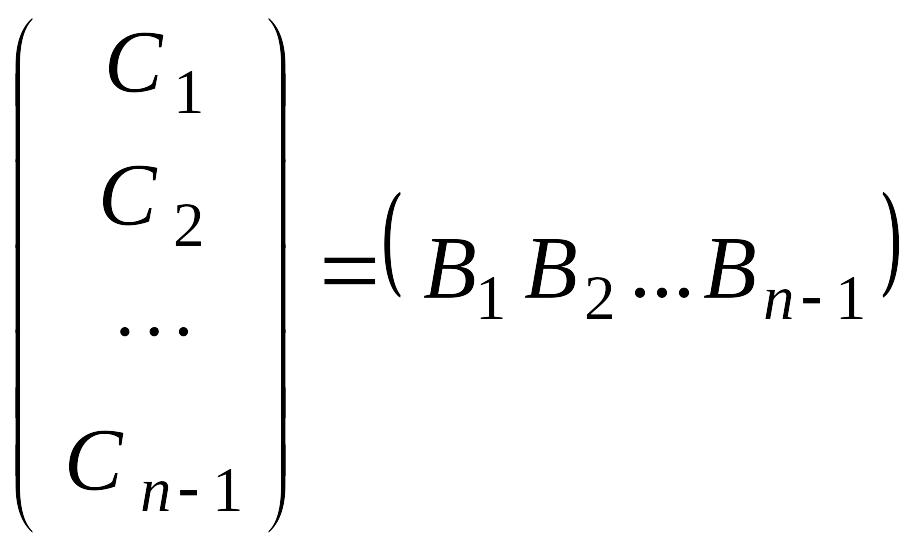
– матрицы порядка n – 1 и
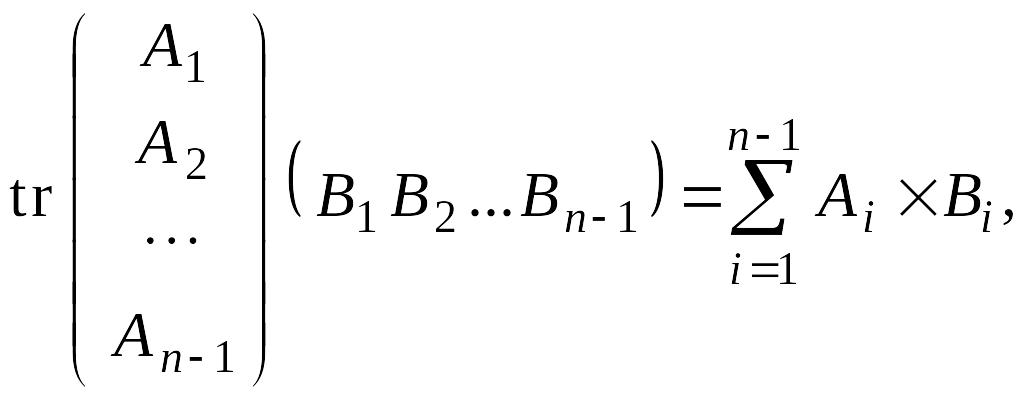
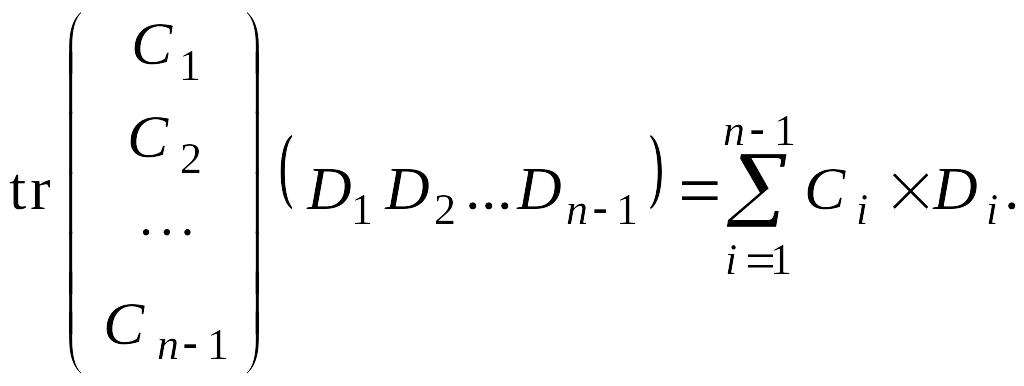
В силу индуктивного
предположения 2
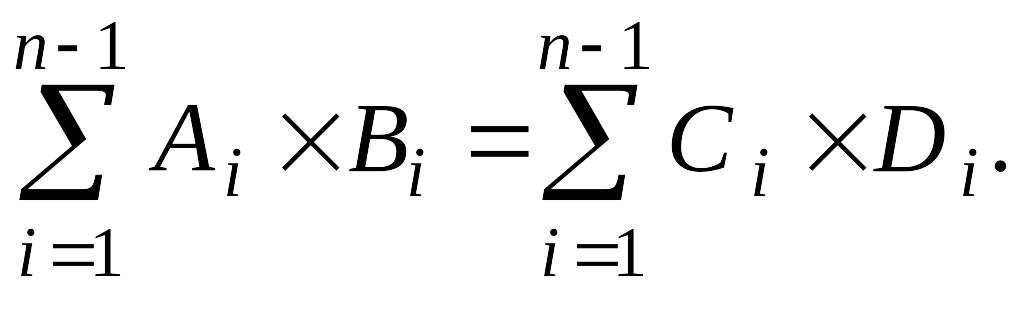 Отсюда следует равенство
Отсюда следует равенство
![]() .
.
Упражнение
3. Пусть А – матрица размерности
![]() ,
причем
,
причем
![]() .
Вычислить
.
Вычислить
![]() ,
где
,
где
![]() .
.
Решение.
Пусть
–
жорданова форма матрицы А и
![]() –
ее собственные значения, тогда
–
ее собственные значения, тогда
![]()
Так
как
![]() – верхняя треугольная матрица и на ее
главной диагонали стоят элементы
– верхняя треугольная матрица и на ее
главной диагонали стоят элементы
![]() то
то
![]()
![]()
Значит,
![]()
![]() согласно задаче 14 (см. задачи для
самостоятельного решения ниже) ,
согласно задаче 14 (см. задачи для
самостоятельного решения ниже) ,
![]()
Итак,
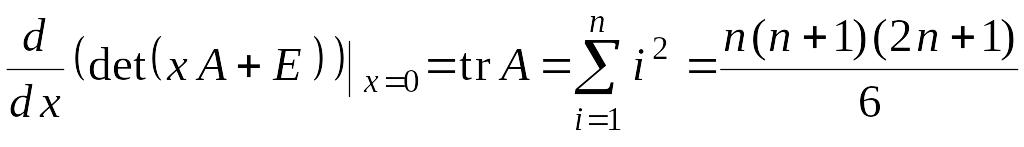 .
.
Последнее равенство доказано в примере 1 пункта 3.
