Примеры решения задач
Пример 1.
Вычислить
для
.
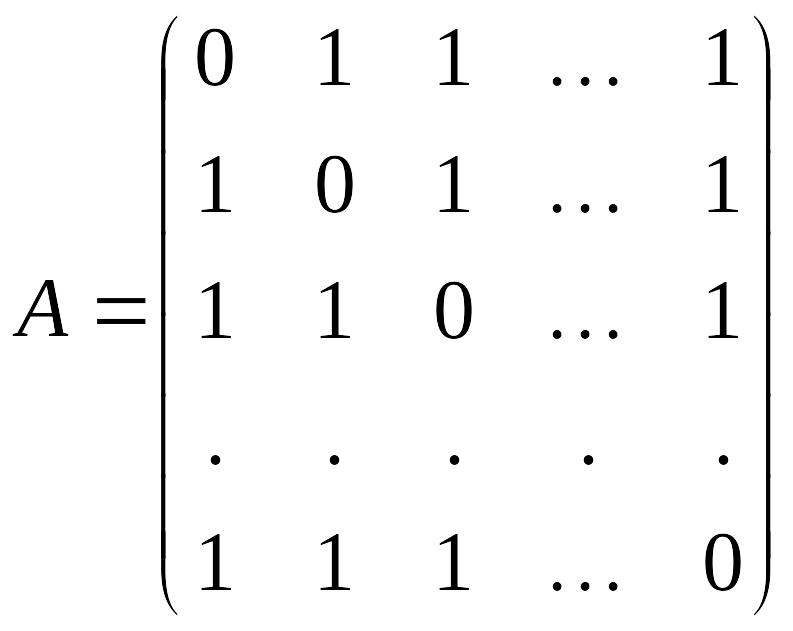Решение. Обозначим
.
Из
равенства
и правила умножения матриц получаем
систему для нахождения
:
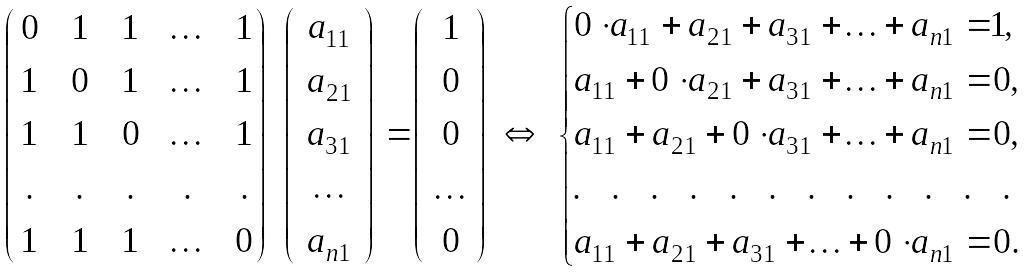
Вычитая
из второго уравнения третье, из третьего
– четвертое и, наконец, из (n–1)-го
уравнения n-е уравнение
получаем
.
Теперь из первого уравнения получаем
,
из второго –
.
Аналогично
вычисляем элементы матрицы, состоящие
в остальных столбцах, и получаем
,
если
,
.
Таким образом,
.
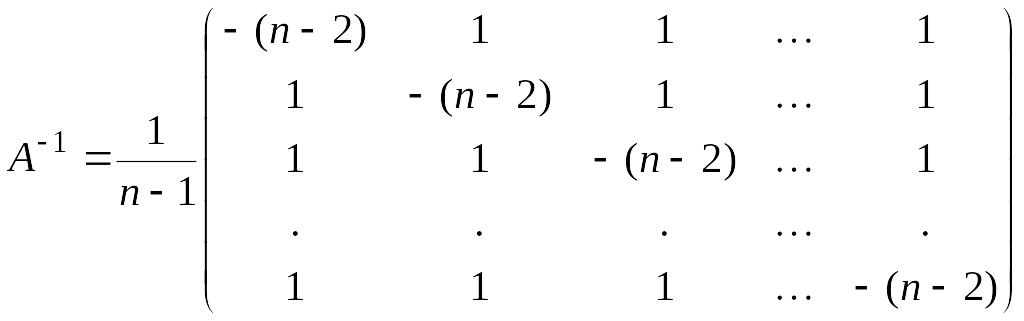Пример 2. Вычислить для
.
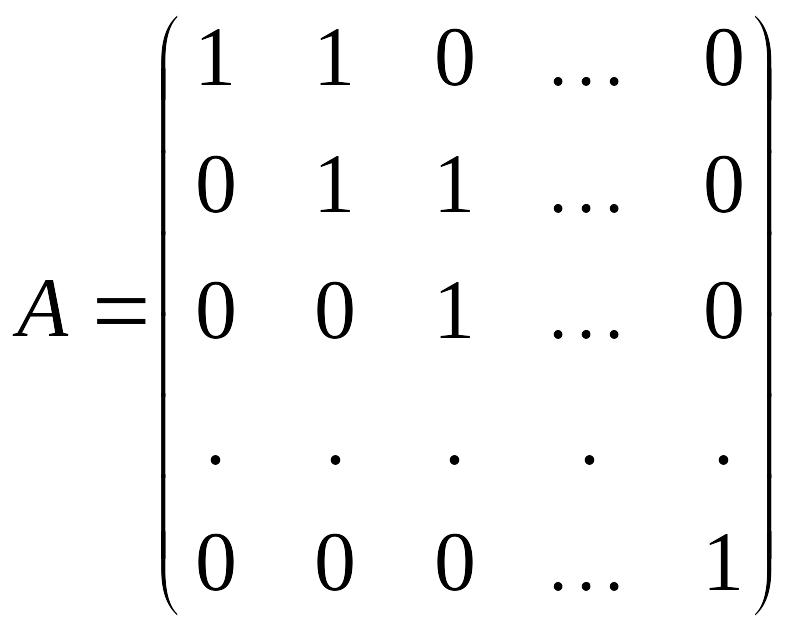Решение.
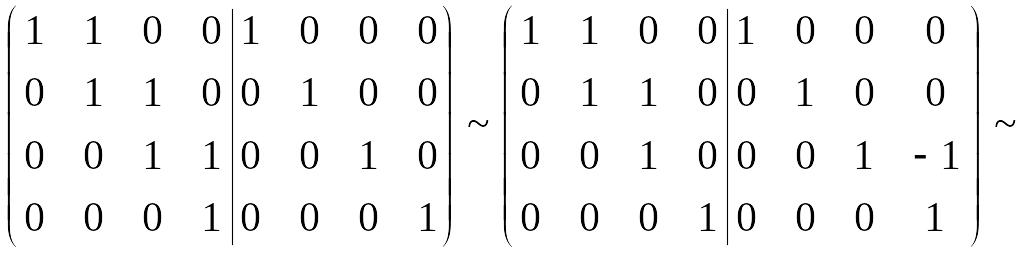
Используем метод элементарных
преобразований. Проиллюстрируем этот
метод для матрицы порядка 4. Построим
матрицу
размерности
и преобразуем ее следующим образом: из
третьей строки вычтем четвертую и
результат запишем вместо третьей строки,
затем из второй получившуюся третью и
из первой получившуюся вторую. В итоге
получим матрицу
,
где
.
.
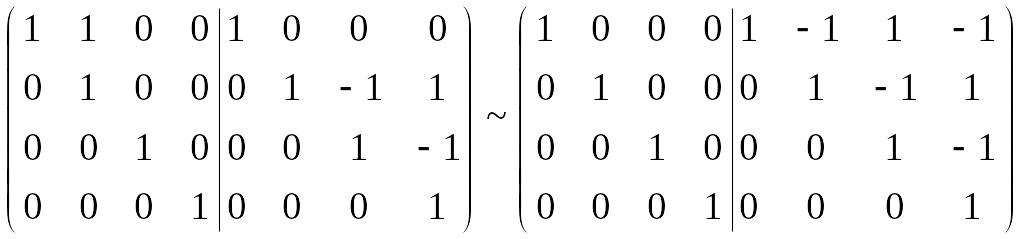Таким
образом,
.
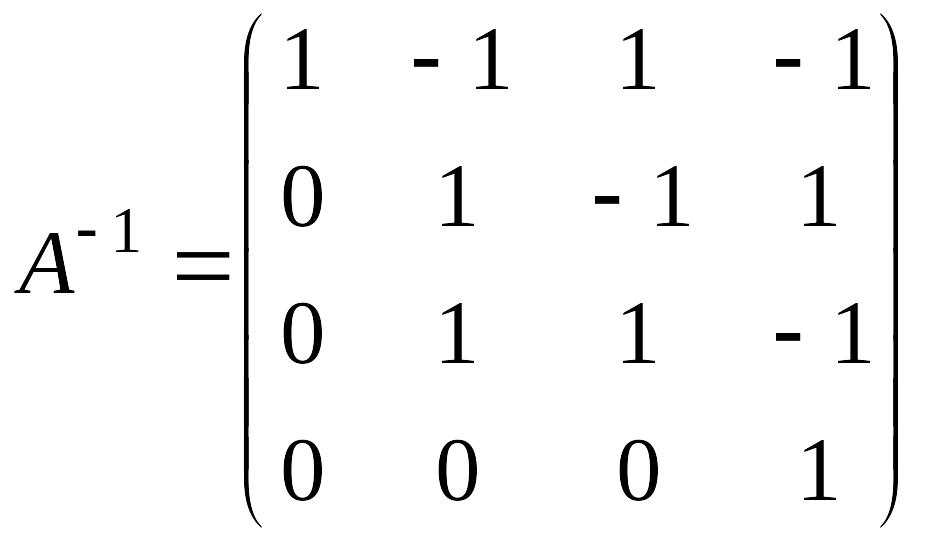Очевидно, что описанный метод безо всяких изменений применим в общем случае и дает следующий результат:
.
Пример
3.
Доказать, что если матрица
обратима, то матрица
также обратима.
Решение.
Первый
способ.
Предположим, что матрица
необратима, тогда найдется вектор
такой, что
.
В этом случае
Так
как
– обратимая матрица, то
.
Отсюда получаем, что
что противоречит нашему предположению.
Второй способ. Непосредственной проверкой убедиться, что
Пример
4. Найти
матрицу, обратную
,
где А
и С
–обратимые матрицы одного порядка.
Решение.
Первый
способ.
Иногда (в частности, и в этом случае)
бывает удобно начинать решение задачи
с рассмотрения простейшего частного
случая. Для начала будем считать, что
А,
В,
С
– матрицы первого порядка, то есть
обыкновенные числа, причем
и
.
Тогда
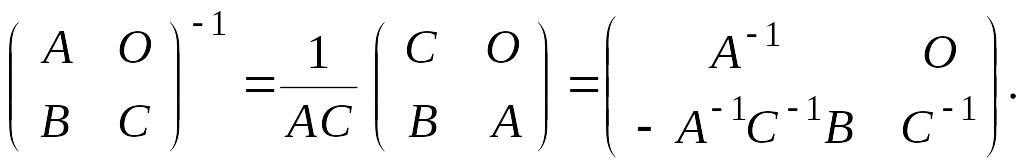
При переходе к
общему случаю нужно обратить внимание
на выбор порядка множителей
,
так как умножение матриц, в отличие от
умножения чисел, – некоммутативная
операция. Путем несложного перебора
убеждаемся, что
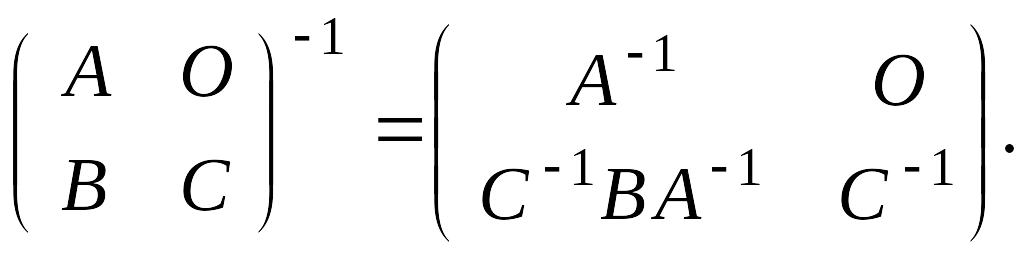Действительно,
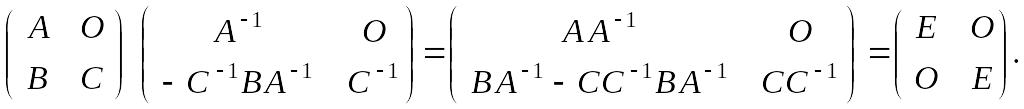
Второй
способ. Пусть
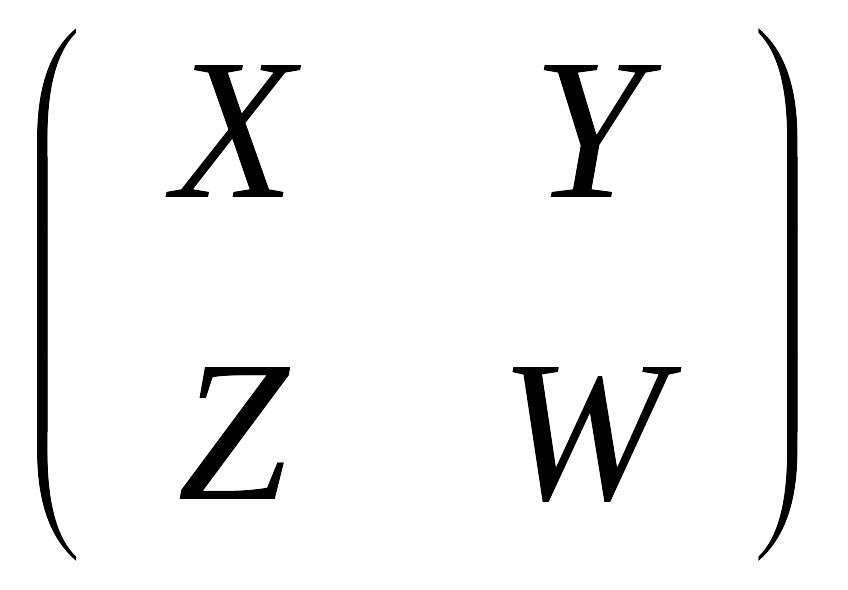– искомая матрица. Тогда
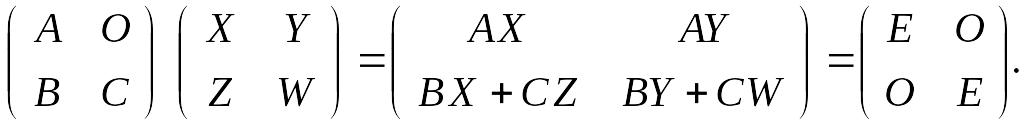
Отсюда получаем четыре матричных уравнения
Так как А
обратима, то
и
.
Так как С
обратима, то
Таким образом,
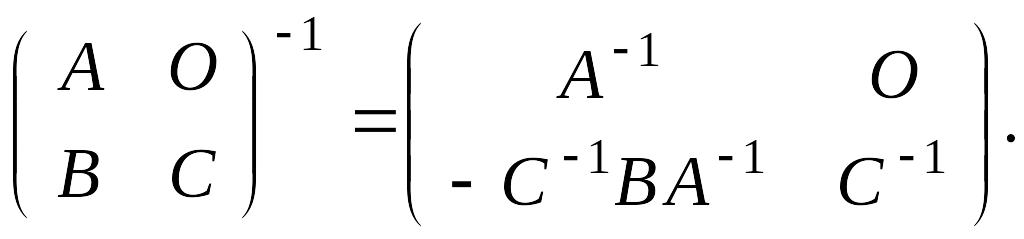
Пример
5.
Пусть А – обратимая матрица
порядка n. Доказать,
что
обратима
и
.
Решение.
Возьмем два произвольных вектора
и рассмотрим их скалярное произведение:
(согласно утверждению 2 раздела 1.1)
Отсюда следует, что
Так как x
– произвольный вектор, то можем
сделать подстановку
,
которая приводит к равенству
Так как модуль вектора равен нулю, только если этот вектор нулевой, то получаем равенство
Так как y –
произвольный вектор из
то последнее равенство верно только в
случае, когда матрица
–
нулевая, то есть
.
По определению обратной матрицы это
означает, что
.
Задачи для самостоятельного решения
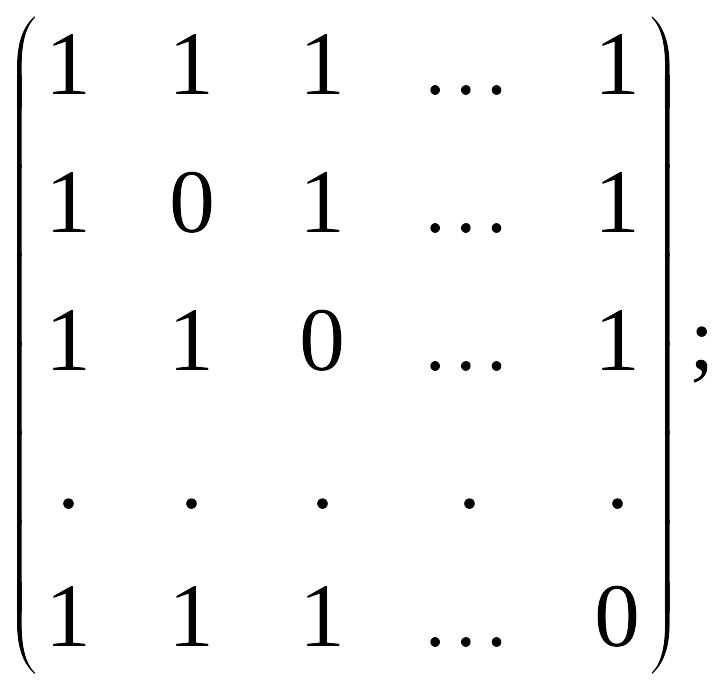
1.Найти обратные матрицы для следующих матриц:
а)
б)
в)
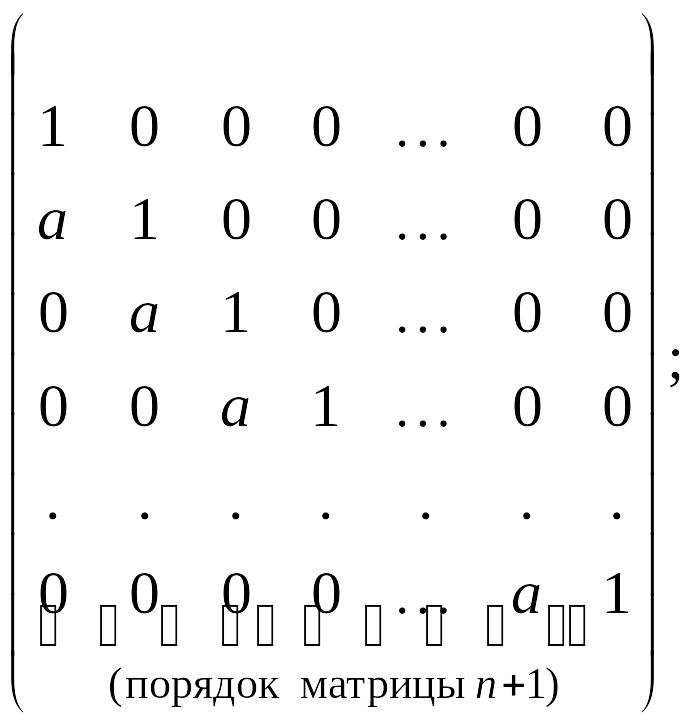г)
2.
Найти матрицу
из
уравнения
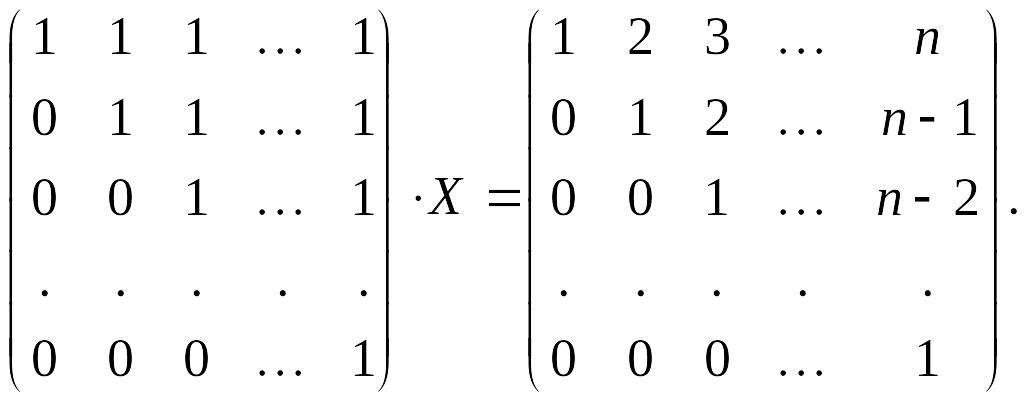
3.
Найти обратную
матрицу для матрицы
,
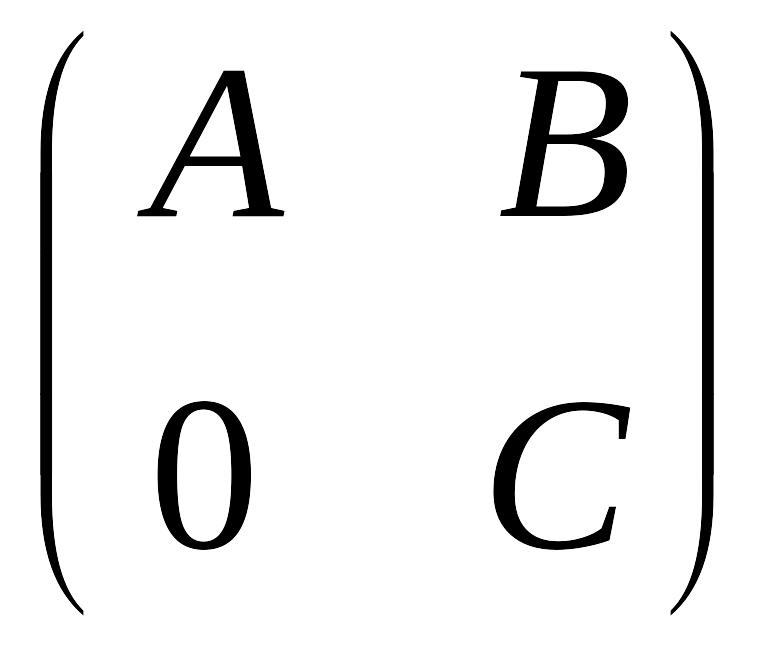где
–
обратимые матрицы одного порядка.
Используя полученный результат, вычислить
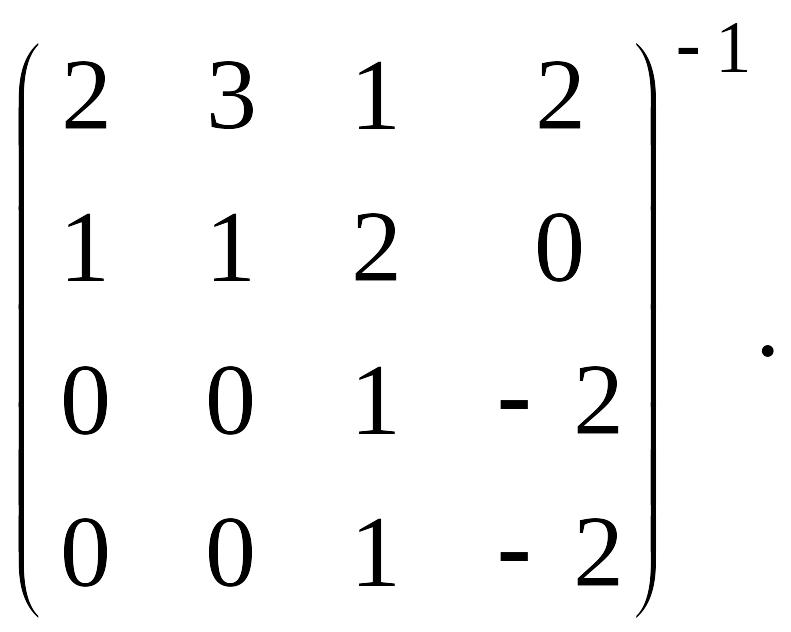
4.
Пусть
–
обратимые матрицы одного порядка.
Показать, что равенства
равносильны.
5.
Пусть
– матрицы
порядка
.
Доказать, что найдутся
чисел
,
не равные нулю одновременно, такие, что
матрица
необратима.
6. Пусть A – квадратная матрица порядка с нулями на главной диагонали и числами вне диагонали. Доказать, что при четных матрица А невырожденная, а при любом нечетном матрица А может быть и вырожденной и невырожденной. Привести соответствующие примеры.
7. Доказать, что если матрица А нильпотентная, то матрицы Е–А и Е+А обратимы.
8. Решить уравнение AX + X + A = 0, где А – заданная нильпотентная матрица.
9.
Указать, как изменится обратная матрица
если в
матрице А:
а) переставить i-ю и j–ю строки;
б) i-ю строку умножить на число с, не равное нулю;
в) к i-й строке прибавить j-ю, умноженную на число с.