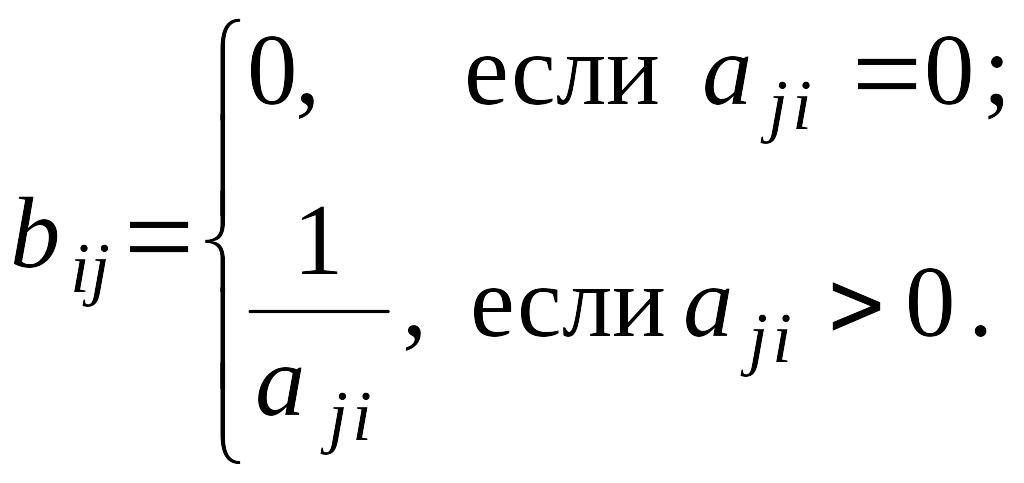1.3. Обратная матрица
Определение
1.
Квадратная
матрица
А называется обратимой
(невырожденной),
если существует матрица
такая,
что
.
В этом случае матрица называется обратной к матрице .
Обратная матрица может быть найдена несколькими способами: методом элементарных преобразований, методом присоединенной матрицы и посредством решения системы линейных уравнений.
Упражнение 1. Показать, что:
1) если
обратная матрица существует, то она
единственная и выполнено равенство
;
2) если
и
– квадратные матрицы и
,
то
.
Из второй части упражнения 1 следует, что в определении обратной матрицы достаточно проверить только одно из равенств АА-1=Е или А-1А=Е. Если одно из них будет выполнено (не выполнено), то второе будет выполнено (не выполнено) автоматически.
Теорема 1 (критерии обратимости). Для любой квадратной матрицы А следующие условия эквивалентны:
1) А – обратимая матрица;
2)
;
3) уравнение
имеет единственное решение
;
4) уравнение
имеет единственное решение для каждого
вектора
;
5) равенство
верно только для
.
Упражнение 2. Квадратная матрица такова, что в каждом ее столбце есть ровно два ненулевых элемента: диагональный, равный 1, и некоторый недиагональный, меньше 1. Показать, что матрица А обратима.
Решение.
Пусть
,
решение уравнения
.
Пусть индекс
такой, что
.
Обозначим
недиагональный ненулевой элемент
в
-й
строке матрицы
.
Тогда
и
.
Последнее равенство возможно только в
случае
.
В силу предположения
имеем
для всех
.
Таким образом, матрица
обратима (см.теорему 1, пункты 1 и 3).
Упражнение
3. Используя технику
решения предыдущей задачи, показать,
что матрица
,
элементы которой удовлетворяют условию
для всех
,
обратима (теорема Перрона).
Ниже рассмотрим условия обратимости и способы нахождения обратных матриц для матриц специального вида.
1. Обратимость блочных и блочно-диагональных матриц
Определение
2. Матрицы
,
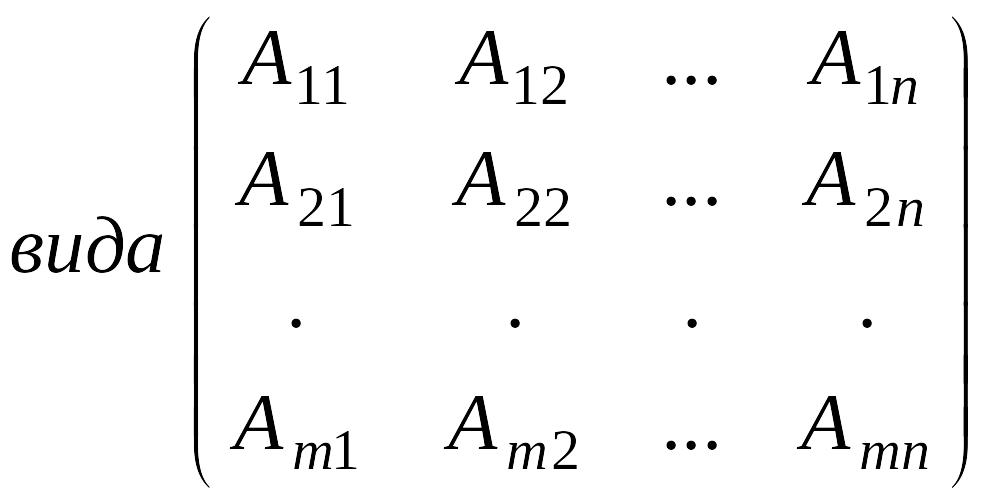элементы которых являются матрицами,
называются блочными.
Блочные матрицы, у которых
,
если
,
называются блочно-диагональными.
При
нахождении матриц, обратных
блочно-диагональным, часто поступают
таким образом, как если бы элементы
были числами.
Упражнение
4. Найти матрицу, обратную
квадратной матрице
,
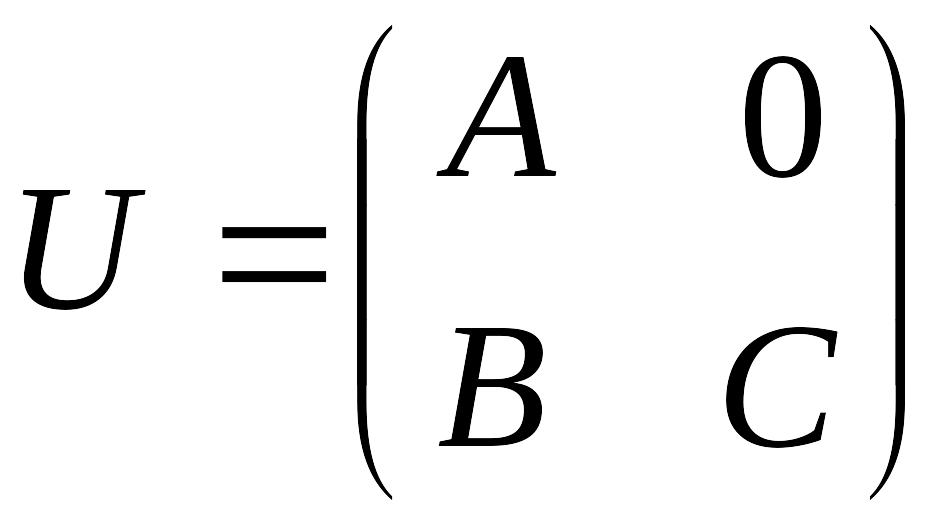где
– квадратные матрицы одной размерности
и
.
Решение.
Во-первых, заметим, что
существует, так как
(см. теорему Лапласа). Будем искать
в виде
,
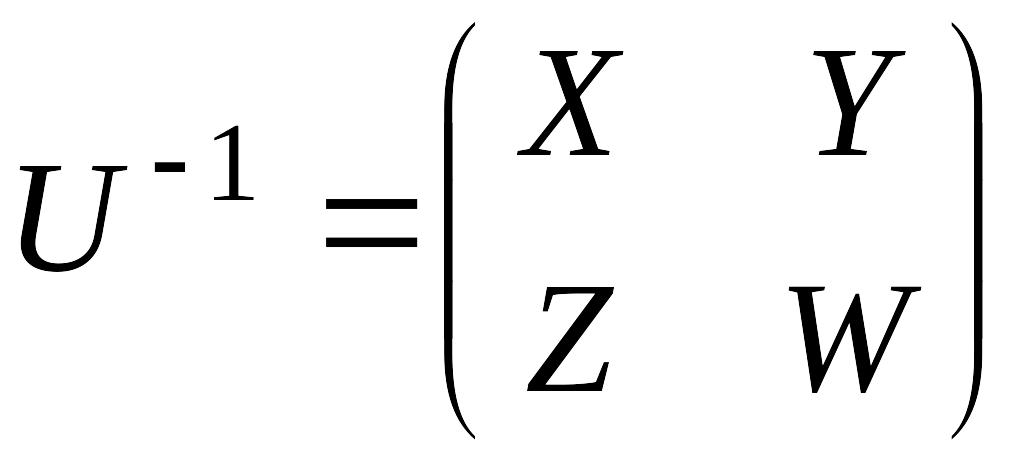где
– квадратные матрицы.
Найдем матрицы из системы
.
Из первого и третьего
уравнения
.
Из второго и четвертого
Таким
образом,
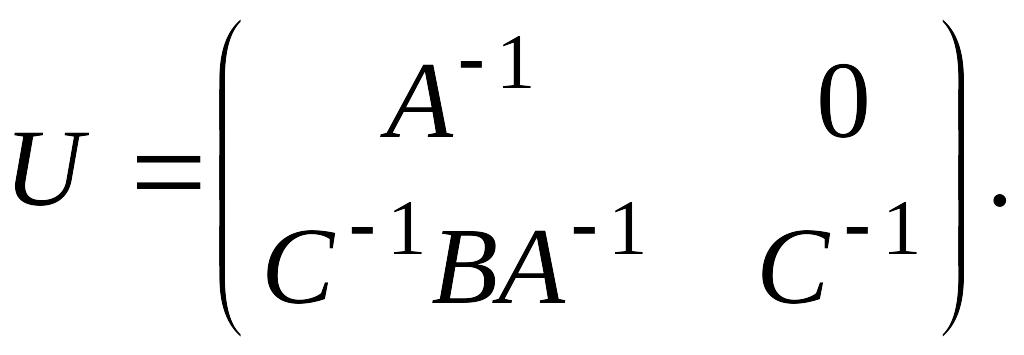
2. Обратимость матриц специального вида
В этом разделе мы опишем вид матриц, обратных матрицам, рассмотренным в п. 1.1.
Утверждение
1. Пусть
–
обратимая симметрическая матрица. Тогда
является симметрической.
Доказательство.
Обозначим
.
Покажем, что
.
Как известно,
,
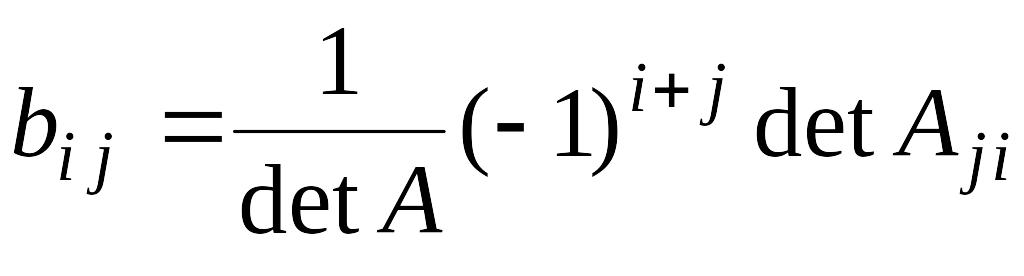где
получается из
вычеркиванием j-й
строки и i-го столбца.
Из равенства
следует, что
Таким образом,
Упражнение 5. Показать, что:
1) матрица, обратная унитарной (ортогональной), является унитарной (ортогональной);
2) матрица, обратная невырожденной эрмитовой, косоэрмитовой или кососимметрической, является эрмитовой, косоэрмитовой или кососимметрической соответственно.
Утверждение
2. Показать, что обратная матрица
для верхней (нижней) треугольной
невырожденной матрицы
является верхней (нижней) треугольной
матрицей.
Доказательство.
Докажем утверждение для верхней
треугольной матрицы непосредственно
по определению, указав попутно способ
отыскивания
.
Последовательно умножая столбцы второй матрицы на первую, получаем
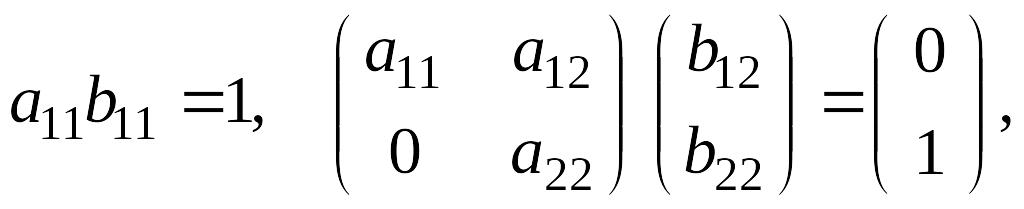
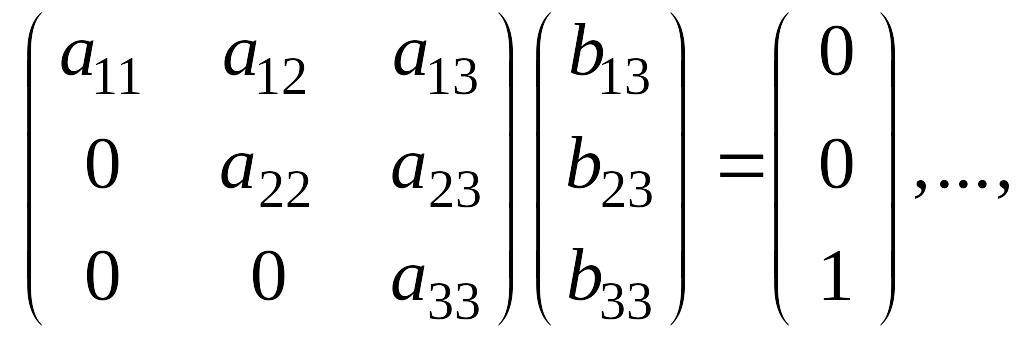
Так
как матрица
невырожденная, то все
.
Следовательно, определители матриц
всех рассмотренных систем отличны от
нуля и эти системы имеют единственные
решения. Запишем эти решения в столбцы
и дополним эти столбцы нулями, чтобы
получились столбцы размерности n.
Составим из этих столбцов матрицу
размерности
,
которая и будет обратной матрицей для
А.
Упражнение 6. Доказать предыдущее утверждение, используя метод элементарных преобразований и метод присоединенной матрицы.
Матрица
с целочисленными элементами называется
унимодулярной,
если ее определитель равен
.
Утверждение 3. Целочисленная матрица тогда и только тогда имеет целочисленную обратную матрицу, когда она является унимодулярной.
Доказательство.
Обозначим
Если − унимодулярная матрица, то из равенств
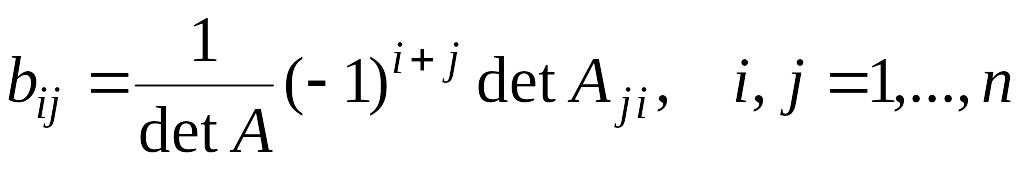
следует, что элементы являются целыми числами.
Пусть
теперь все элементы
– целые числа. Тогда из неравенства
получаем
Утверждение 4. Следующие два условия эквивалентны:
1)
матрицы
неотрицательны;
2) в каждом столбце и каждой строке матрицы ровно один элемент больше нуля, остальные элементы равны нулю.
Доказательство.
Пусть выполнено условие 1. Предположим,
что в k-м столбце
матрицы
есть два ненулевых элемента
,
.
Тогда для любого
произведение j-й строки
матрицы
на k-й столбец
матрицы
равно нулю (так как
),
то есть
.
Так
как
то
для всех
.
Значит, столбцы
матрицы
пропорциональны и матрица
необратима. Получили противоречие.
Аналогично доказывается утверждение
относительно строк матрицы А.
Если
выполнено условие 2, то
существует и ее элементы
определяются равенствами
