
- •Часть 1
- •1. Линейная алгебра
- •1.1. Основные классы квадратных матриц
- •Задачи для самостоятельного решения
- •1.2. Определители. Ранг матрицы
- •1.2.1. Вычисление определителей
- •1.2.2. Вычисление ранга матриц
- •Задачи для самостоятельного решения
- •1.3. Обратная матрица
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Как изменится матрица , если совершить аналогичные преобразования со столбцами матрицы а?
- •1.4. Жорданова нормальная форма
- •1.5. Возведение матриц в степень. Нильпотентные матрицы. След матрицы
- •Задачи для самостоятельного решения
- •1.6. Многочлены
- •Задачи для самостоятельного решения
- •2. Введение в анализ
- •2.1. Метод математической индукции
- •Алгоритм метода математической индукции
- •Решение. Используем метод математической индукции.
- •Задачи для самостоятельного решения
- •2.2. Пределы последовательностей
- •Упражнение 14. Найти
- •Примеры решения задач
- •Пример 2. Пусть , . Найти .
- •Задачи для самостоятельного решения
- •1. Вычислить пределы:
- •2.3. Предел функции. Непрерывность
- •Примеры решения задач
- •Пример 8. Доказать, что если функция непрерывна на отрезке и имеет обратную функцию, то она монотонна на этом отрезке.
- •Задачи для самостоятельного решения
- •3.1. Производная функции. Вычисление производной по определению
- •Если он существует и конечен, называется правосторонней (левосторонней) производной и обозначается . Если существует производная , то будем говорить, что дифференцируема в точке .
- •Теорема 2. Если существует производная , то функция непрерывна в точке .
- •Примеры решения задач Пример 1. Пусть Подобрать коэффициенты a и b так, чтобы функция была дифференцируемой в точке .
- •Заметим, что как произведение бесконечно малой функции на ограниченную , после замены получим
- •Задачи для самостоятельного решения
- •1. Показать, что функция , где – непрерывная функция и , не имеет производной в точке .
- •2. Пусть
- •3.2. Вычисление пределов функций с использованием методов дифференциального исчисления
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •1. Вычислить пределы
- •3.3. Выпуклые и вогнутые функции. Точки перегиба
- •Важную роль при исследовании функции на выпуклость вверх (выпуклость вниз) играют точки, в которых происходит изменение направления выпуклости функции.
- •В этом разделе будут рассмотрены основные свойства выпуклых вниз (вверх) функций, заданных на отрезке .
- •Задачи для самостоятельного решения
- •3.4. Основные теоремы дифференциального исчисления
- •Примеры решения задач
- •Обратим внимание на то, что является точкой перегиба функции . Оказывается, что этот факт верен для любой дважды дифференцируемой функции.
- •Так как , то , что и требовалось доказать.
- •Задачи для самостоятельного решения
- •6. Исследование функции нескольких переменных на экстремум
- •7. Доказательство тождеств с использованием свойств дифференцирования
- •Задачи для самостоятельного решения
- •3.6. Производные высших порядков
- •Задачи для самостоятельного решения
- •Заключение
- •Часть 1
- •394006 Воронеж, ул. 20-летия Октября, 84
1.2.2. Вычисление ранга матриц
Определение
1.
Максимальное число линейно независимых
столбцов (строк) матрицы
называется рангом
этой матрицы и обозначается
![]() .
.
Теорема 1. Наивысший порядок отличных от нуля миноров матрицы равен рангу этой матрицы.
Правило
вычисления ранга матрицы. При
вычислении ранга матрицы следует
переходить от миноров меньших порядков
к минорам больших порядков. Если уже
найден минор k-го
порядка
,
отличный от нуля, то требуют вычисления
лишь миноры (k+1)-го
порядка, окаймляющие минор
.
Если все они равны нулю, то ранг матрицы
равен
.
Говорят, что минор
![]() окаймляет
минор D,
если D
содержится внутри
,
другими словами, столбцы и строки,
образующие D,
входят в множество столбцов и строк,
образующих
.
окаймляет
минор D,
если D
содержится внутри
,
другими словами, столбцы и строки,
образующие D,
входят в множество столбцов и строк,
образующих
.
Определение 2. Под элементарным преобразованием строк (столбцов) матрицы А понимаются:
а) перестановка местами двух строк (столбцов);
б) умножение строки (столбца) на любое число, неравное нулю;
в) сложение любой строки (столбца) с другой строкой (столбцом), умноженной на некоторое число.
Теорема 2. Элементарные преобразования строк (столбцов) матрицы не меняют ранга этой матрицы.
Упражнение 1. Пусть
 .
.
Показать, что

Упражнение
2.
Пусть
![]() матрица
размерности
матрица
размерности
![]() ,
имеющая
ранг 1. Доказать, что найдутся
матрицы
,
имеющая
ранг 1. Доказать, что найдутся
матрицы
![]() размерностей
размерностей
![]() и
и
![]() соответственно такие, что
соответственно такие, что
![]() .
.
Решение. Так как ранг матрицы равен 1, то все ее строки пропорциональны одной (скажем, первой). Тогда
 .
.
Осталось
положить
![]() .
.
Упражнение
3.
Пусть
квадратная матрица А
порядка
![]() и
и
![]() .
Найти ранг присоединенной матрицы
.
Найти ранг присоединенной матрицы
![]() где
где
![]() алгебраическое
дополнение элемента
алгебраическое
дополнение элемента
![]() матрицы
.
матрицы
.
Решение.
1) если
![]() ,
то
,
то
![]() .
Значит,
.
Значит,
![]() ;
;
2)
если
![]() то все
миноры (n–1)-го
порядка равны 0. Следовательно,
то все
миноры (n–1)-го
порядка равны 0. Следовательно,
![]() нулевая
матрица и ее ранг равен нулю;
нулевая
матрица и ее ранг равен нулю;
3)
если
![]() то
запишем
в виде
то
запишем
в виде
![]()
![]() –
в виде
–
в виде
![]() ,
где
,
где
![]() вектор-столбцы,
состоящие из n
элементов. Обозначим множество
(пространство) всевозможных линейных
комбинаций векторов
вектор-столбцы,
состоящие из n
элементов. Обозначим множество
(пространство) всевозможных линейных
комбинаций векторов
![]()
![]() символом
символом
![]() .
Под размерностью пространства
понимается количество векторов,
образующих базис этого пространства,
и обозначается
.
Под размерностью пространства
понимается количество векторов,
образующих базис этого пространства,
и обозначается
![]() .
Так как
.
Так как
![]() ,
то
,
то
![]() .
Так как
.
Так как
![]() ,
только если
,
только если
![]() для всех
для всех
![]() ,
то
,
то
![]() .
Это означает, что выполнено равенство
.
Это означает, что выполнено равенство![]() .
.
Задачи для самостоятельного решения
Вычислить определители приведением к треугольному виду:
а)
 ,
б)
,
б)
 ,
,
в)
 ,
г)
,
г)


2. Вычислить определители методом рекуррентных соотношений:
а)
 ,
б)
,
б)
 ,
,
в) ,
г)
,
г)
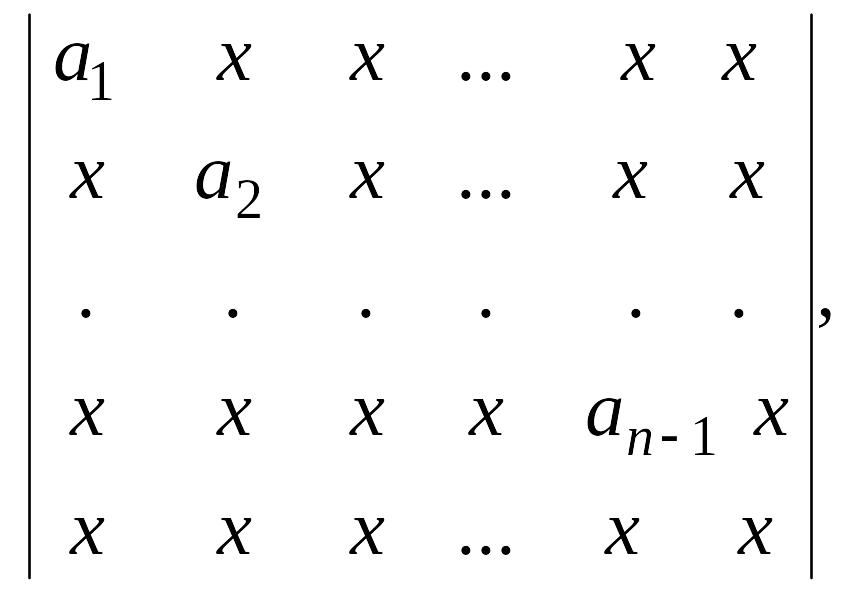
д)
 е)
е)

3. Рядом Фибоначчи называется числовой ряд, который начинается числами 1, 2 и в котором каждое следующее число равно сумме двух предыдущих, то есть, 1, 2, 3, 5, 8, 13, 21, … .
Доказать, что -й член ряда Фибоначчи равен следующему определителю -го порядка:
 .
.
4. Вычислить определители методом разложения на линейные множители:
а)
 ,
б)
,
б)
 ,
,
в)
 ,
г)
,
г)

5. Используя теорему Лапласа, вычислить определители:
а)
 ,
б)
,
б)
 ,
в)
,
в)
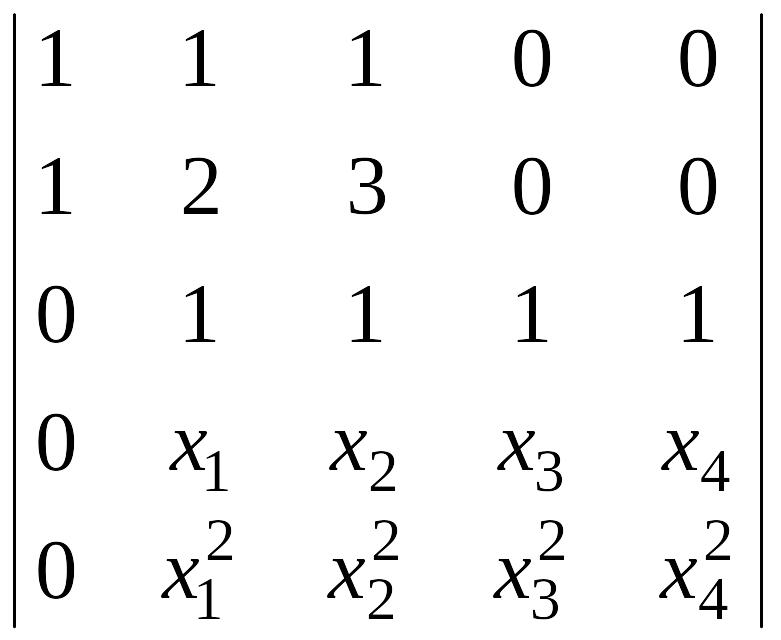 .
.
6. Вычислить определители, представляя их в виде произведения определителей:
а)
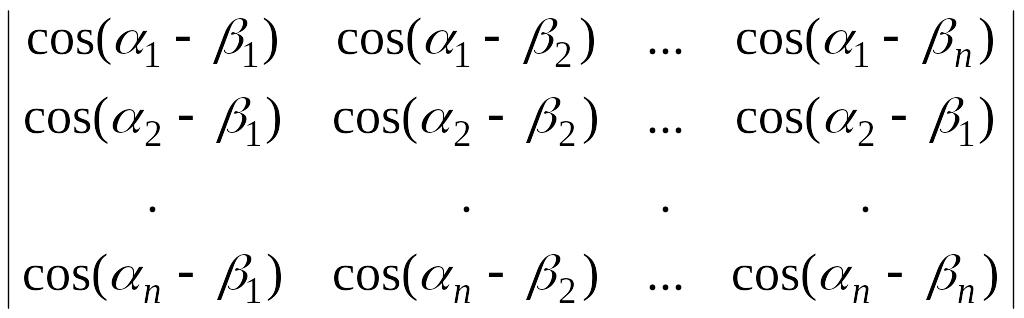 ,
,
б)
 ,
,
в)
 .
.
7.
Показать,
что если
![]() ,
то
,
то
 .
.
8.
Доказать,
что определитель матрицы
 ,
где
– произвольная
квадратная матрица, равен нулю.
,
где
– произвольная
квадратная матрица, равен нулю.
9.
Доказать,
что из
![]() следует равенство
следует равенство
 ,
где
,
где
![]() – квадратные
матрицы одного порядка.
– квадратные
матрицы одного порядка.
10.
Вычислить
определитель
![]() посредством умножения его на определитель
посредством умножения его на определитель
![]() .
.
а)
 ,
,
 ;
;
б)
 ,
,
 .
.
11.
Пусть
![]() –
квадратные матрицы одного порядка.
Доказать, что
–
квадратные матрицы одного порядка.
Доказать, что
 .
.
12. Доказать, что ранг произведения двух матриц не превосходит ранга каждой из матриц-сомножителей.
13. Доказать, что приписывание к матрице одной строки (одного столбца) либо не изменяет ранга этой матрицы, либо увеличивает его на единицу.
14. Доказать, что любую матрицу ранга можно представить в виде суммы матриц ранга единица.
Указание. Элементарными преобразованиями привести исходную матрицу к матрице, содержащей ровно ненулевых элементов, и представить последнюю в виде суммы матриц, каждая из которых имеет единственный нулевой элемент.
