
- •Часть 1
- •1. Линейная алгебра
- •1.1. Основные классы квадратных матриц
- •Задачи для самостоятельного решения
- •1.2. Определители. Ранг матрицы
- •1.2.1. Вычисление определителей
- •1.2.2. Вычисление ранга матриц
- •Задачи для самостоятельного решения
- •1.3. Обратная матрица
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Как изменится матрица , если совершить аналогичные преобразования со столбцами матрицы а?
- •1.4. Жорданова нормальная форма
- •1.5. Возведение матриц в степень. Нильпотентные матрицы. След матрицы
- •Задачи для самостоятельного решения
- •1.6. Многочлены
- •Задачи для самостоятельного решения
- •2. Введение в анализ
- •2.1. Метод математической индукции
- •Алгоритм метода математической индукции
- •Решение. Используем метод математической индукции.
- •Задачи для самостоятельного решения
- •2.2. Пределы последовательностей
- •Упражнение 14. Найти
- •Примеры решения задач
- •Пример 2. Пусть , . Найти .
- •Задачи для самостоятельного решения
- •1. Вычислить пределы:
- •2.3. Предел функции. Непрерывность
- •Примеры решения задач
- •Пример 8. Доказать, что если функция непрерывна на отрезке и имеет обратную функцию, то она монотонна на этом отрезке.
- •Задачи для самостоятельного решения
- •3.1. Производная функции. Вычисление производной по определению
- •Если он существует и конечен, называется правосторонней (левосторонней) производной и обозначается . Если существует производная , то будем говорить, что дифференцируема в точке .
- •Теорема 2. Если существует производная , то функция непрерывна в точке .
- •Примеры решения задач Пример 1. Пусть Подобрать коэффициенты a и b так, чтобы функция была дифференцируемой в точке .
- •Заметим, что как произведение бесконечно малой функции на ограниченную , после замены получим
- •Задачи для самостоятельного решения
- •1. Показать, что функция , где – непрерывная функция и , не имеет производной в точке .
- •2. Пусть
- •3.2. Вычисление пределов функций с использованием методов дифференциального исчисления
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •1. Вычислить пределы
- •3.3. Выпуклые и вогнутые функции. Точки перегиба
- •Важную роль при исследовании функции на выпуклость вверх (выпуклость вниз) играют точки, в которых происходит изменение направления выпуклости функции.
- •В этом разделе будут рассмотрены основные свойства выпуклых вниз (вверх) функций, заданных на отрезке .
- •Задачи для самостоятельного решения
- •3.4. Основные теоремы дифференциального исчисления
- •Примеры решения задач
- •Обратим внимание на то, что является точкой перегиба функции . Оказывается, что этот факт верен для любой дважды дифференцируемой функции.
- •Так как , то , что и требовалось доказать.
- •Задачи для самостоятельного решения
- •6. Исследование функции нескольких переменных на экстремум
- •7. Доказательство тождеств с использованием свойств дифференцирования
- •Задачи для самостоятельного решения
- •3.6. Производные высших порядков
- •Задачи для самостоятельного решения
- •Заключение
- •Часть 1
- •394006 Воронеж, ул. 20-летия Октября, 84
Задачи для самостоятельного решения
1.
а)
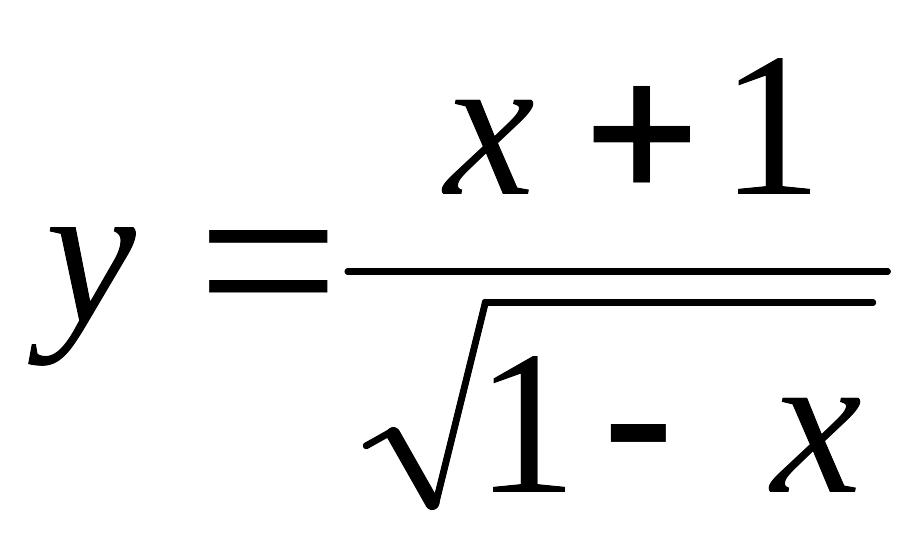 ,
найти
,
найти
![]() ,
б)
,
б)
![]() ,
найти
,
найти
![]() .
.
2.
Показать,
что
![]() ,
где
,
где
![]() ,
,
![]() ,
,
![]() .
.
3.
Доказать,
что
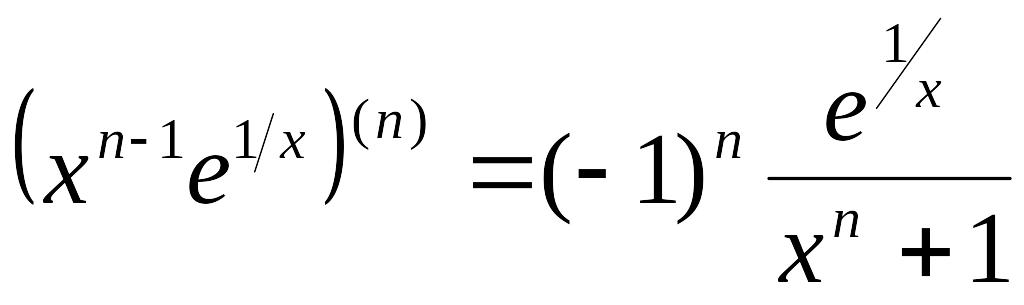 .
.
4.
Найти
производную
второго порядка от функции, заданной
неявно:
![]() ,
,
![]() .
.
5. Вывести формулу для второй производной функции, обратной к заданной функции .
Заключение
Задачи, предлагаемые в пособии, носят нестандартный характер и требуют от студента не только прочных знаний, но и творческого подхода. Большинство задач иллюстрируют в упрощенной форме ту или иную глубокую математическую идею.
Данное пособие будет полезно широкому кругу читателей, интересующихся строгими математическими доказательствами и неожиданными идеями, и в первую очередь студентам различных вузов, аспирантам, преподавателям, всем интересующимся математикой.
Пособие может быть использовано как преподавателями для работы в математических кружках, так и студентами для подготовки к олимпиадам.
ОТВЕТЫ И УКАЗАНИЯ
1. Линейная алгебра
1.2. Определители. Ранг матрицы
1.
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() .
.
2.
а)![]() ;
б)
;
б)
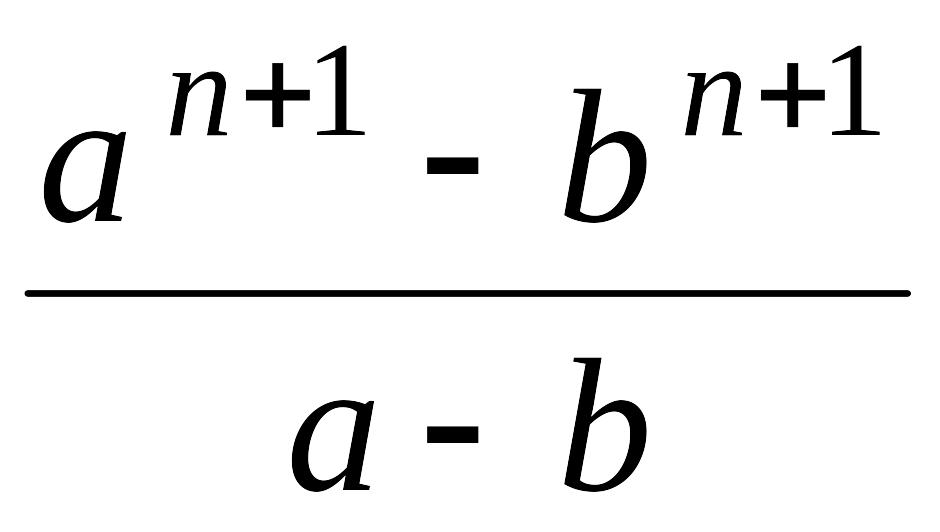 ;
в)
;
в)
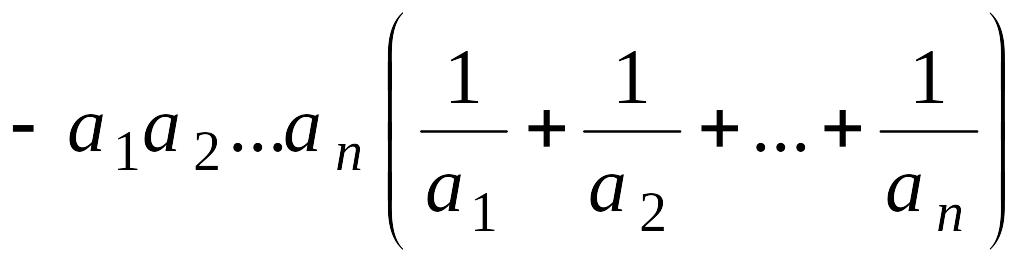 ,
,
е)
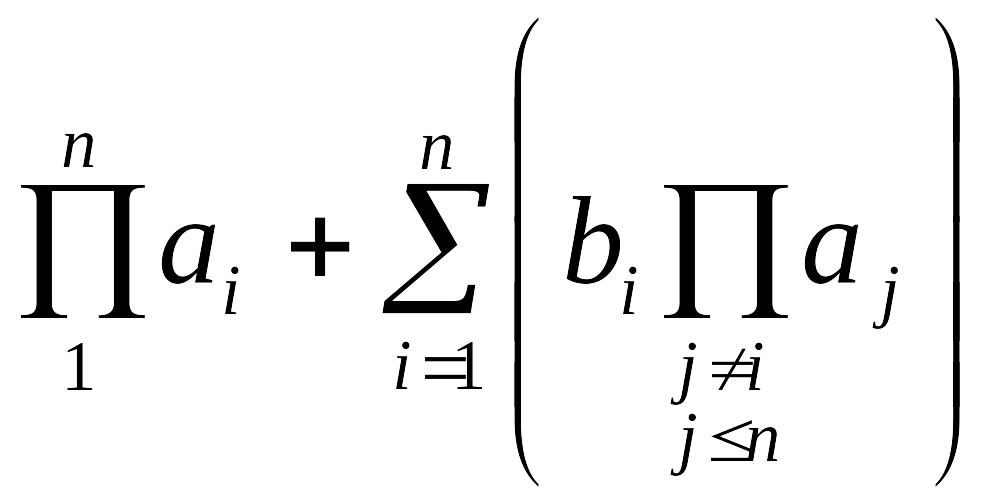
4.
а)
![]() ;
б)
;
б)
![]() ;в)
;в)
![]() .
.
5.
а)
![]() ;
б)
;
б)![]() ;
;
в)
![]() .
.
6.
а) 0, если n
> 2;
![]() ,
если
;
,
если
;
б)
![]() ;
в)
0, если n
> 2;
;
в)
0, если n
> 2;
![]() ,
если
.
,
если
.
10.
а) 24; б)
![]() .
.
1.3. Обратная матрица
1.а)
 ;
;
б)
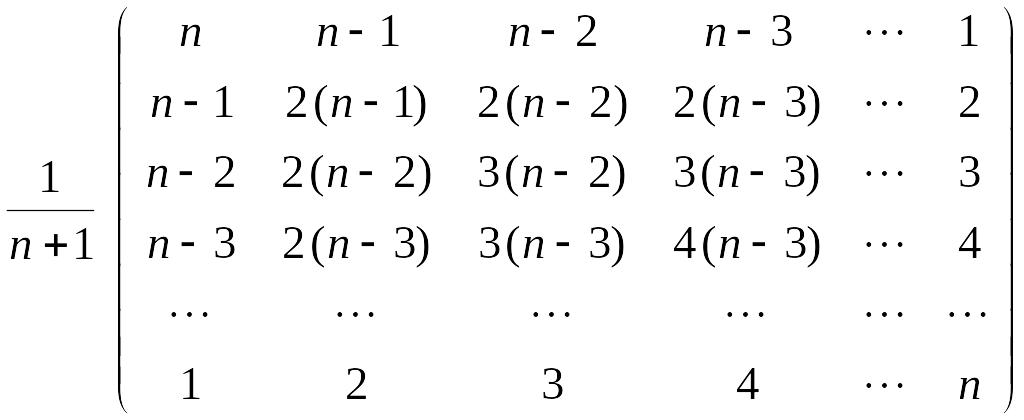 ;
;
в)
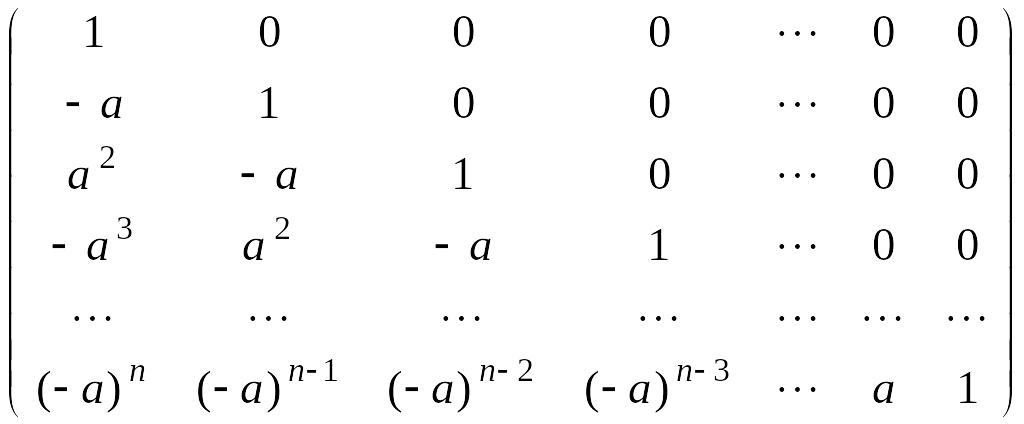 ;
;
г)
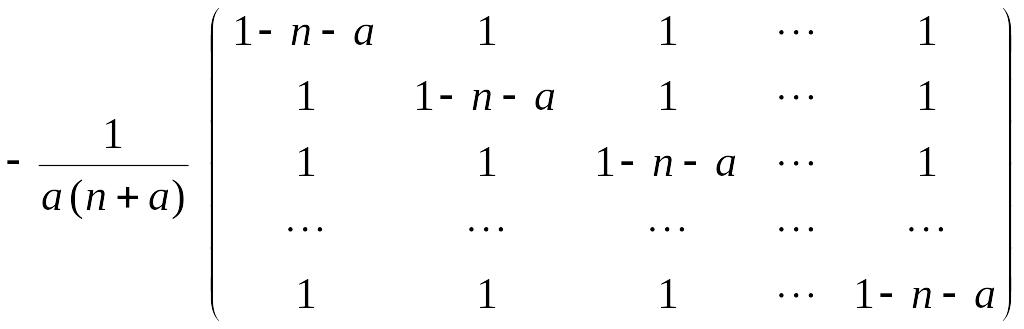 .
.
2.
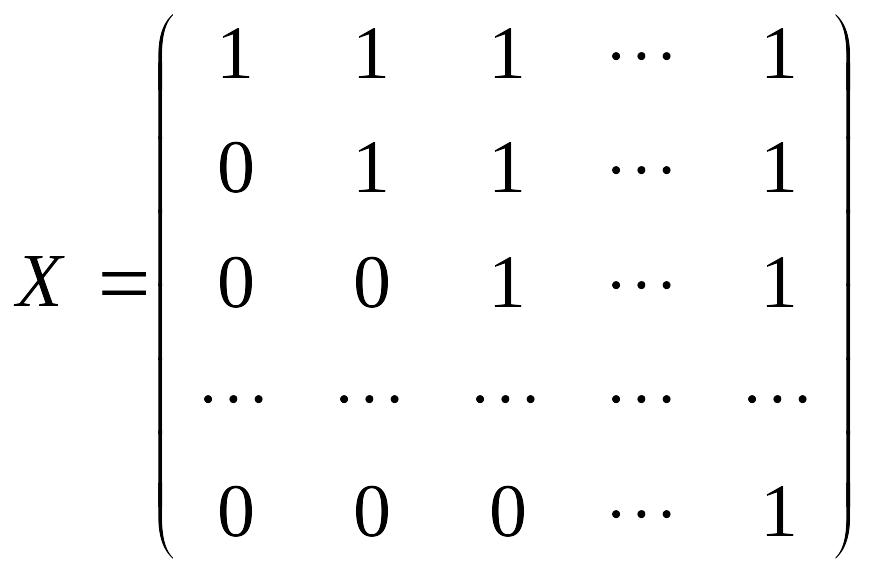 .
.
3.
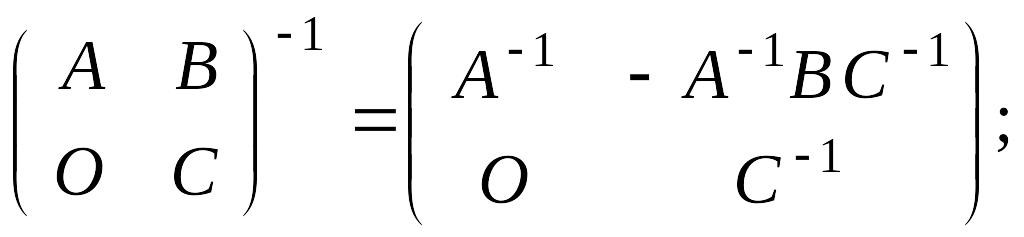
 .
.
4. Указание. Доказать, что каждое последующее равенство следует из предыдущего и первое следует из последнего.
5.
Указание.
Показать, что
![]() можно выбрать таким образом, что матрица
можно выбрать таким образом, что матрица
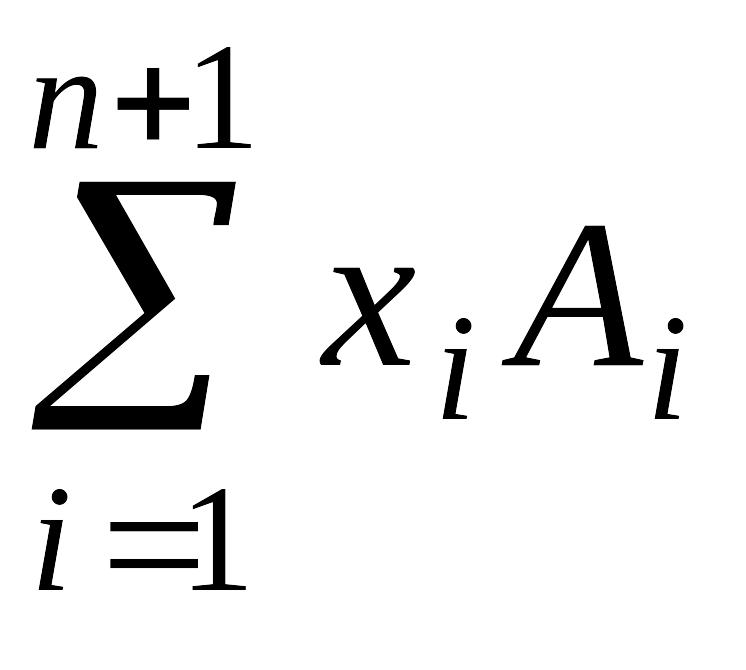 содержит один нулевой столбец.
содержит один нулевой столбец.
6.
 .
.
7.
Указание.
Сравнить с формулами
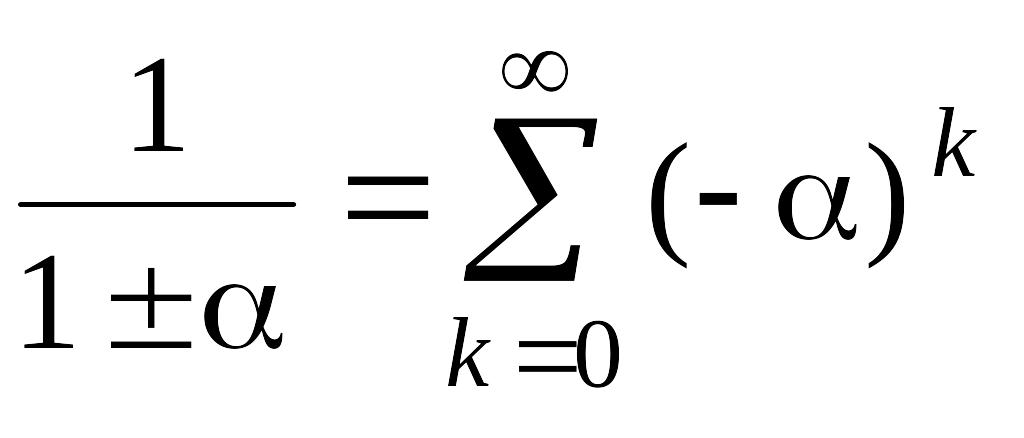 .
.
![]() ;
;
![]() ,
если
,
если
![]() .
.
8. Указание. Использовать результаты задачи 7.
9.
а) поменяются
местами i
– й и j-й
столбцы; б)
i
– й столбец
умножится на 1/с;
в)
из j-
го столбца вычтется i
– й, умноженный
на с.
Аналогичным образом преобразуются
строки матрицы
![]() .
.
10. Указание. Использовать результат задачи 7.
1.5. Возведение матриц в степень. Нильпотентные матрицы.
След матрицы.
а)
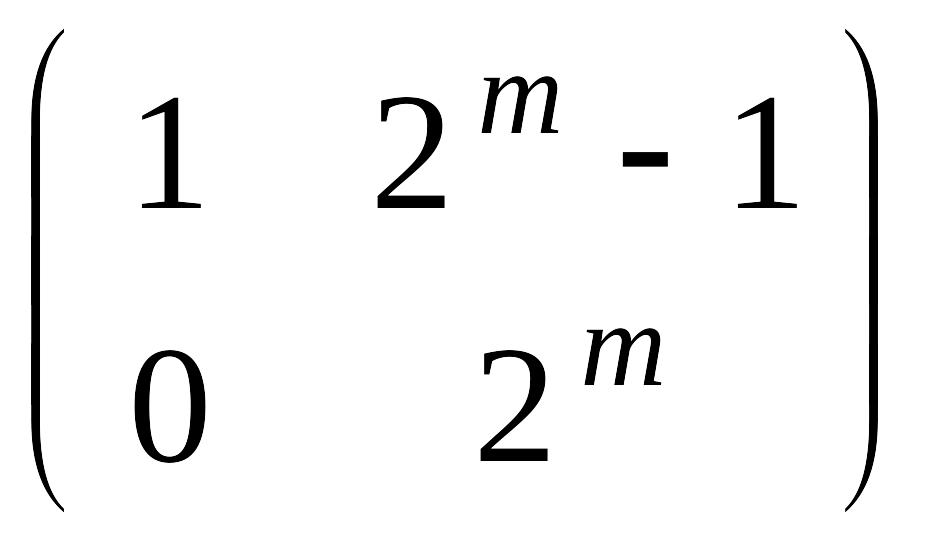 ;
б)
;
б)
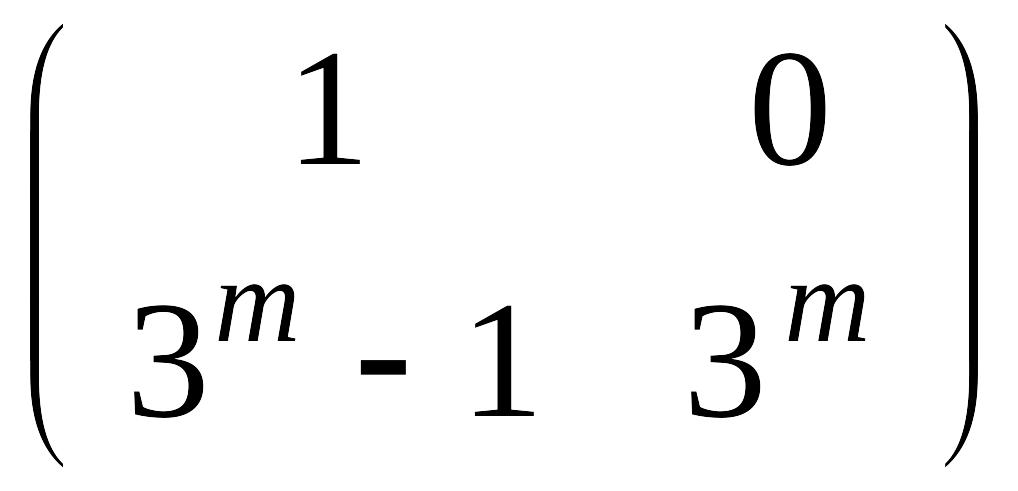 ;
в)
;
в)
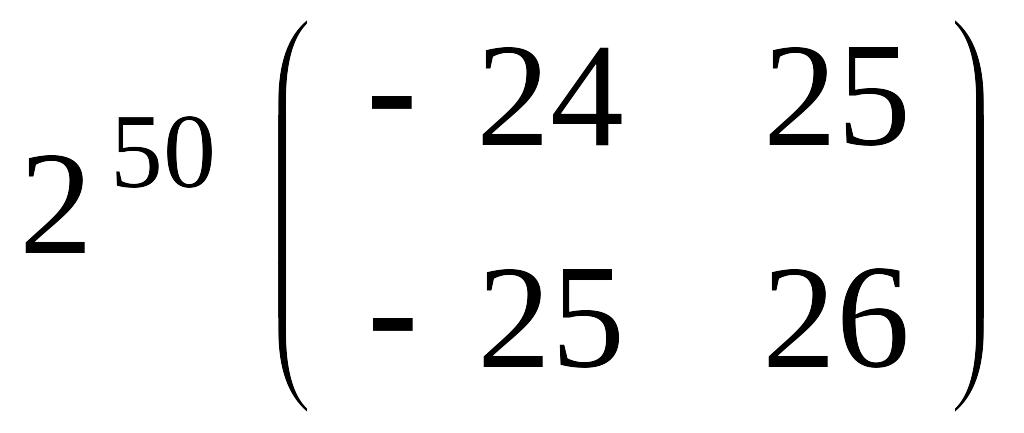 ;
г)
;
г)
 .
.
2.
а)
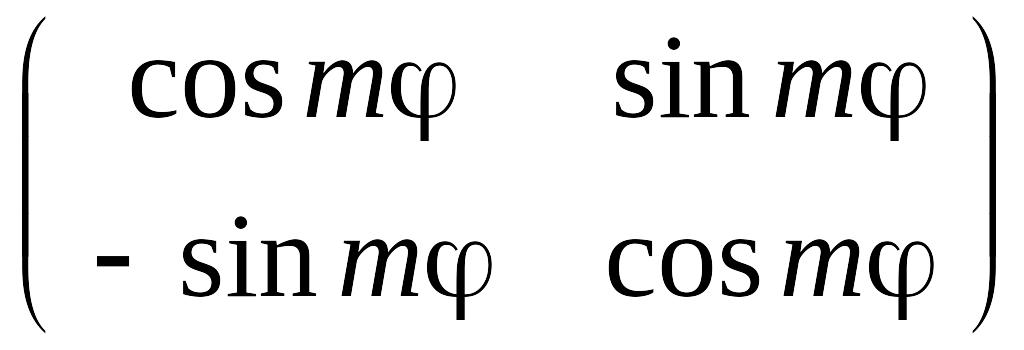 ,
б)
,
б)
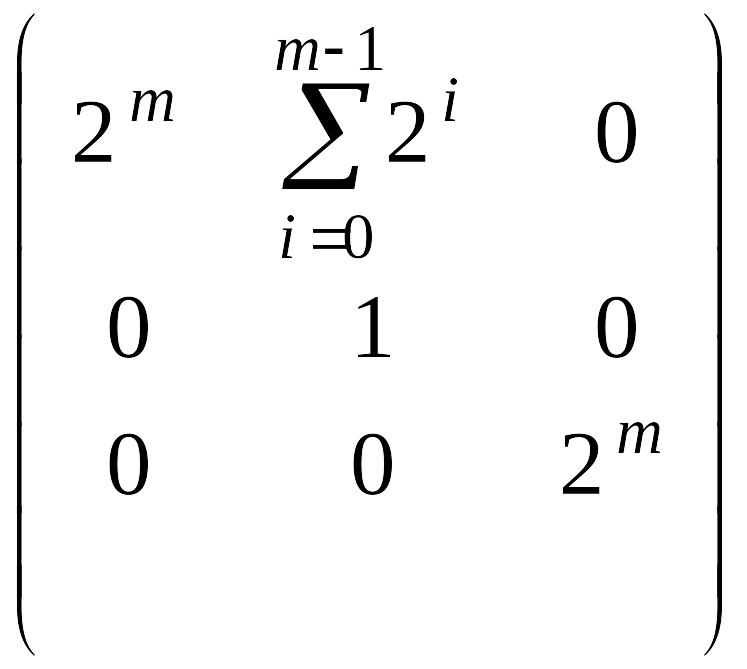 .
4.
.
4.![]() и
и
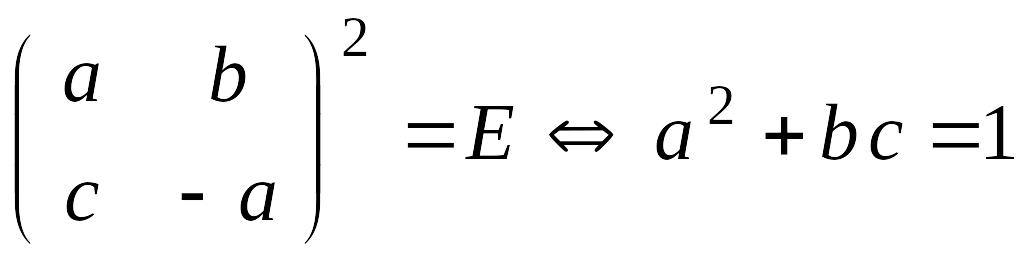 ;
;
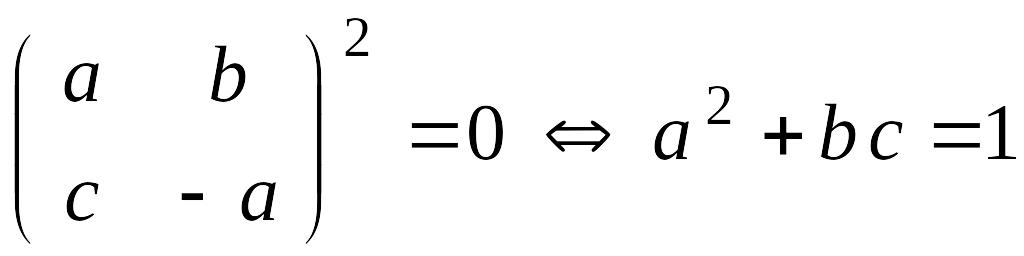 .
7.
.
7.
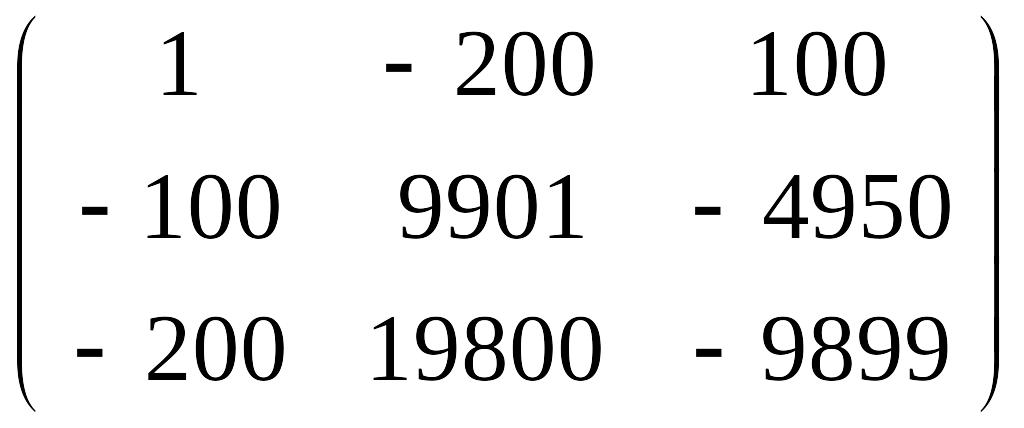 .
8.
Указание.
Вычислить
.
8.
Указание.
Вычислить
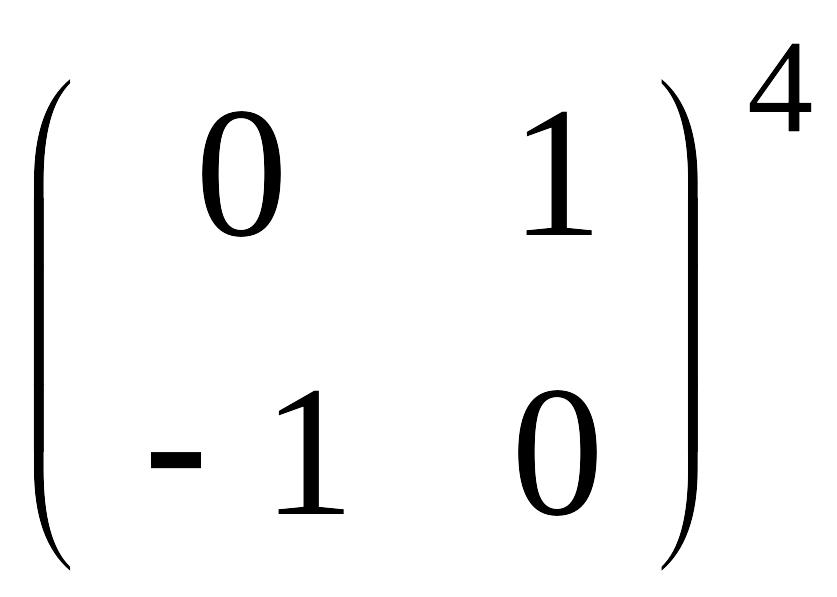 .
.
 .
9.
Указание. Вычислить
.
9.
Указание. Вычислить
![]() .
10.
.
10.
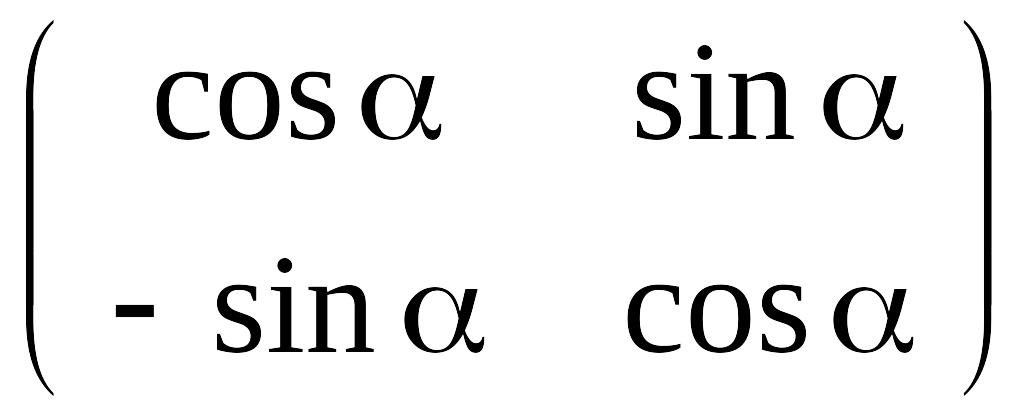 .
11.
Указание.
Воспользоваться формулой бинома Ньютона.
12.
.
11.
Указание.
Воспользоваться формулой бинома Ньютона.
12.
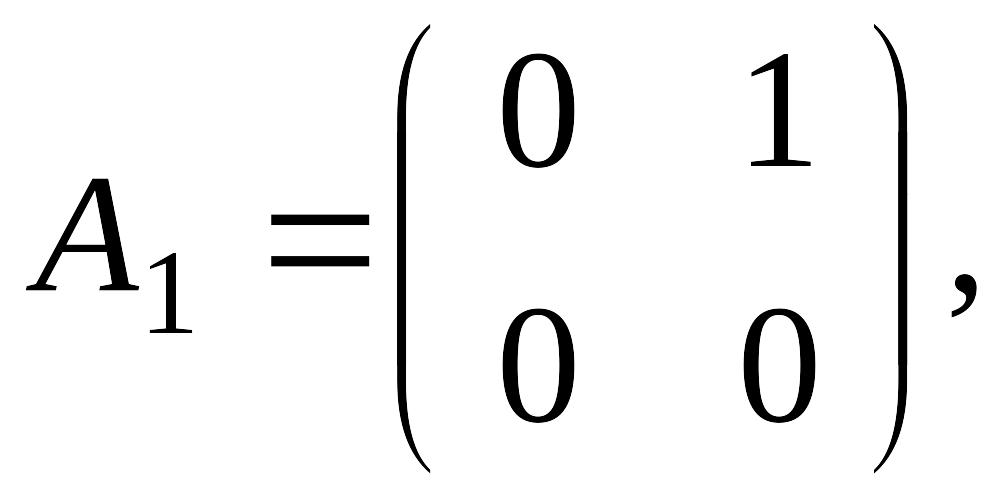
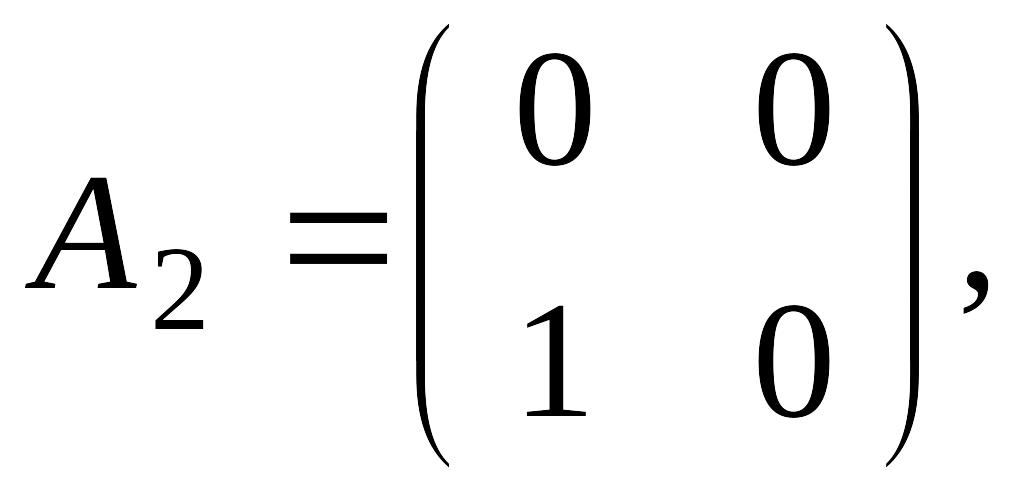
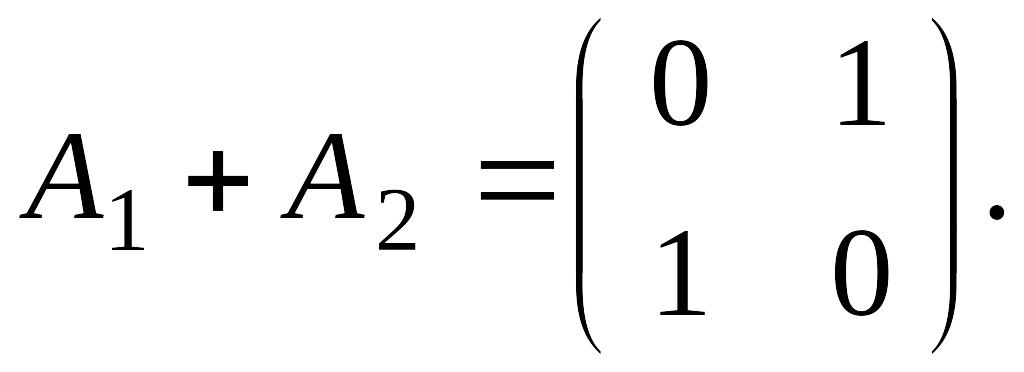
15.
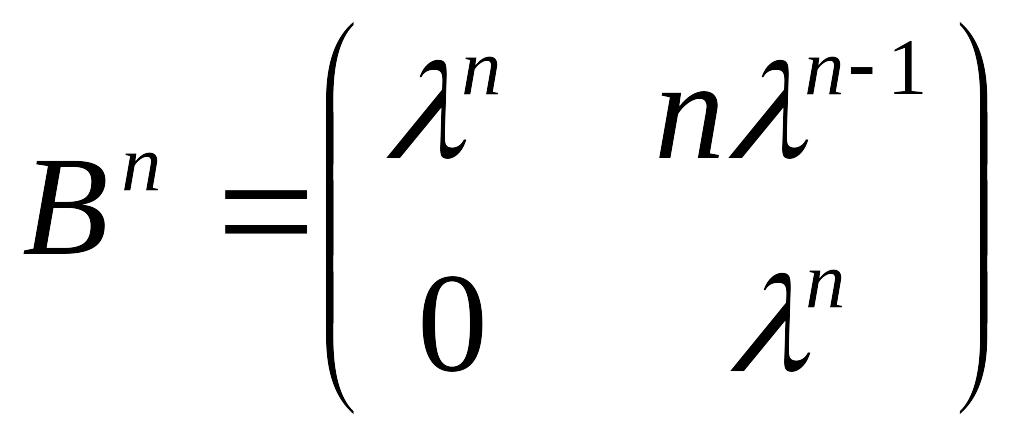 .
.
2. Введение в анализ
2.2. Пределы последовательностей
1.
а) 0; б)
0; в)
![]() ;
г)
1; д)
;
г)
1; д)
![]() ;
е)
3; ж)
;
е)
3; ж)
![]() ;
з)
2.
;
з)
2.
3.
а)
0; б)
![]() ;
в)
;
г)
.
;
в)
;
г)
.
4.
а)
1; б)
![]() ;
в)
0; г)
0; д)
;
в)
0; г)
0; д)
![]() .
.
5.
Равен 1, если
![]() ;
принадлежит [-1; 1] или не существует,
если а
= 0.
;
принадлежит [-1; 1] или не существует,
если а
= 0.
6.
Указание: использовать неравенство
![]() .
.
7.
![]() ;
;
![]() .
.
8.
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
… .
,
… .
2.3. Предел функции. Непрерывность
1.
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]() .
.
2.
![]()
![]()
5. а) 0; б) 0,5.
7.
![]() ,
если x
– рационально;
,
если x
– рационально;
![]() ,
если x
– иррационально.
,
если x
– иррационально.
3. Дифференциальное исчисление
3.1. Производная функции. Вычисление производной по определению
2.
![]() ;
;
![]() .
.
3.2. Вычисление пределов функций с использованием методов
дифференциального исчисления
1.
б)
![]() ;
в)
0; г)
;
в)
0; г)
![]() ;
д)
;
д)
![]() ;
е)
0; ж)
6; з)
8.
;
е)
0; ж)
6; з)
8.
2.
б)
![]() ;
;![]() .
4. а)
.
4. а)
![]() ;
б)
.
;
б)
.
3.3. Выпуклые и вогнутые функции. Точки перегиба
6.
а) при
![]() − выпуклость вверх, при
− выпуклость вверх, при
![]() – выпуклость вниз,
– выпуклость вниз,
![]() − точки перегиба,
− точки перегиба,
![]() ;
б)
при
;
б)
при
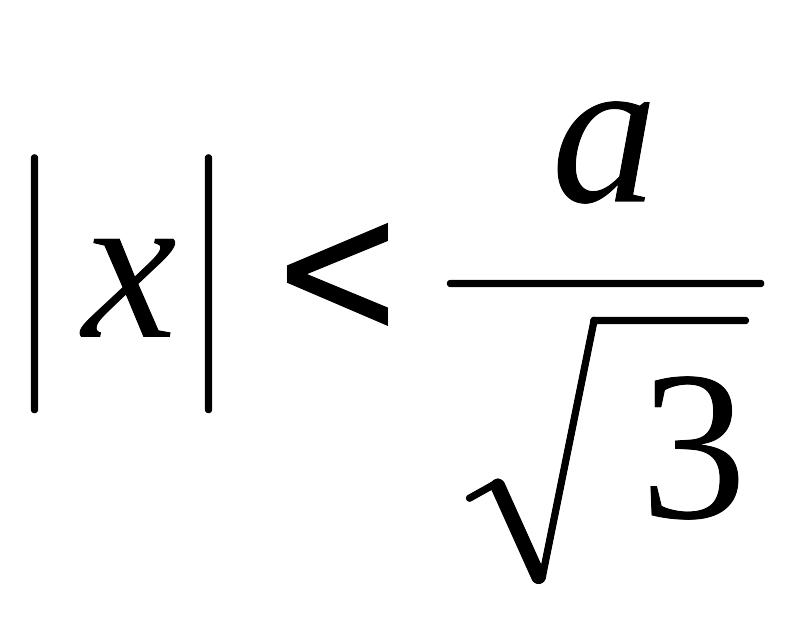 − выпуклость вверх, при
− выпуклость вверх, при
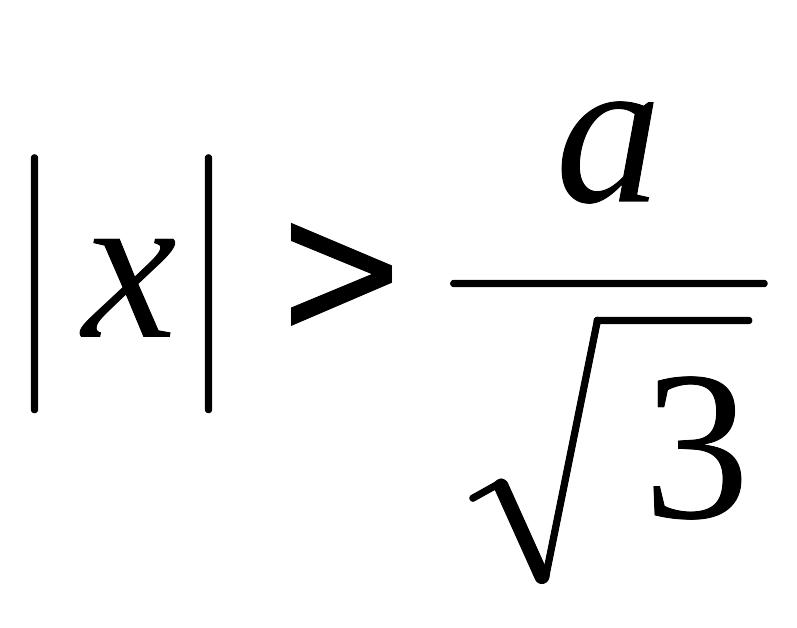 − выпуклость вниз,
− выпуклость вниз,
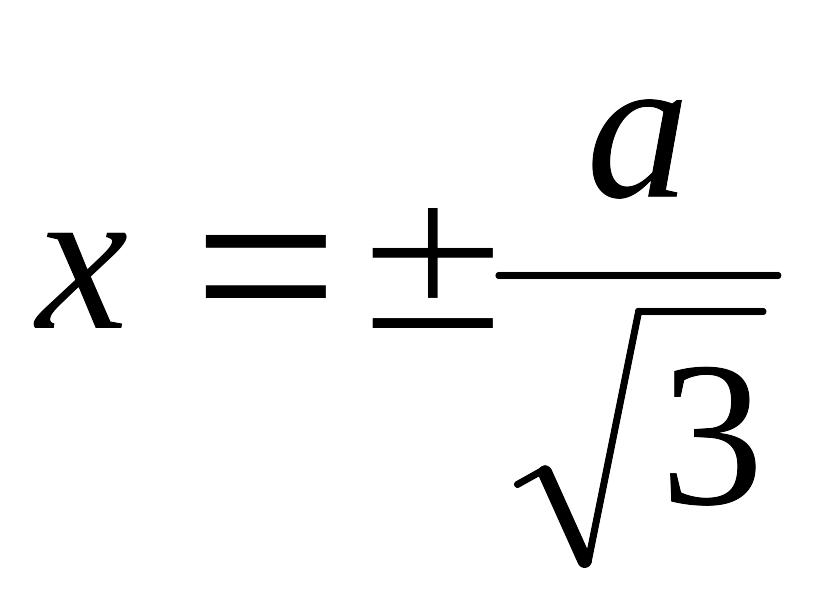 − точки перегиба;
− точки перегиба;
в)
при
![]() − выпуклость вниз, при
− выпуклость вниз, при
![]() −
выпуклость вверх,
−
выпуклость вверх,
![]() − точки перегиба,
.
7.
− точки перегиба,
.
7.
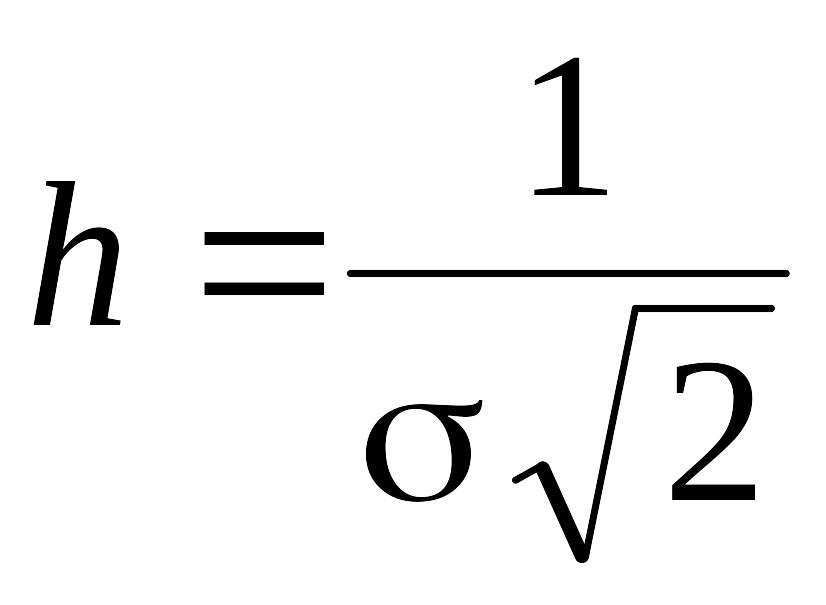 .
.
3.4. Основные теоремы дифференциального исчисления
1.
![]() .
.
2.
![]() .
.
10.
а) один
корень; б)
два корня; в)
два корня, если
![]() ,
корней нет, если
,
корней нет, если
![]() ,
где
- положительный корень уравнения
,
где
- положительный корень уравнения
![]() .
.
3.6. Производные высших порядков
1.
а)
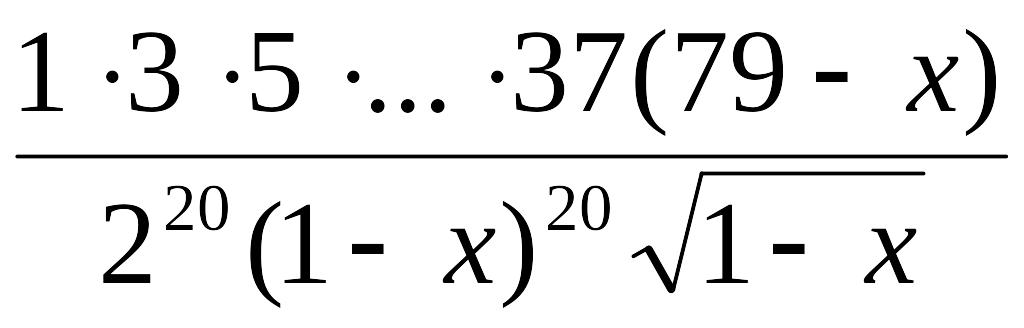 .
.
Указание.
Воспользоваться
равенством
![]() ;
;
б)
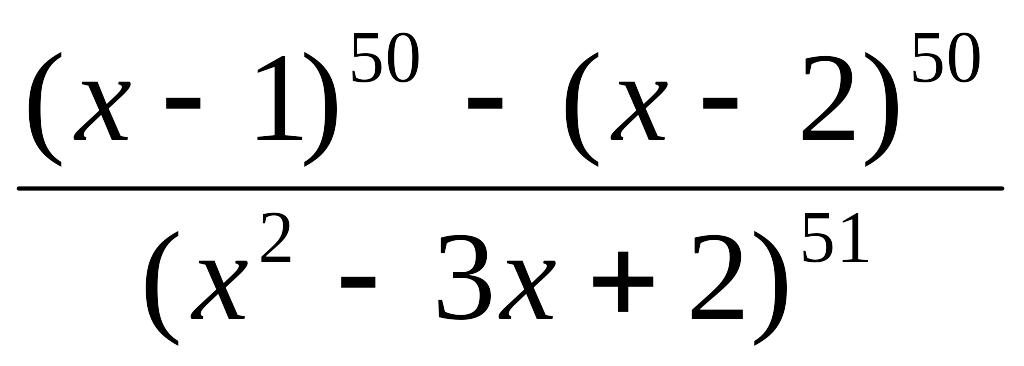 .
.
4.
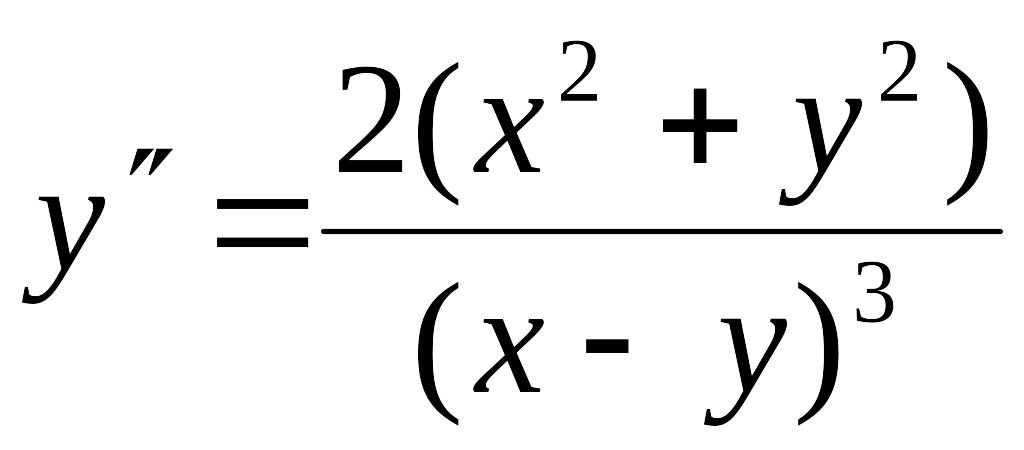 .
.
5.
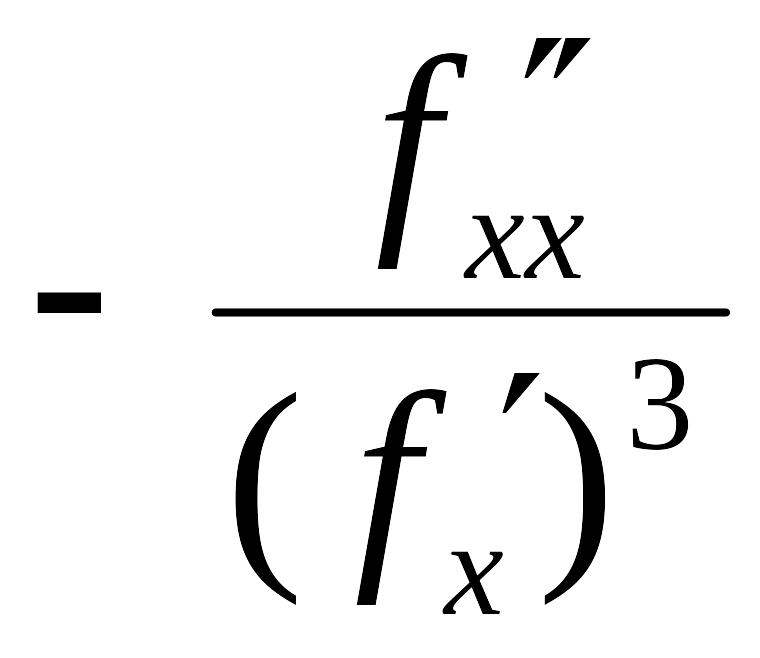
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. Лефор, Г. Алгебра и анализ./ Г. Лефор − М.: Изд-во Наука. 1975. − 462 с.
2.Виноградова, И.А. Задачи и упражнения по математическому анализу.
/ И.А. Виноградова, С.Н. Олехник, В.А. Садовничий − М.: Изд-во МГУ 1988. − 300 с.
3. Фихтенгольц, Г.М. Курс дифференциального и интегрального исчисления: учебник / Г.М. Фихтенгольц. − М.: Физматлит, 2003. Т.1. − 80 с.
4. Кудрявцев, Л.Д. Краткий курс математического анализа: учебник / Л.Д. Кудрявцев. −М.: Физматлит, 2003. Т. 1. − 400 с.
5. Никольский, С.М. Курс математического анализа: учебник / С.М. Никольский. − М.: Наука, 1990. − Т.1. − 528 с.
6. Демидович, Б.П. Сборник задач и упражнений по математическому анализу /
Б.П.Демидович − М.: Наука, 2001. − 545 с.
О Г Л А В Л Е Н И Е
ВВЕДЕНИЕ………………………………………………………………………..3
1. ЛИНЕЙНАЯАЛГЕБРА………………………………………………............... 1.1. Основные классы квадратных матриц………………………….............. 1.2. Определители. Ранг матрицы…………………………………………… 1.2.1. Вычисление определителей………………………………………. 1.2.2. Вычисление ранга матриц………………………………………… 1.3. Обратная матрица……………………………………………………….. 1.4. Жорданова нормальная форма...………………………………………… 1.5. Возведение матриц в степень. Нильпотентные матрицы. …………… След матрицы…………………………………………………………….. 1.6. Многочлены……………………………………………………………… 2. ВВЕДЕНИЕ В АНАЛИЗ……………………………………………………… 2.1. Метод математической индукции………………………………………. 2.2. Пределы последовательностей………………………………………….. 2.3. Предел функции. Непрерывность……………………………….............. 3. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ…………………………............... 3.1. Производная функции. Вычисление производной по определению…………………………………………………………… 3.2. Вычисление пределов функций с использованием методов дифференциального исчисления……………………………………….. 3.3. Выпуклые и вогнутые функции. Точки перегиба ……………………… 3.4. Основные теоремы дифференциального исчисления………….............. 3.5. Тождества и неравенства………………………………………………… 3.6. Производные высших порядков…………………………………………. ЗАКЛЮЧЕНИЕ…………………………………………………………………… ОТВЕТЫ И УКАЗАНИЯ………………………………………………………… БИБЛИОГРАФИЧЕСКИЙ СПИСОК……….…………………………...............
|
4 5 8 8 12 18 27
37 44 48 48 51 66 76
76
84 88 95 103 109 112 113 118 |
Учебное издание
Барсуков Андрей Иванович
Глазкова Мария Юрьевна
Минаков Виктор Иванович
ЗАДАЧИ ПОВЫШЕННОЙ СЛОЖНОСТИ
ПО ВЫСШЕЙ МАТЕМАТИКЕ
