
- •Часть 1
- •1. Линейная алгебра
- •1.1. Основные классы квадратных матриц
- •Задачи для самостоятельного решения
- •1.2. Определители. Ранг матрицы
- •1.2.1. Вычисление определителей
- •1.2.2. Вычисление ранга матриц
- •Задачи для самостоятельного решения
- •1.3. Обратная матрица
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Как изменится матрица , если совершить аналогичные преобразования со столбцами матрицы а?
- •1.4. Жорданова нормальная форма
- •1.5. Возведение матриц в степень. Нильпотентные матрицы. След матрицы
- •Задачи для самостоятельного решения
- •1.6. Многочлены
- •Задачи для самостоятельного решения
- •2. Введение в анализ
- •2.1. Метод математической индукции
- •Алгоритм метода математической индукции
- •Решение. Используем метод математической индукции.
- •Задачи для самостоятельного решения
- •2.2. Пределы последовательностей
- •Упражнение 14. Найти
- •Примеры решения задач
- •Пример 2. Пусть , . Найти .
- •Задачи для самостоятельного решения
- •1. Вычислить пределы:
- •2.3. Предел функции. Непрерывность
- •Примеры решения задач
- •Пример 8. Доказать, что если функция непрерывна на отрезке и имеет обратную функцию, то она монотонна на этом отрезке.
- •Задачи для самостоятельного решения
- •3.1. Производная функции. Вычисление производной по определению
- •Если он существует и конечен, называется правосторонней (левосторонней) производной и обозначается . Если существует производная , то будем говорить, что дифференцируема в точке .
- •Теорема 2. Если существует производная , то функция непрерывна в точке .
- •Примеры решения задач Пример 1. Пусть Подобрать коэффициенты a и b так, чтобы функция была дифференцируемой в точке .
- •Заметим, что как произведение бесконечно малой функции на ограниченную , после замены получим
- •Задачи для самостоятельного решения
- •1. Показать, что функция , где – непрерывная функция и , не имеет производной в точке .
- •2. Пусть
- •3.2. Вычисление пределов функций с использованием методов дифференциального исчисления
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •1. Вычислить пределы
- •3.3. Выпуклые и вогнутые функции. Точки перегиба
- •Важную роль при исследовании функции на выпуклость вверх (выпуклость вниз) играют точки, в которых происходит изменение направления выпуклости функции.
- •В этом разделе будут рассмотрены основные свойства выпуклых вниз (вверх) функций, заданных на отрезке .
- •Задачи для самостоятельного решения
- •3.4. Основные теоремы дифференциального исчисления
- •Примеры решения задач
- •Обратим внимание на то, что является точкой перегиба функции . Оказывается, что этот факт верен для любой дважды дифференцируемой функции.
- •Так как , то , что и требовалось доказать.
- •Задачи для самостоятельного решения
- •6. Исследование функции нескольких переменных на экстремум
- •7. Доказательство тождеств с использованием свойств дифференцирования
- •Задачи для самостоятельного решения
- •3.6. Производные высших порядков
- •Задачи для самостоятельного решения
- •Заключение
- •Часть 1
- •394006 Воронеж, ул. 20-летия Октября, 84
6. Исследование функции нескольких переменных на экстремум
Этот метод бывает удобен для доказательства неравенств, зависящих от нескольких параметров.
Доказать неравенство:
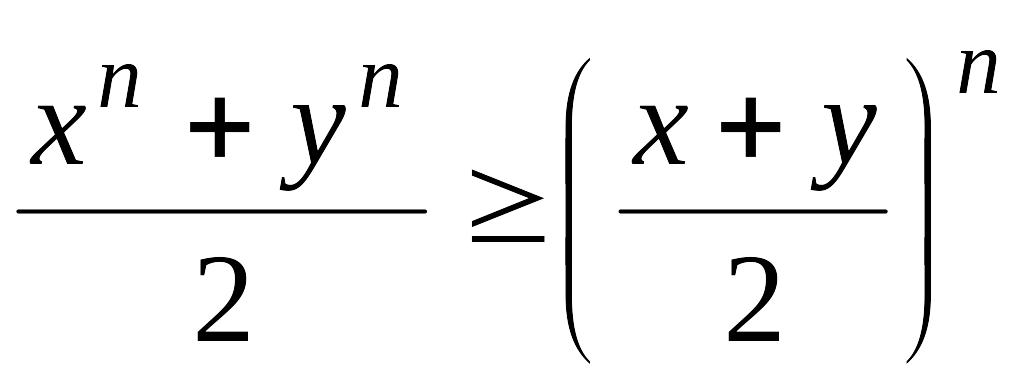 ,
если
,
если
![]() .
.
Решение.
Исследуем
функцию
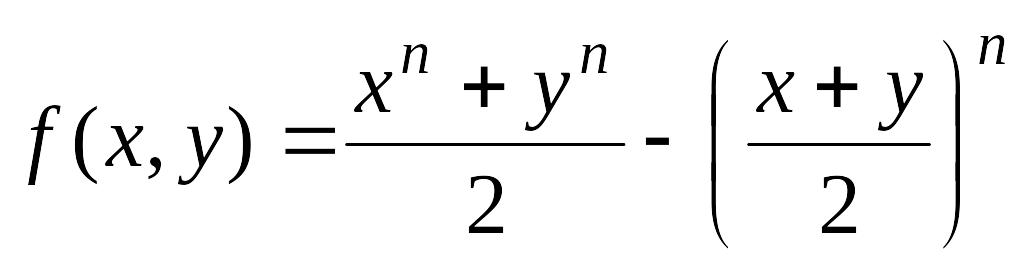 на экстремум:
на экстремум:
а) находим критические точки
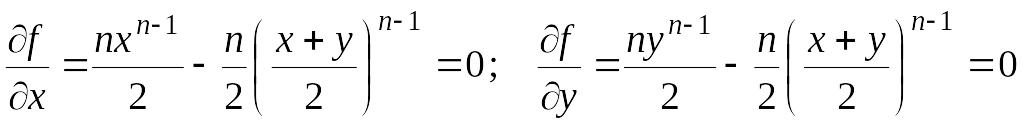 .
.
Отсюда
находим
![]() ;
;
б) исследуем
знак второго дифференциала функции
![]() в точках
:
в точках
:
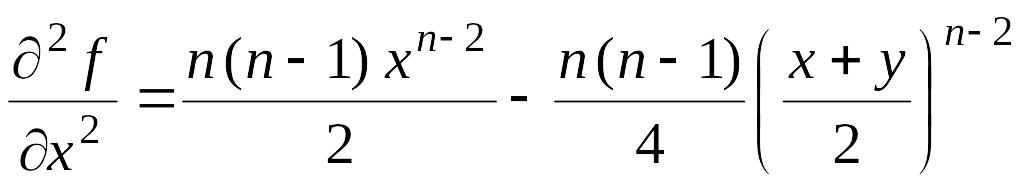 ,
,
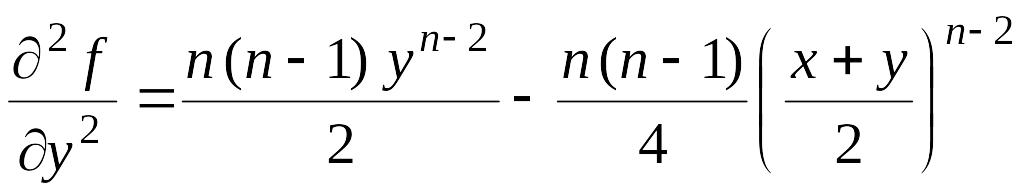 ,
,
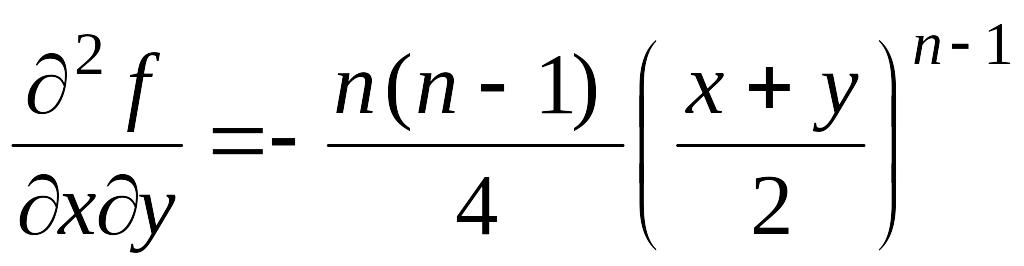 ,
,
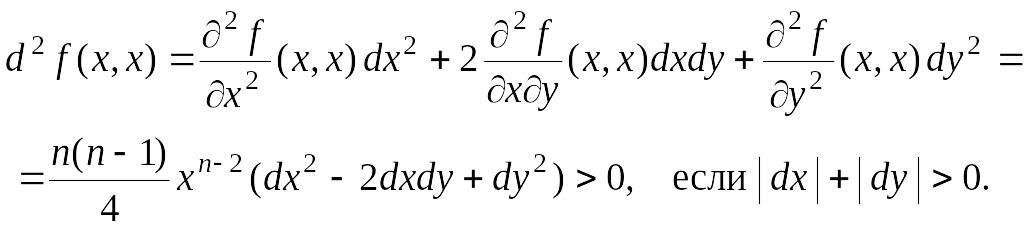
Таким
образом,
![]() – точки минимума функции
.
– точки минимума функции
.
Отсюда получаем
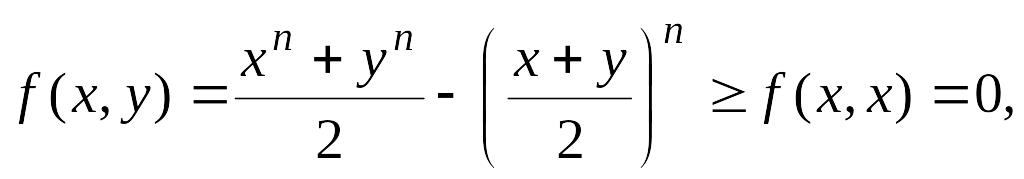
что и требовалось доказать.
7. Доказательство тождеств с использованием свойств дифференцирования
1.
Построить график функции
![]()
Решение. Вычислим производную в точках .
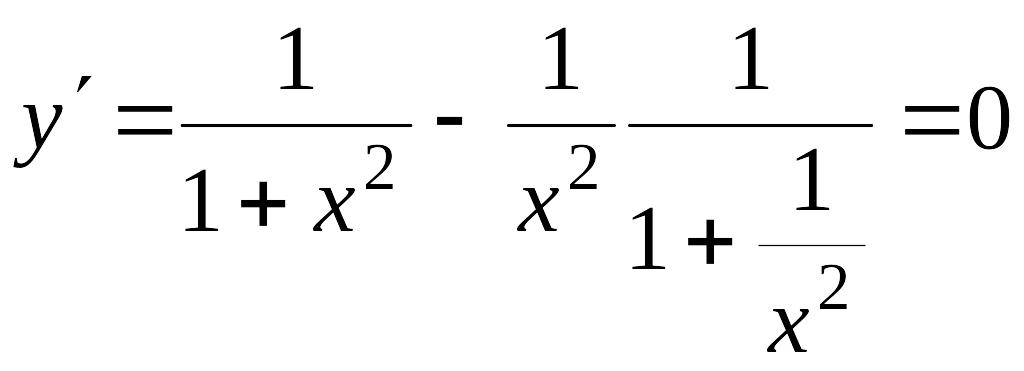 .
.
Так
как
![]() то
то
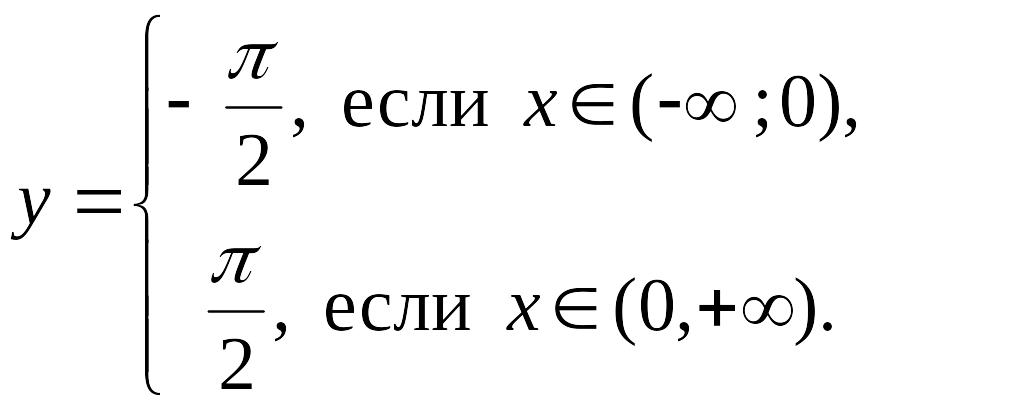
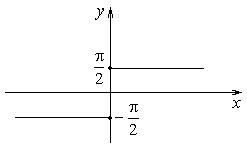
Ответ:
2. Доказать тождество
![]() ,
,
![]() .
.
Решение.
Рассмотрим функцию
![]() ,
.
При
,
.
При
![]() имеем
имеем
![]() .
Пусть
.
Пусть
![]() ;
тогда
;
тогда
![]() и
и

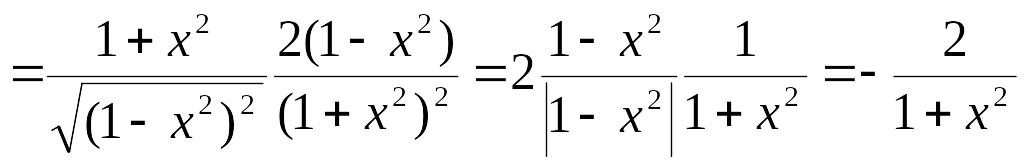 .
.
Поэтому
![]() ,
.
Следовательно, функция при
является тождественно равной постоянной.
Чтобы найти эту постоянную, вычислим,
например,
,
.
Следовательно, функция при
является тождественно равной постоянной.
Чтобы найти эту постоянную, вычислим,
например,
![]() ;
имеем:
;
имеем:
 .
Таким образом, тождество доказано.
.
Таким образом, тождество доказано.
Задачи для самостоятельного решения
1. Доказать тождества:
а)
![]()
=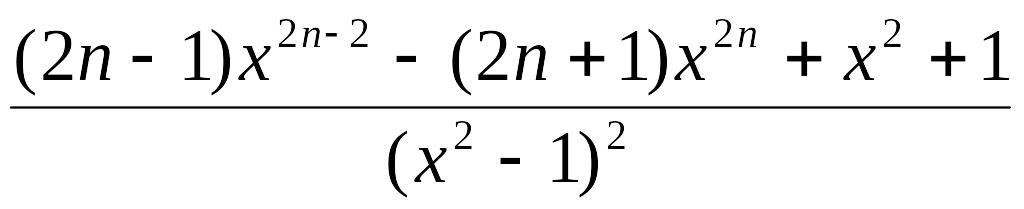 ,
,
![]() ;
;
б)
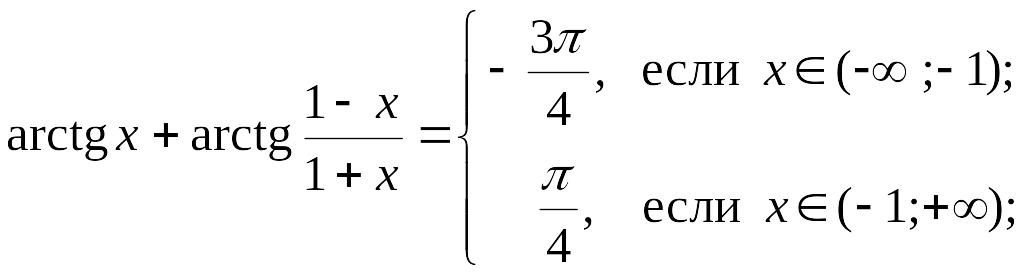
в)
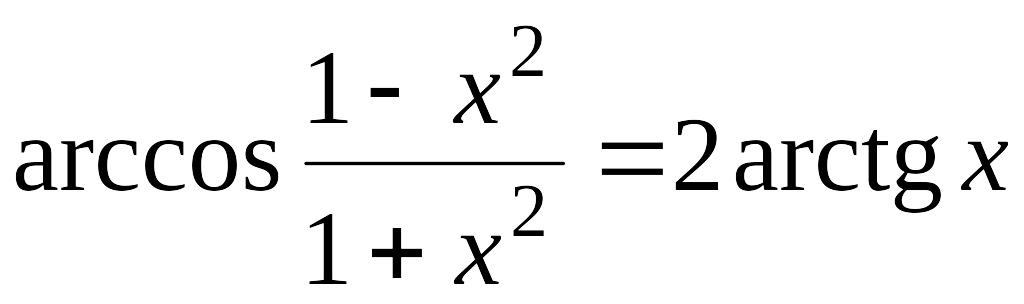 при
при
![]() ;
;
г)
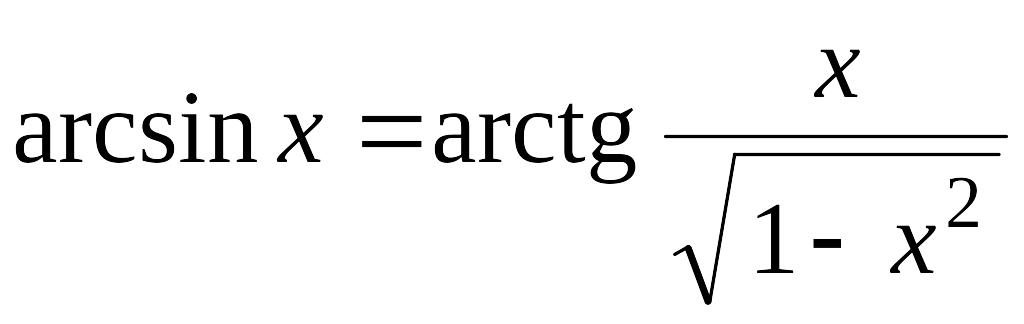 при
при
![]() .
.
2. Доказать неравенства:
а)
![]() при
;
б)
при
;
б)
![]() ;
;
в)
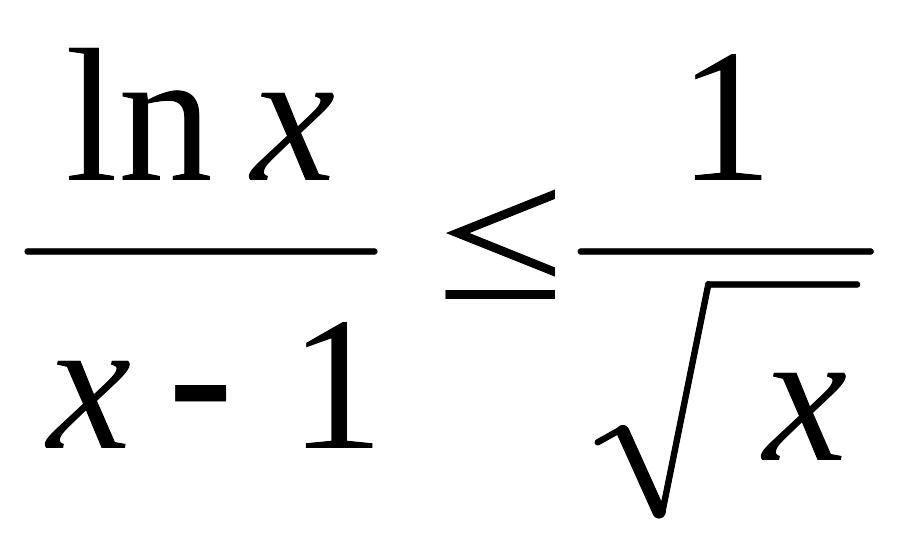 при
при
![]() ;
г)
;
г)
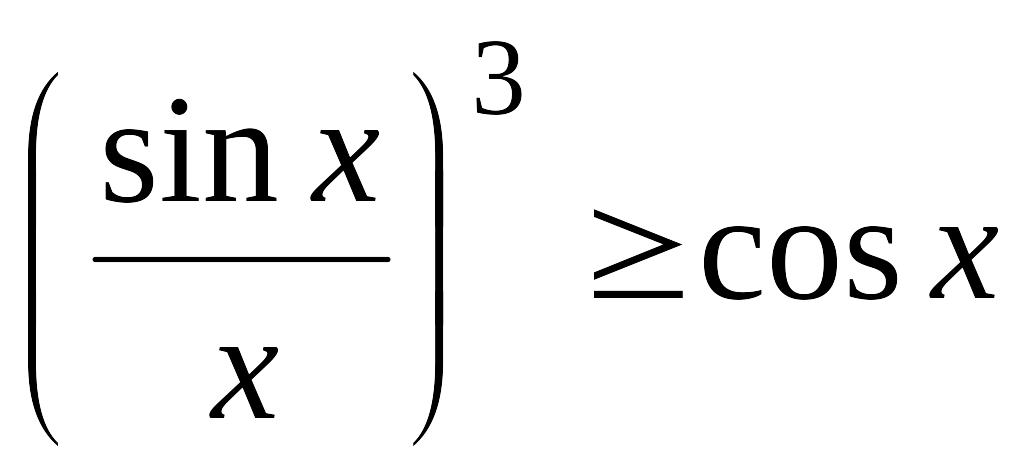 при
при
![]() ;
;
д)
 при
при
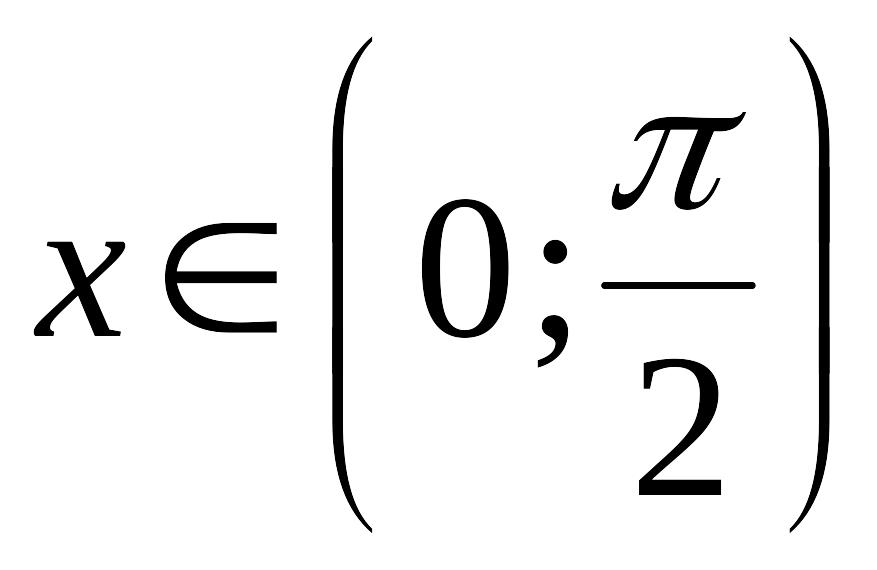 ;
;
е)
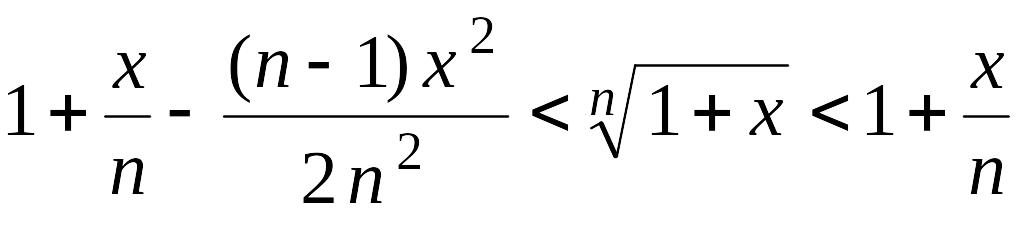 при
при
![]() ;
;
ж)
![]() ,
,
![]() .
.
3. Доказать неравенства:
а)
![]() при
при
![]() ;
б)
;
б)
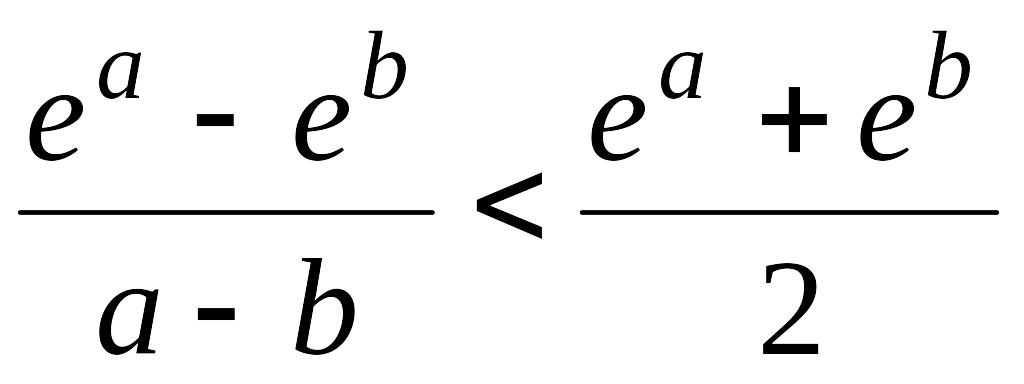 при
при
![]() ;
;
в)
![]() при
при
![]() ,
,
г)
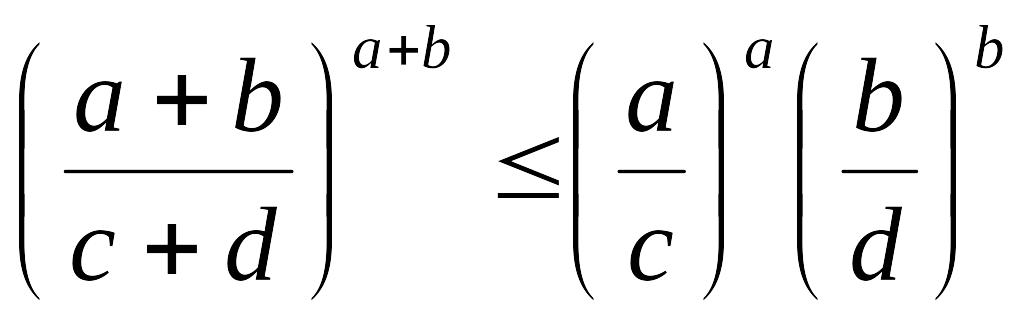 ,
где
,
где
![]() −
произвольные положительные числа,
−
произвольные положительные числа,
д)
![]() ,
где
,
где
![]() −
произвольные положительные числа.
−
произвольные положительные числа.
4. Найти
наибольшее и наименьшее значения функции
![]() в области
в области
![]() .
.
3.6. Производные высших порядков
Производная
![]() данной
дифференцируемой функции y
= f(x),
называемая производной первого порядка,
представляет собой некоторую новую
функцию. Возможно, что эта функция сама
имеет производную.
данной
дифференцируемой функции y
= f(x),
называемая производной первого порядка,
представляет собой некоторую новую
функцию. Возможно, что эта функция сама
имеет производную.
Определение
1. Производная
от производной первого порядка называется
производной второго порядка или второй
производной и обозначается так:
![]() или
или
![]()
Аналогично
если существует производная от производной
второго по− рядка, то она называется
производной третьего порядка или третьей
произ− водной и обозначается так:
![]() или
или
![]() и
т.д.
и
т.д.
Пример
1.
![]() ,
найти
,
найти
![]() .
.
Решение. Преобразуем выражение к виду
![]() .
.
Так как
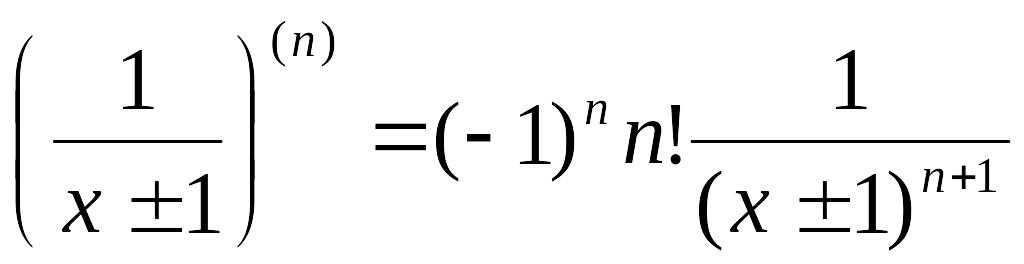 ,
,
то
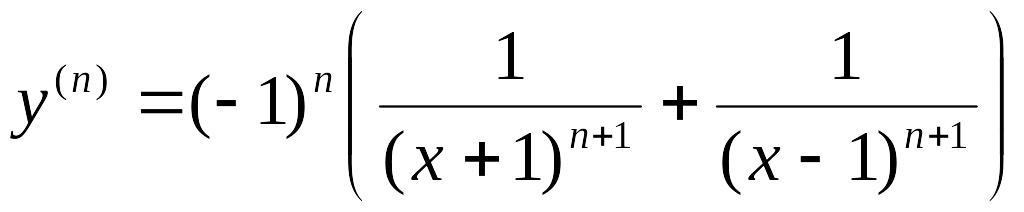 .
.
Пусть
![]() и
и
![]() имеют
производные до n-го
порядка включительно.
имеют
производные до n-го
порядка включительно.
Тогда
для производной n-го
порядка их произведения
![]() справедлива формула
Лейбница
справедлива формула
Лейбница
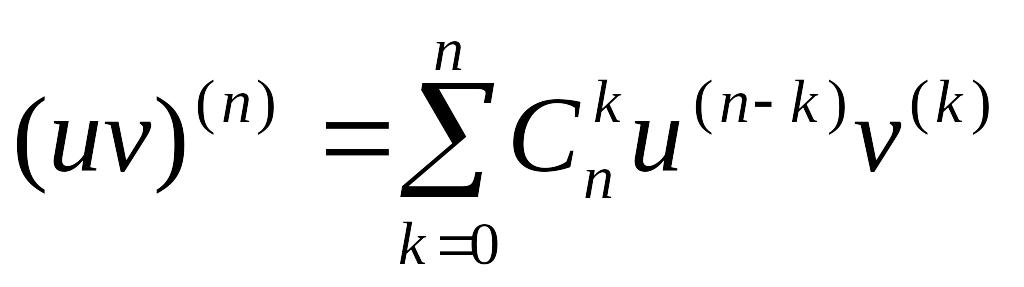 .
.
Пример 2. Вычислить значение n-й производной функции
![]() в
точке
.
в
точке
.
Решение. По условию имеем
![]() .
.
Продифференцируем
это тождество n
раз, применяя формулу Лейбница. Тогда
![]() получим
получим
![]() ,
,
откуда при
![]() ,
,
или
![]() .
.
Получили
рекуррентную формулу для определения
n-й
производной в точке
(
).
Значения
![]() и
и
![]() найдем непосредственно:
найдем непосредственно:
![]() ,
,
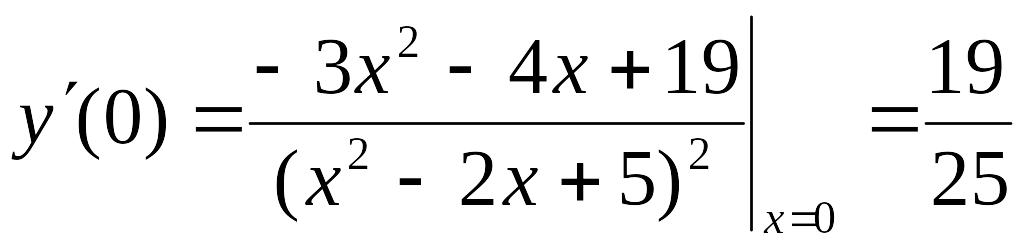 .
.
Затем, полагая последовательно n=2, 3, 4, …, с помощью рекуррентной формулы получим значения производных высших порядков.
Пример
3. Найти
производную второго порядка от функции,
заданной параметрически:
![]() ,
,
![]() ,
,
![]() .
.
Решение. Имеем
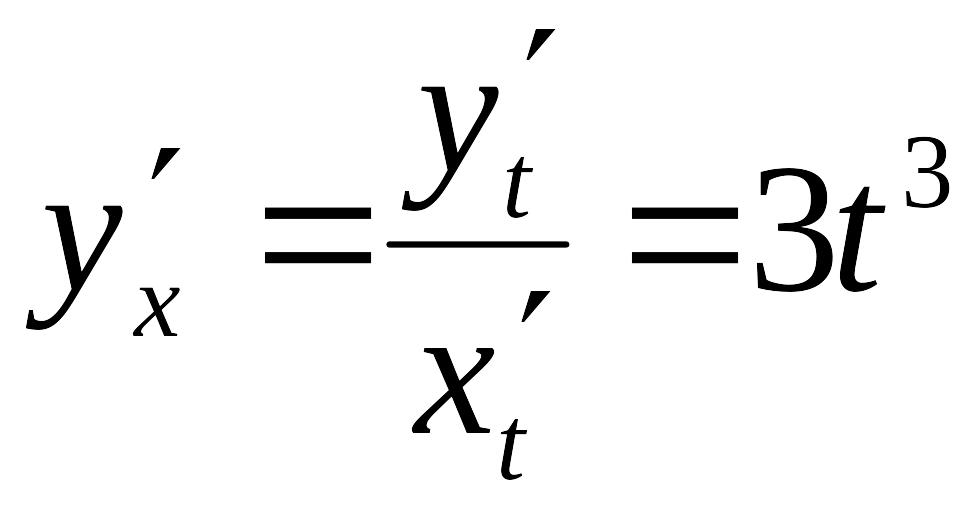 и
и
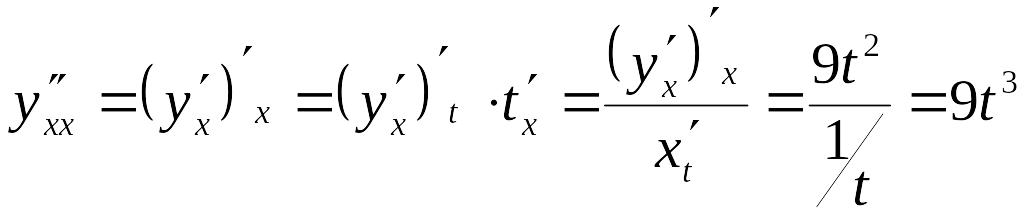 .
.
Заметим,
что в данном случае параметр t
легко исключить из заданных уравнений,
полагая
![]() .
.
В
общем случае, если
![]() ,
,
![]() ,
то
,
то
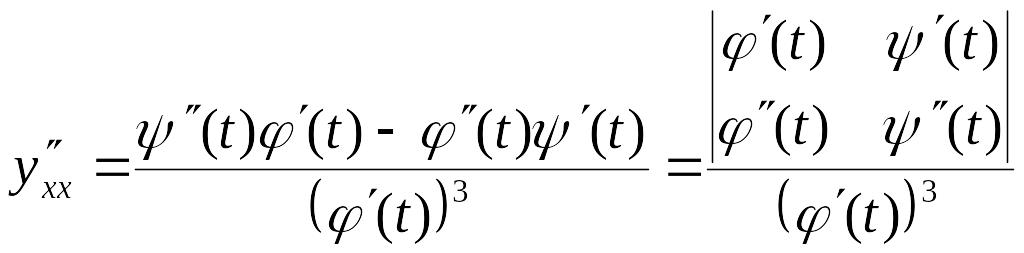 .
.
