Так как , то , что и требовалось доказать.
2.
Возьмем
при
.
Тогда неравенство
выполнено для всех
и
.
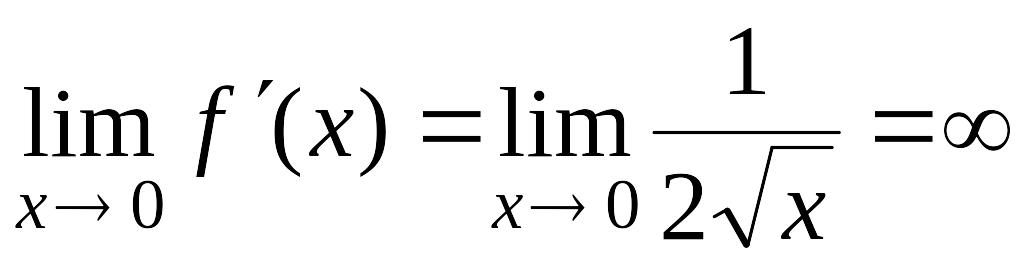П
р и м е р 8. Пусть
функция
дифференцируема на
и равенство
(3.4)
справедливо
для некоторого
и всех
.
Тогда
,
где
.
Решение. Из равенства (3.4), записанного в виде
,
следует,
что тангенс угла между хордой, соединяющей
точки
и
,
и положительным направлением оси
равен
.
Так как любая точка графика функции
представима в виде
,
то график этой функции совпадает с
прямой, проходящей через точку
и имеющей угловой коэффициент
.
Таким образом,
.
П
р и м е р 9.
Пусть
бесконечно дифференцируема на ин-тервале
и существует
такая, что
для всех
и
.
Показать, что удовлетворяет одному из следующих условий:
1) – точка строгого экстремума;
2) – точка перегиба;
3)
является константой на
.
Решение. 1. Предположим, что
и
– четное число.
Тогда
.
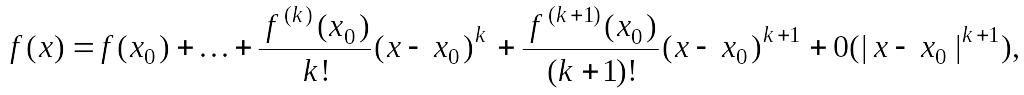
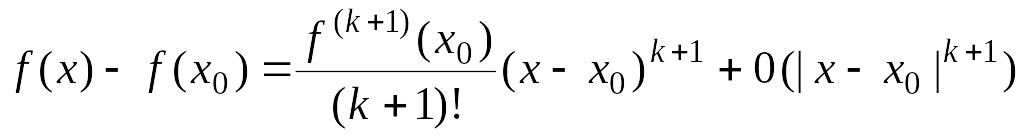Так как
сохраняет знак на
и
,
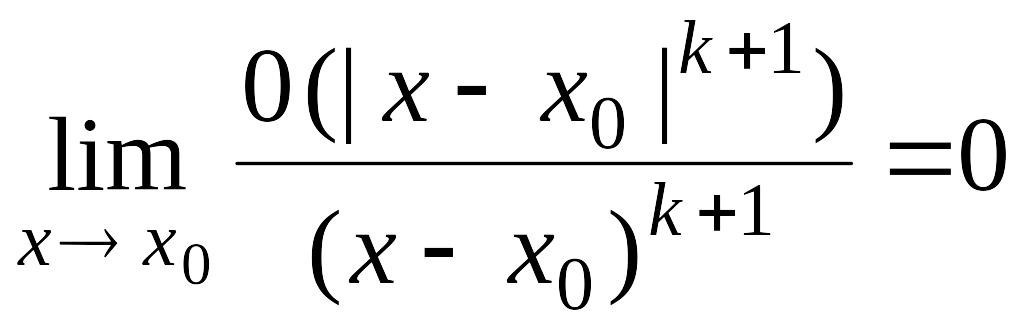то найдется окрестность точки
,
в которой выполнено равенство
,
то есть:
–
точка максимума, если
;
– точка минимума, если
.
2. Предположим, что
и – нечетное число. Тогда, используя разложение по формуле Тейлора функции
в
точке
,
получаем
.
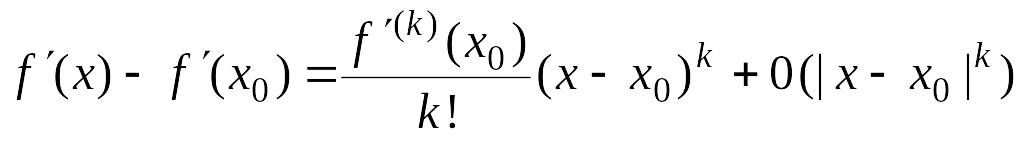Так
как
–
четное число, то
– точка экстремума функции
и, следовательно,
является точкой перегиба графика функции
.
3.
для всех
.
Тогда
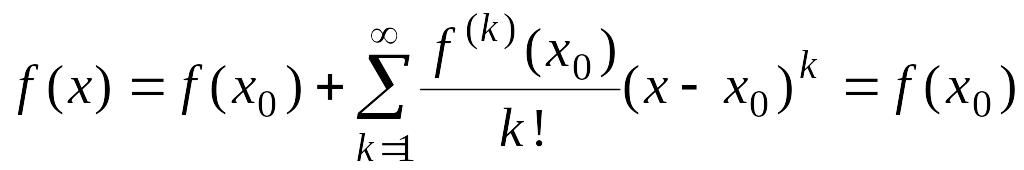для
всех
.
Задачи для самостоятельного решения
1.
Найти на кривой
точку, касательная в которой параллельна
хорде, соединяющей точки
и
.
2.
Найти функцию
такую, что
если
.
3. Доказать неравенства:
а)
;
б)
;
в)
,
если
.
4. Доказать, что единственная функция, имеющая постоянную производную на , есть линейная функция
.
5. Пусть – четная функция, определенная на и имеющая в точке все производные. Доказать, что
для
всех
.
6.
Функция
дифференцируема на
,
причем выполнены условия:
для некоторого
.
Доказать, что выполняется тождество
.
7. Показать, что если кривая пересекает некоторую прямую в трех точках, то между крайними точками пересечения находится по крайней мере одна точка перегиба кривой.
8.
Функция
имеет на полуоси
непрерывную производную,
для всех
.
Доказать, что существует такая точка
,
что
.
9.
Пусть функция
дифференцируема на отрезке
.
Доказать, что
.
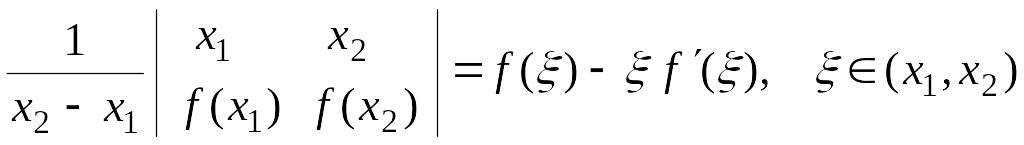10. Определить число вещественных корней уравнения:
а)
б)
в)
11.
Используя
результат, сформулированный в примере
2, доказать теорему
Дарбу:
если функция
имеет конечную производную на отрезке
,
то функция
принимает
в качестве значения каждое промежуточное
число между
и
.
12.
Доказать, что всякая монотонная на
функция
непрерывна на
.
13.
Обозначим
через f
функцию, определенную на отрезке
и выпуклую, а через
(i=1,
2, …, n)
− строго положительные числа и
.
Показать, что
.
14.
Показать,
что если
,
то функция f
, определенная
для
равенством
,
выпуклая, и доказать, что если
− строго положительные числа, то
.
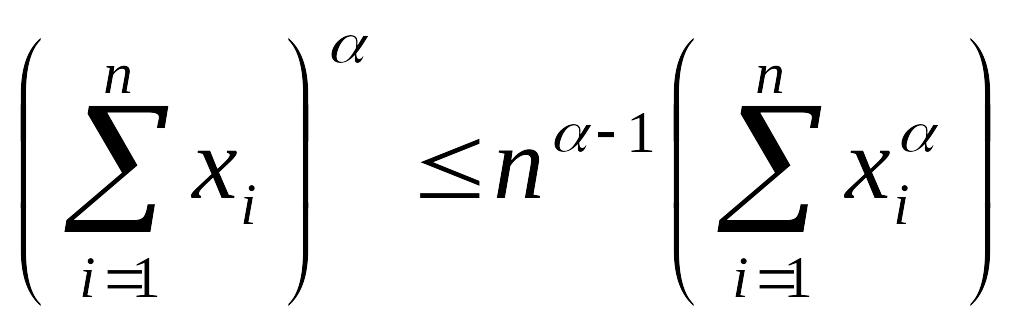Может ли здесь достигаться равенство?
3.5. Тождества и неравенства
1. Применение метода математической индукции
к доказательству неравенств
Доказать неравенство:
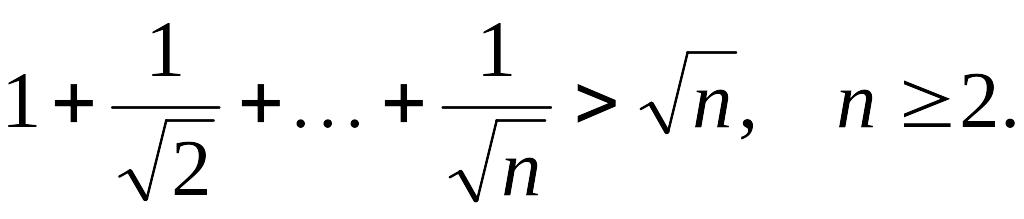
Решение:
а)
если
,
то
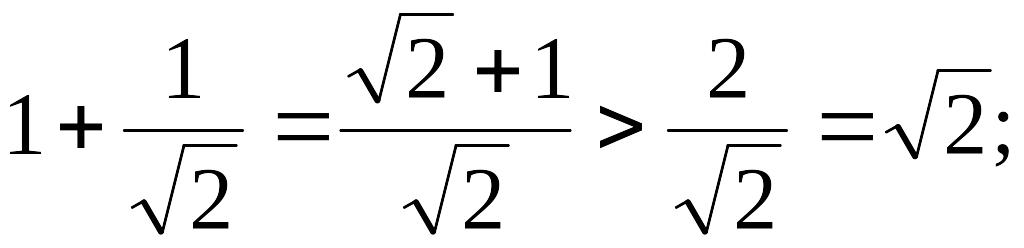
б) предположим, что рассматриваемое неравенство верно для некоторого ;
в)
покажем, что
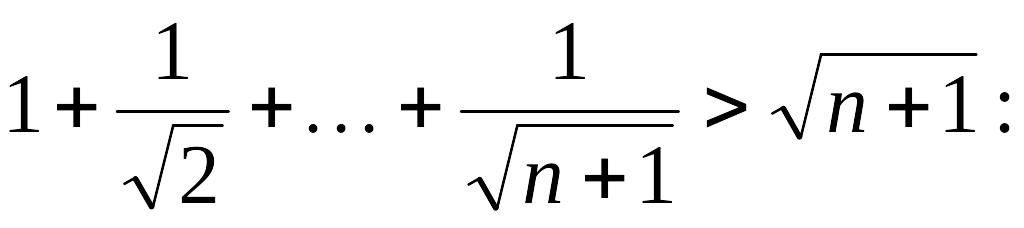
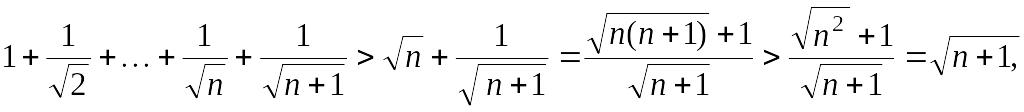
что и требовалось доказать.
2. Использование монотонности функции
Доказать двойное неравенство:
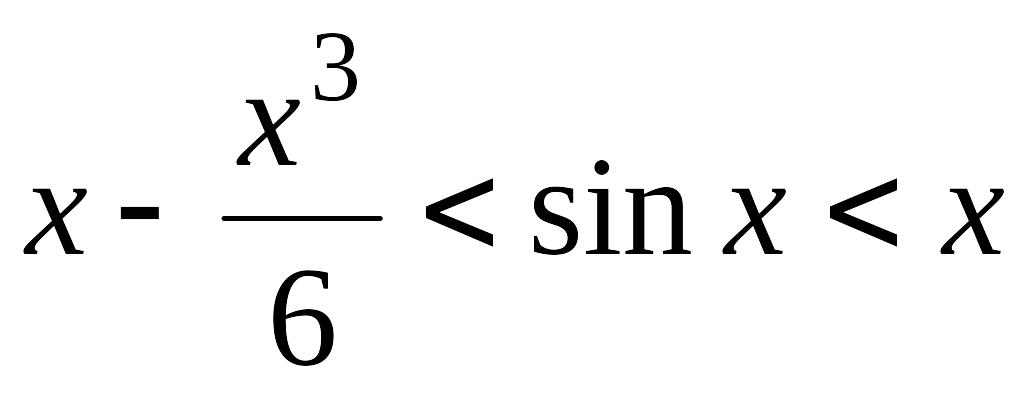при
Доказательство.
Рассмотрим
функцию
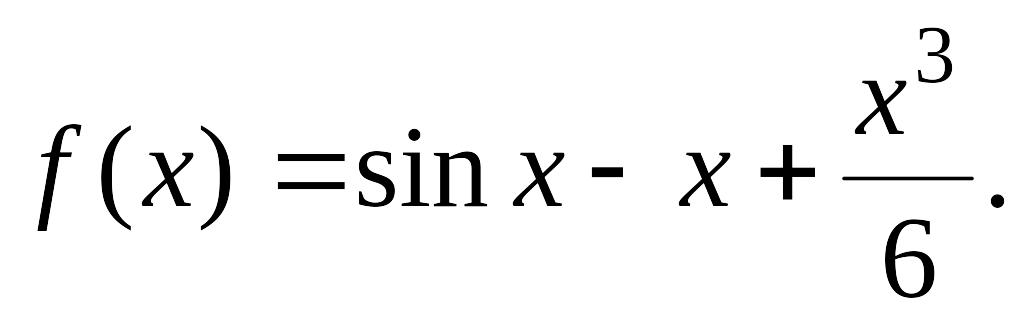
Заметим,
что а)
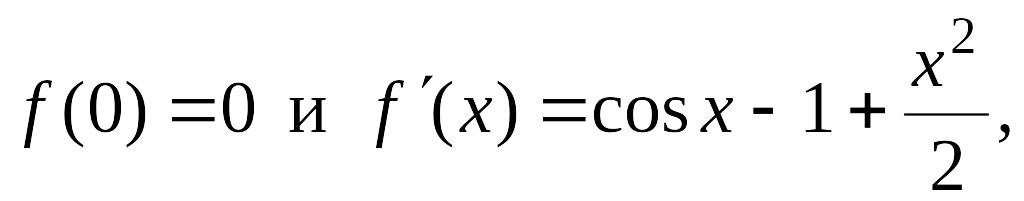
б)
в)
Из
в
следует, что
при
,
затем из б
следует, что
при
,
и, наконец, из а
следует, что
при
.
Аналогично доказывается второе неравенство.
3. Использование экстремальных свойств функций
Доказать неравенство:
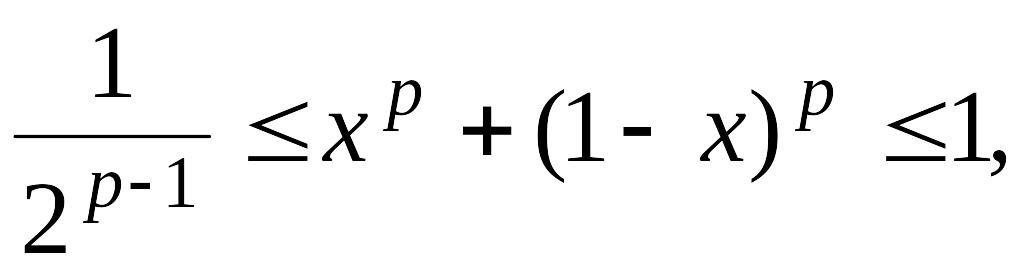если
.
Решение.
Найдем
наименьшее и наибольшее значение функции
:
.
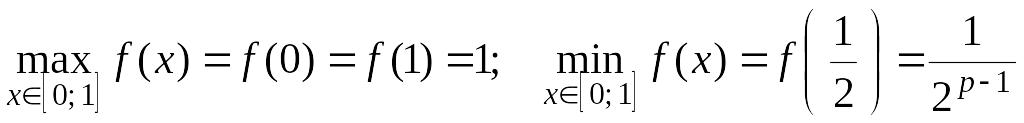Отсюда
следует, что при
.
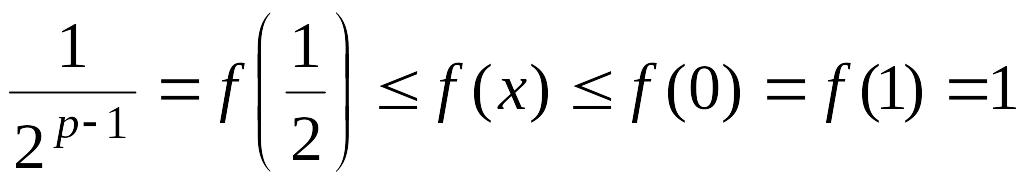4. Использование направления выпуклости функций
Доказать неравенство:
при
Решение. Разделим обе части неравенства на 2:
и
рассмотрим функцию
,
Так как
и
при
,
то
выпукла вниз на
.
Значит,
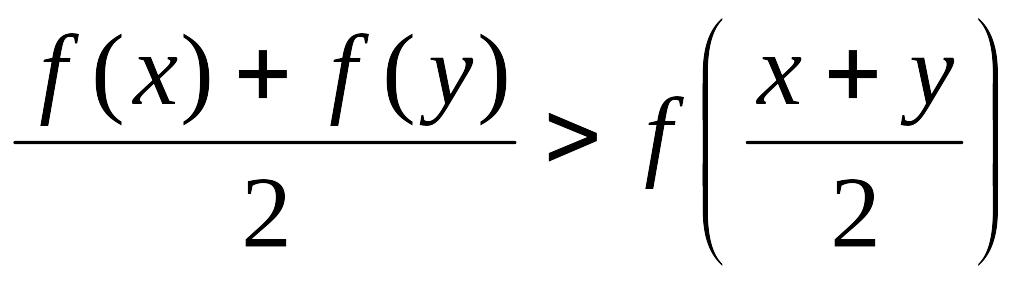при
,
что и требовалось доказать.
Замечание. Другие примеры неравенств, вытекающих из определения выпуклости вверх (выпуклости вниз) были приведены в конце раздела 3.3.
Переход от дискретного параметра
к
непрерывному параметру
Этот прием является весьма эффективным, так как сводит исследование последовательностей к исследованию функций, что позволяет применять правило Лопиталя, нахождение экстремумов с помощью производных и т.д.
Пример1.
Установить,
является ли монотонной числовая
последовательность
.
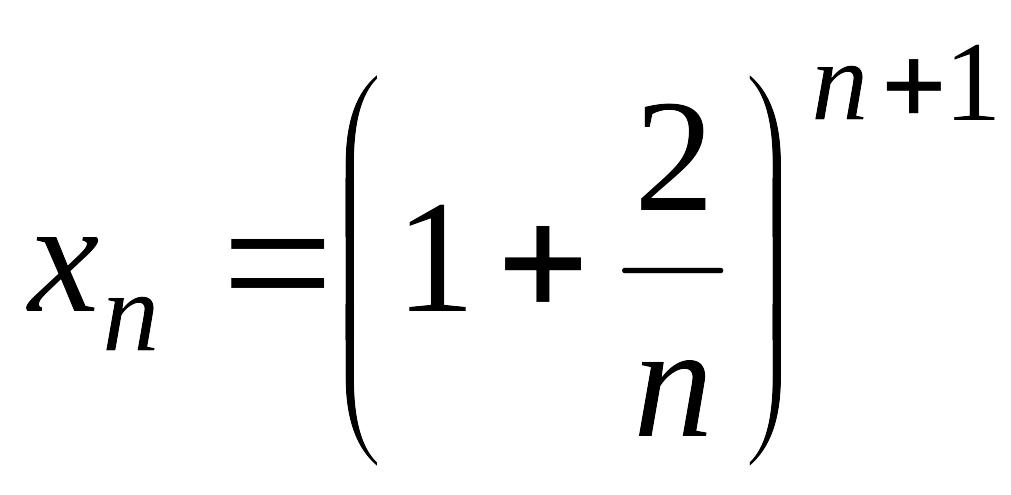Решение.
Исследуем
функцию
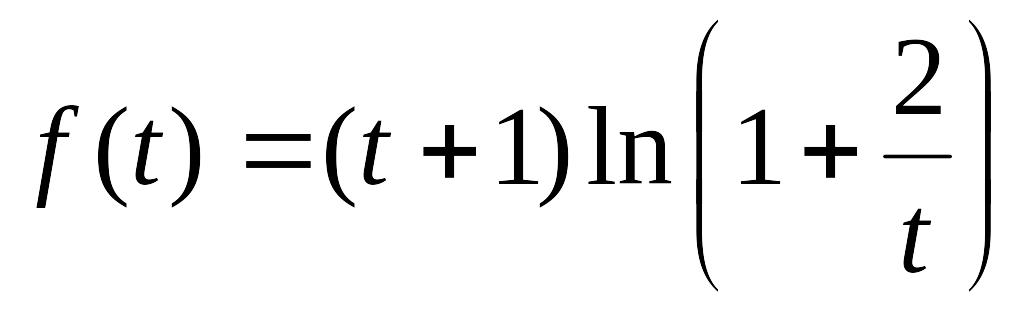на монотонность при
.
Для этого рассмотрим
.
,
.
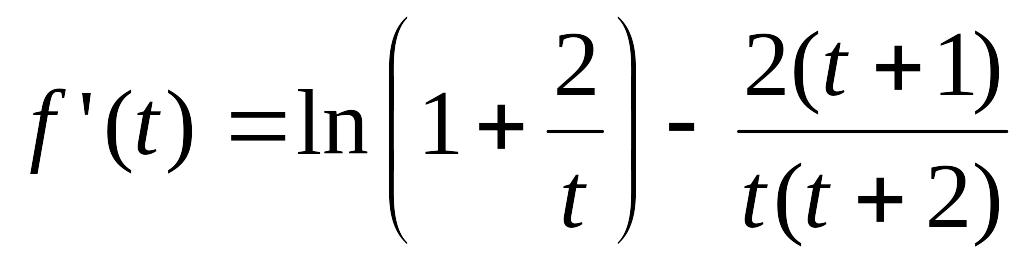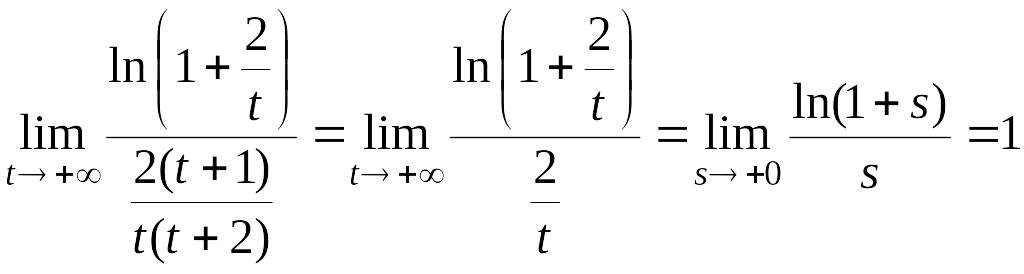Отсюда
следует, что
.
Так
как
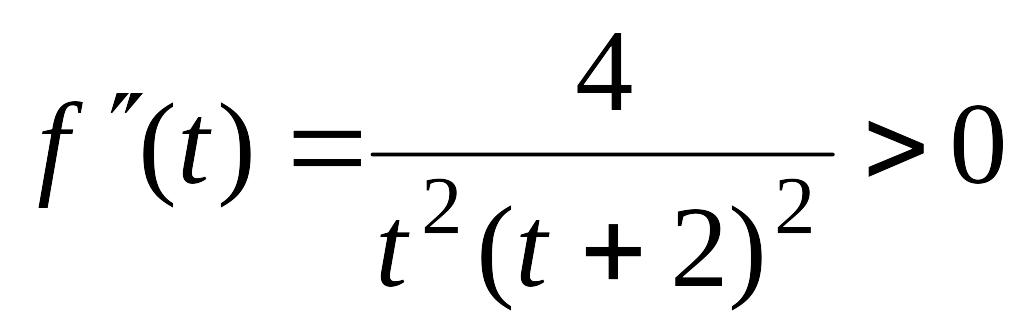для всех
,
то
возрастает на
.
С учетом равенства
это означает, что
для всех
.
Значит,
и
убывают на
.
Таким образом,
.