1.1. Основные классы квадратных матриц
Рассмотрим некоторые классы квадратных матриц, которые часто являются объектом исследования в линейной алгебре. Символ А-1 обозначает матрицу, обратную матрице А ( А-1А=АА-1=Е, Е – единичная матрица).
Матрица
А называется симметрической,
если
.
Матрица
А называется кососимметрической,
если
.
Матрица
А называется эрмитовой,
если
.
Матрица
А называется косоэрмитовой,
если
.
Матрица
А называется ортогональной,
если
.
Матрица
А называется унитарной,
если
.
Матрица
А называется нормальной,
если
.
Матрица
А называется нильпотентной,
если
для некоторого
.
Матрица А называется верхней (нижней) треугольной, если все ее элементы, расположенные под (над) главной диагональю, равны нулю.
Матрица А называется положительной (неотрица-тельной), если все ее элементы положительные (неотрицательные) числа.
Матрица
А называется положительно
(неотрицатель-но)
определенной,
если
для всех
.
Непосредственно из определения следует утверждение о структуре описанных выше классов матриц.
Утверждение
1. Пусть
.
Тогда имеют место следующие эквивалентности:
1)
2)
в частности
3)
4)
в частности
5)
строки
(столбцы)
матрицы
являются попарно ортогональными
векторами, модуль которых равен единице.
Введенные классы матриц позволяют провести аналогию между матрицами и комплексными числами.
Каждая матрица представима двумя следующими способами:
1)
где
;
2)
– неотрицательно
определенная,
–
унитарная матрица.
Представление 1 является матричным аналогом алгебраической формы записи комплексного числа:
где
Представление 2 является матричным аналогом показательной формы записи комплексного числа:
(сравнить
с
).
Более того,
,
что является аналогом формулы для модуля
комплексного числа
матрица
представима в виде
где
– эрмитова матрица, то есть
аналогично равенству
.
Правило построения матричной степени
будет объяснено ниже.
Рассмотрим, каким образом операция сопряжения, свойства эрмитовости и унитарности матриц могут быть описаны при помощи скалярного произведения.
Утверждение
2. Для
любой квадратной матрицы
порядка
и векторов
выполнено
равенство
В
частности, если
,
то
.
Доказательство.
Обозначим
Тогда по правилу умножения вектора на
матрицу и определению скалярного
произведения получаем:
1)
;
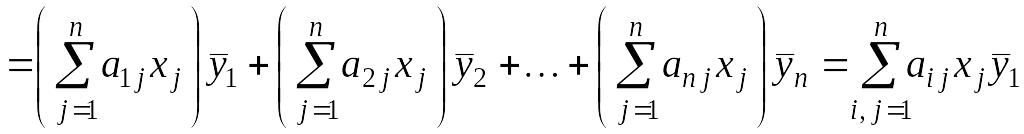2)
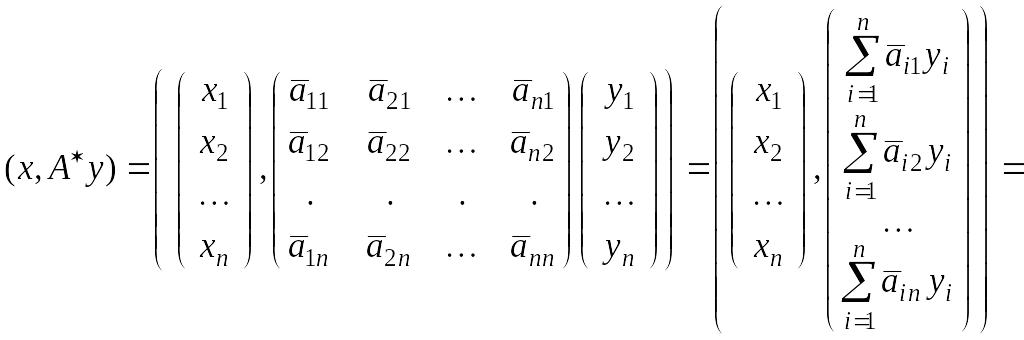
Сопоставив 1 и
2, получаем равенство
.
Утверждение
3. Если
– унитарная матрица порядка
,
то для любого
выполнено равенство
.
Доказательство:
Здесь первое равенство вытекает из
утверждения 1, второе равенство – из
определения унитарной матрицы.
Задачи для самостоятельного решения
1. Найти все симметрические ортогональные и кососимметрические ортогональные матрицы порядка 2.
2. Найти все квадратные матрицы, коммутирующие со всеми матрицами того же порядка.
3. Доказать,
что если
нильпотентная
матрица порядка 2, то
.
4. Показать,
что если
,
то
5. При каком
условии матрица
является нормальной, где
– квадратные матрицы произвольного
одинакового порядка.
6. Показать, что
а)
б)
7. Показать, что вещественная унитарная матрица является ортогональной. Привести пример комплексной ортогональной матрицы, которая не является унитарной.
8. При каких условиях диагональная матрица является ортогональной (унитарной)?
9. Проверить, что любое из следующих трех свойств квадратной мат-рицы: вещественность, ортогональность, унитарность – вытекает из двух других.