
- •Часть 1
- •1. Линейная алгебра
- •1.1. Основные классы квадратных матриц
- •Задачи для самостоятельного решения
- •1.2. Определители. Ранг матрицы
- •1.2.1. Вычисление определителей
- •1.2.2. Вычисление ранга матриц
- •Задачи для самостоятельного решения
- •1.3. Обратная матрица
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Как изменится матрица , если совершить аналогичные преобразования со столбцами матрицы а?
- •1.4. Жорданова нормальная форма
- •1.5. Возведение матриц в степень. Нильпотентные матрицы. След матрицы
- •Задачи для самостоятельного решения
- •1.6. Многочлены
- •Задачи для самостоятельного решения
- •2. Введение в анализ
- •2.1. Метод математической индукции
- •Алгоритм метода математической индукции
- •Решение. Используем метод математической индукции.
- •Задачи для самостоятельного решения
- •2.2. Пределы последовательностей
- •Упражнение 14. Найти
- •Примеры решения задач
- •Пример 2. Пусть , . Найти .
- •Задачи для самостоятельного решения
- •1. Вычислить пределы:
- •2.3. Предел функции. Непрерывность
- •Примеры решения задач
- •Пример 8. Доказать, что если функция непрерывна на отрезке и имеет обратную функцию, то она монотонна на этом отрезке.
- •Задачи для самостоятельного решения
- •3.1. Производная функции. Вычисление производной по определению
- •Если он существует и конечен, называется правосторонней (левосторонней) производной и обозначается . Если существует производная , то будем говорить, что дифференцируема в точке .
- •Теорема 2. Если существует производная , то функция непрерывна в точке .
- •Примеры решения задач Пример 1. Пусть Подобрать коэффициенты a и b так, чтобы функция была дифференцируемой в точке .
- •Заметим, что как произведение бесконечно малой функции на ограниченную , после замены получим
- •Задачи для самостоятельного решения
- •1. Показать, что функция , где – непрерывная функция и , не имеет производной в точке .
- •2. Пусть
- •3.2. Вычисление пределов функций с использованием методов дифференциального исчисления
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •1. Вычислить пределы
- •3.3. Выпуклые и вогнутые функции. Точки перегиба
- •Важную роль при исследовании функции на выпуклость вверх (выпуклость вниз) играют точки, в которых происходит изменение направления выпуклости функции.
- •В этом разделе будут рассмотрены основные свойства выпуклых вниз (вверх) функций, заданных на отрезке .
- •Задачи для самостоятельного решения
- •3.4. Основные теоремы дифференциального исчисления
- •Примеры решения задач
- •Обратим внимание на то, что является точкой перегиба функции . Оказывается, что этот факт верен для любой дважды дифференцируемой функции.
- •Так как , то , что и требовалось доказать.
- •Задачи для самостоятельного решения
- •6. Исследование функции нескольких переменных на экстремум
- •7. Доказательство тождеств с использованием свойств дифференцирования
- •Задачи для самостоятельного решения
- •3.6. Производные высших порядков
- •Задачи для самостоятельного решения
- •Заключение
- •Часть 1
- •394006 Воронеж, ул. 20-летия Октября, 84
Задачи для самостоятельного решения
1. Используя определение выпуклости вверх (выпуклости вниз), показать, что
а) функция
![]() –
выпукла вверх на промежутке
–
выпукла вверх на промежутке
![]() и выпукла вниз на промежутке
и выпукла вниз на промежутке
![]() ;
;
б) функция
![]() –
выпукла вниз на
;
–
выпукла вниз на
;
в) функция
![]() – выпукла вверх на промежутке
– выпукла вверх на промежутке
![]() .
.
2. Всегда ли произведение двух выпуклых вверх функций является функцией выпуклой вверх?
3. Функция
![]() непрерывно дифференцируема и выпукла
вверх на
непрерывно дифференцируема и выпукла
вверх на
![]() .
Известно, что
.
Известно, что
![]() существует и конечен. Доказать, что
существует и конечен. Доказать, что
![]() .
.
4. Непрерывная
функция
выпукла вниз на
,
![]() и
и
![]() .
Доказать, что при
функция
.
Доказать, что при
функция
![]() возрастает.
возрастает.
5. Привести
пример выпуклых вниз на
функций
и
таких, что
![]()
6. Найти промежутки выпуклости вверх (выпуклости вниз) и точки перегиба графиков следующих функций:
а)
![]() б)
б)
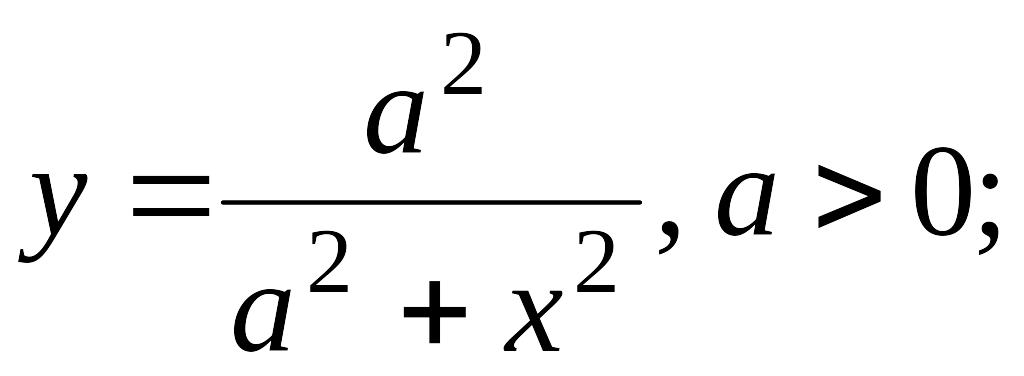 в)
в)
![]() .
.
7. При каком значении параметра кривая
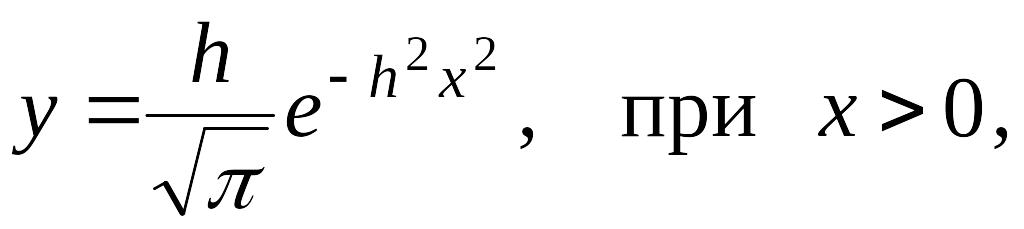
имеет точки
перегиба с абсциссами
![]() ,
где
– произвольное заданное число?
,
где
– произвольное заданное число?
8. Доказать,
что кривая
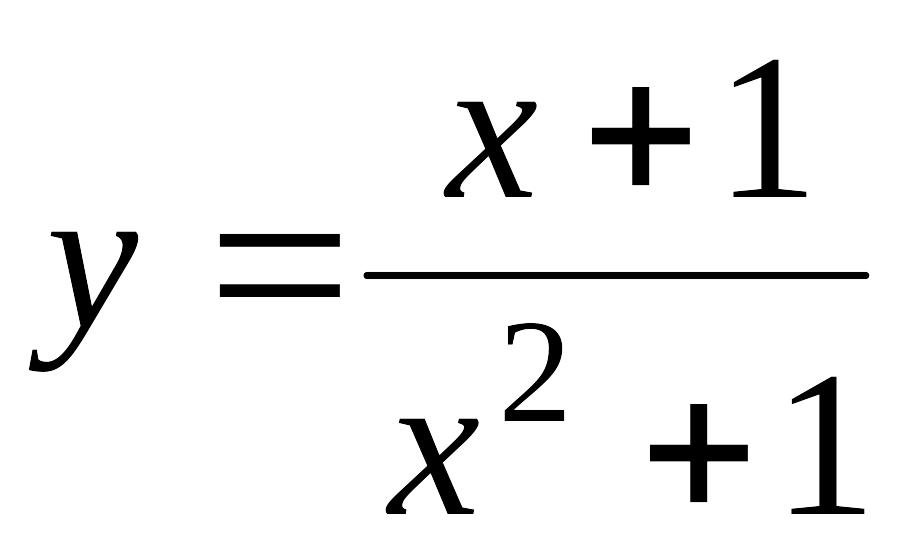 имеет три точки перегиба, лежащие на
одной прямой.
имеет три точки перегиба, лежащие на
одной прямой.
9. Доказать,
что если функция
![]() является выпуклой вниз и возрастает на
интервале
является выпуклой вниз и возрастает на
интервале
![]() ,
а функция
выпуклая вниз на интервале
,
а функция
выпуклая вниз на интервале
![]() ,
то сложная функция
,
то сложная функция
![]() является выпуклой вниз на интервале
.
является выпуклой вниз на интервале
.
3.4. Основные теоремы дифференциального исчисления
Рассмотрим основные теоремы анализа, относящиеся к операции дифференцирования. К таковым традиционно относят следующие теоремы.
Теорема
Ферма. Пусть
функция
![]() определена
в интервале
определена
в интервале
![]() и в точке
и в точке
![]() принимает
наибольшее (наименьшее)
значение. Если существует производная,
то необходимо, чтобы
принимает
наибольшее (наименьшее)
значение. Если существует производная,
то необходимо, чтобы
![]() .
.
Теорема Ролля. Пусть функция :
1) определена и непрерывна на отрезке ;
2)
дифференцируема в интервале
![]() ;
;
3)
![]() .
.
Тогда найдется точка такая, что .
Теорема Лагранжа. Пусть функция :
1) определена и непрерывна на отрезке ;
2) дифференцируема в интервале .
Тогда найдется точка такая, что
![]() .
.
Теорема
Коши. Пусть
функции
и
![]() :
:
1) определены и непрерывны на отрезке ;
2) дифференцируемы в интервале ;
3)
для всех
![]() .
.
Тогда найдется точка такая, что
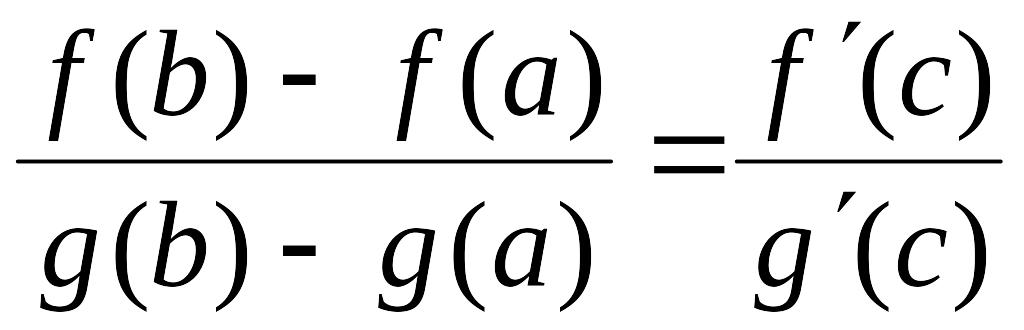 .
.
Примеры решения задач
Пример1.
Пусть полином
![]() имеет n
различных
вещественных
корней. Показать, что полином
имеет n
различных
вещественных
корней. Показать, что полином
![]() имеет
вещественных корней.
имеет
вещественных корней.
Решение.
Пусть
![]() – корни полинома
– корни полинома
![]() .
Тогда
.
Тогда
![]() для всех
для всех
![]() .
Применив теорему Ролля к функции
на каждом из отрезков
.
Применив теорему Ролля к функции
на каждом из отрезков
![]() ,
получим, что существуют
точек
,
получим, что существуют
точек
![]() ,
для которых
,
для которых
![]() .
.
Пример2.
Пусть
дифференцируема на отрезке
![]() и
и
![]() .
Доказать, что на интервале
.
Доказать, что на интервале
![]() найдется точка
найдется точка
![]() такая, что
.
такая, что
.
Решение.
Функция
непрерывна на отрезке
,
и, значит, по теореме 7 раздела 3.3 найдутся
точки
![]() такие, что
такие, что
![]()
Так
как
![]() принимает на отрезке
значения разных знаков, то функция
не является монотонной на
.
Значит, по крайней мере одна из точек
принимает на отрезке
значения разных знаков, то функция
не является монотонной на
.
Значит, по крайней мере одна из точек
![]() (скажем,
(скажем,
![]() )
не совпадает с концами отрезка
.
По теореме Ферма
)
не совпадает с концами отрезка
.
По теореме Ферма
![]() .
.
Очевидно, что если
условия теоремы Лагранжа выполнены на
отрезке
,
то они будут выполнены на каждом отрезке
![]() . Таким образом, каждой паре точек
. Таким образом, каждой паре точек
![]() ставится в соответствие одна или
несколько точек
ставится в соответствие одна или
несколько точек
![]() таких, что
таких, что
![]()
Заметим,
что «обратное» соответствие
![]() построить для всех с
возможно
не всегда. Поясним сказанное следующим
примером.
построить для всех с
возможно
не всегда. Поясним сказанное следующим
примером.
Пример3.
Функция
![]() удовлетворяет условиям теоремы Лагранжа
на отрезке
удовлетворяет условиям теоремы Лагранжа
на отрезке
![]() Однако для
Однако для
![]() не существует чисел
не существует чисел
![]() таких, что
таких, что
![]() ,
,
так как левая часть равенства положительна, а правая равна нулю.
