Важную роль при исследовании функции на выпуклость вверх (выпуклость вниз) играют точки, в которых происходит изменение направления выпуклости функции.
Определение
4. Точку
называют точкой
перегиба графика функции
,
если
непрерывна в точке
и слева и справа от этой точки кривая
имеет разные направления выпуклости.
В этом случае точку
называют точкой перегиба функции
(рис. 3, рис. 4).
Рис. 3 Рис. 4
Теорема 3.
Точка
,
для которой
или
не существует (причем
имеет смысл), является точкой перегиба,
только если
меняет свой знак при переходе через
.
Если
функция
непрерывна, но не дифференцируема на
отрезке
,
или трудно
отыскать корни уравнения
,
то задача определения направления
выпуклости функции значительно
усложняется. В этом случае бывает удобно
использовать различные эквивалентные
формы определений 1,2.
Теорема
4. Пусть
функция
непрерывна на отрезке
.
Тогда следующие условия эквивалентны:
1)
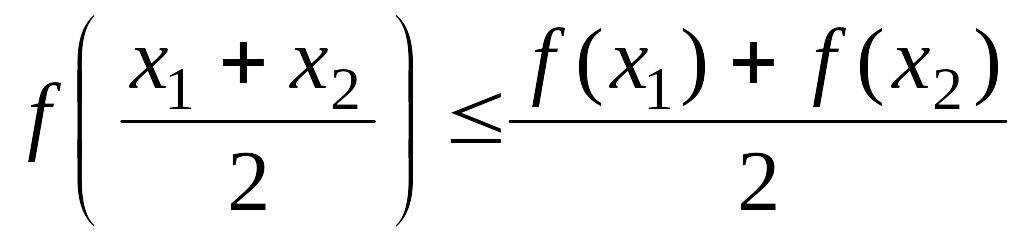для всех
2)
для каждого
выполнены
неравенства
для
всех
;
3)
выпукла вниз на отрезке
;
4)
для всех
и
.
Покажем,
что 3
4. Импликация 4
3 получается, если взять
.
Докажем импликацию 3
4, используя метод математической
индукции. Утверждение 4 верно для
по условию. Предположим, что оно выполнено
для
и докажем его для
.
Возьмем
.
Тогда
.
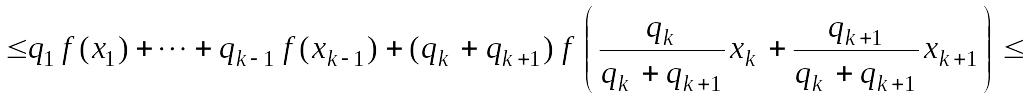
Упражнение
3.
Доказать:
1)
Решение. Доказывается аналогично .
Упражнение 4. Сформулировать теорему для выпуклых вверх функций, аналогичную теореме 4.
В этом разделе будут рассмотрены основные свойства выпуклых вниз (вверх) функций, заданных на отрезке .
1. Произведение выпуклой вниз функции на положительную (отрицательную) постоянную есть выпуклая вниз (выпуклая вверх) функция.
2. Сумма выпуклых вверх (вниз) функций является выпуклой вверх (вниз) функцией.
3.
Если
– однозначные взаимно обратные функции
и
,
то f
– выпукла вниз и возрастает
– выпукла вверх и возрастает; f
– выпукла
вниз и убывает
–
выпукла вниз и убывает; f
– выпукла вверх и убывает
–
выпукла вверх и убывает.
4.
Выпуклая вниз на отрезке
функция
,
отличная от постоянной, не достигает
наибольшего значения на интервале
.
Доказательство.
Предположим противное. Тогда существует
точка
такая, что
.
Так как функция отлична от постоянной,
то найдутся точки
такие, что
Причем
хотя бы одно из неравенств – строгое.
Выберем положительные числа
таким
образом, чтобы было выполнено равенство
и
Тогда
что
противоречит выпуклости вниз функции
.
5.
Пусть функция
непрерывна, выпукла вниз на отрезке
и
существуют положительные числа
и
для которых выполняется равенство
Тогда
равенство
выполняется для всех точек
.
Доказательство.
Пусть
– уравнение прямой, проходящей через
две точки
.
Тогда функция
выпукла вниз как сумма двух выпуклых вниз функций и
Представим
произвольную точку
в виде
и получим
.
Покажем,
что
.
Действительно, если предположить, что
для некоторого
,
то
Следовательно,
является точкой максимума функции
,
что противоречит свойству 4, так как
.
Таким образом,
.
Это означает, что график функции
совпадает с хордой
.
Следовательно,
– линейная функция, то есть,
для всех
и
.
Замечание 1. Показать, что – линейная на функция тогда и только тогда, когда для всех и .
Замечание
2. При
исследовании выпуклых вверх (выпуклых
вниз) на
функций бывает удобно рассмотреть
функцию
,
построенную в доказательстве свойства
5, так как эта функция имеет то же
направление выпуклости, что и исходная,
и
,
что делает функцию
удобной для изучения.
Определение выпуклой вверх (выпуклой вниз) функции является своеобразным генератором для получения различных неравенств. Все приводимые ниже неравенства получаются из теоремы 4:
а)
Так как
то
– выпуклая вниз функция. Следовательно,
для
.
В частности,
для любого
;
б) функция
выпукла вверх на
.
Поэтому
для
.
В частности,
для любого
;
в) функция
выпукла вниз на
.
Поэтому
для
> 0 и
.
Упражнение
4. Доказать, что если
функции
и
являются взаимно обратными функциями
(на соответствующих промежутках) и
функция
выпуклая вниз и возрастает, то функция
выпуклая
вверх.
Решение.
Пусть
,
где
и
− любые точки из промежутка, на ко−
тором функция
выпуклая вниз и возрастает. Так как
и
− обратные функции то
,
,
,
.
Поскольку функция выпуклая вниз, то
.
Так как по свойству обратных функций функция является воз− растающей, то
,
что и доказывает выпуклость вверх функции .