Примеры решения задач

Пример 3. Доказать, что если функция непрерывна на и любые точки из этого интервала, то найдется число такое, что

и .

Решение. Не ограничивая общности, будем считать, что

.

Тогда функция

непрерывна и удовлетворяет условиям

Если одно из неравенств обращается в равенство, то можем взять где или .

Если и , то по теореме 7 найдется число между и такое, что .

Из равенства получаем

.

Пример 4. Найти

Решение.

.

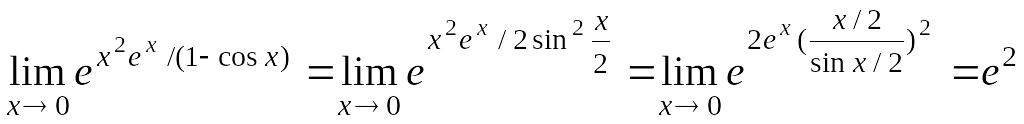Пример 5. Исследовать на непрерывность функции:

1) 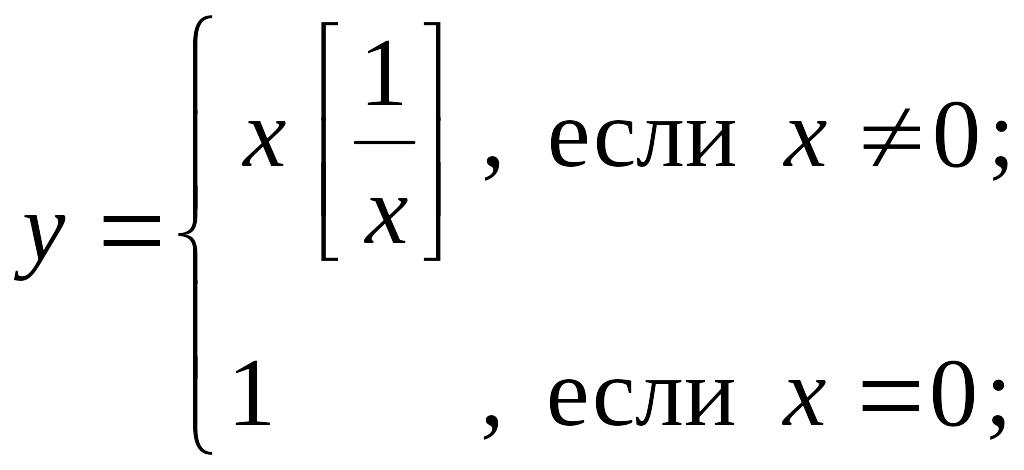2) .

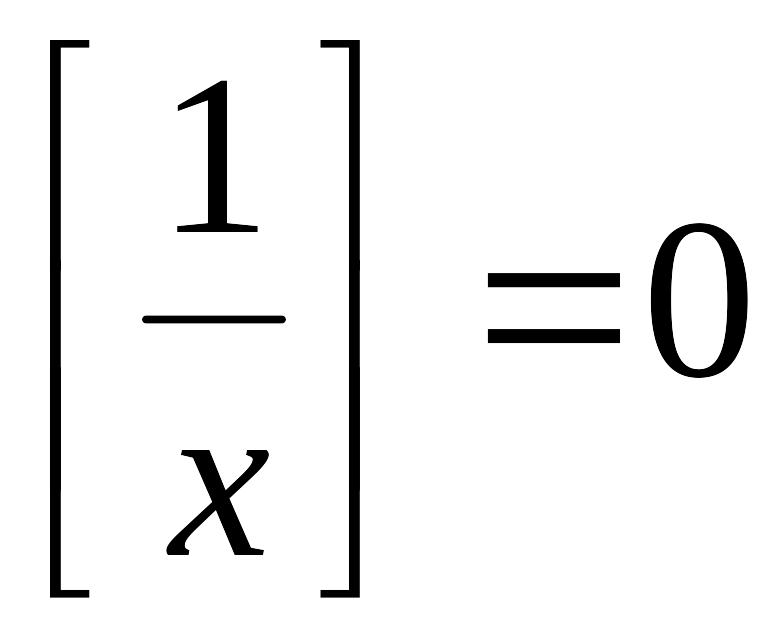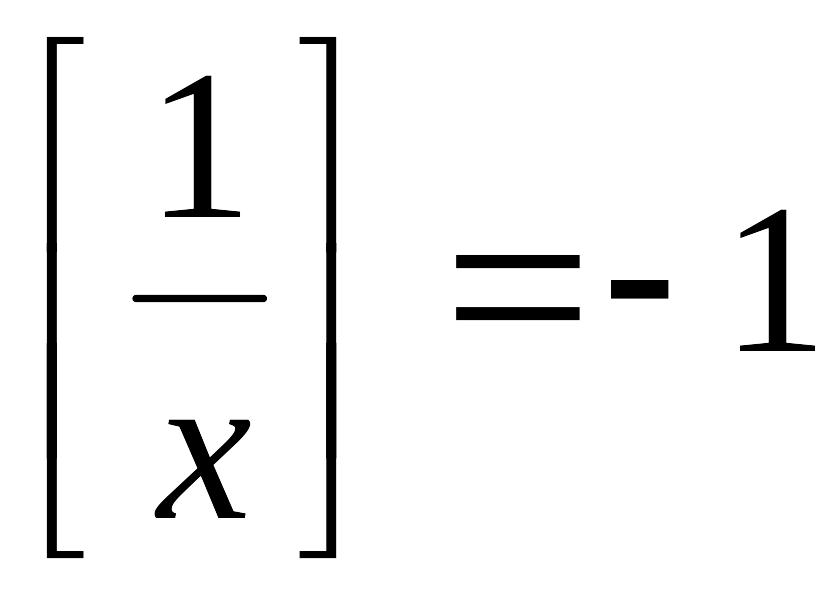Решение. 1а) если , то и . Следовательно, . Если , то и .

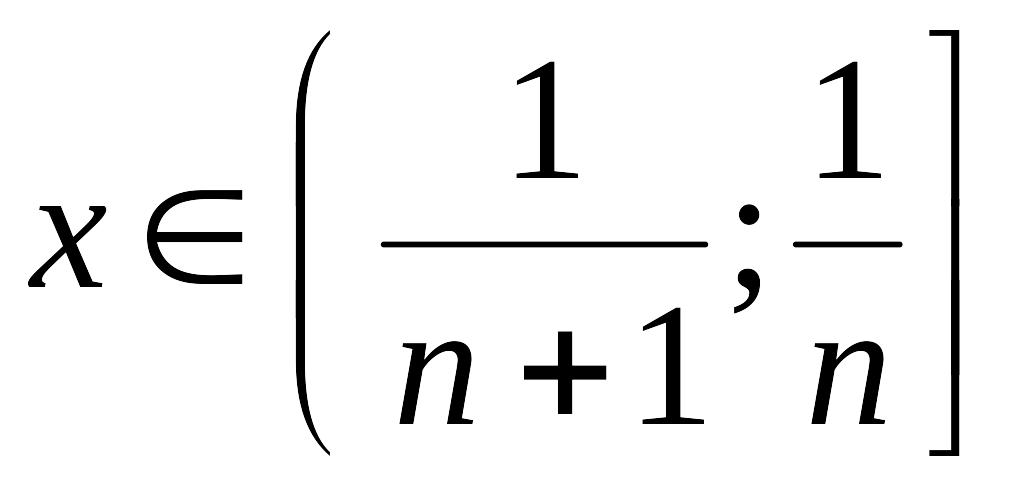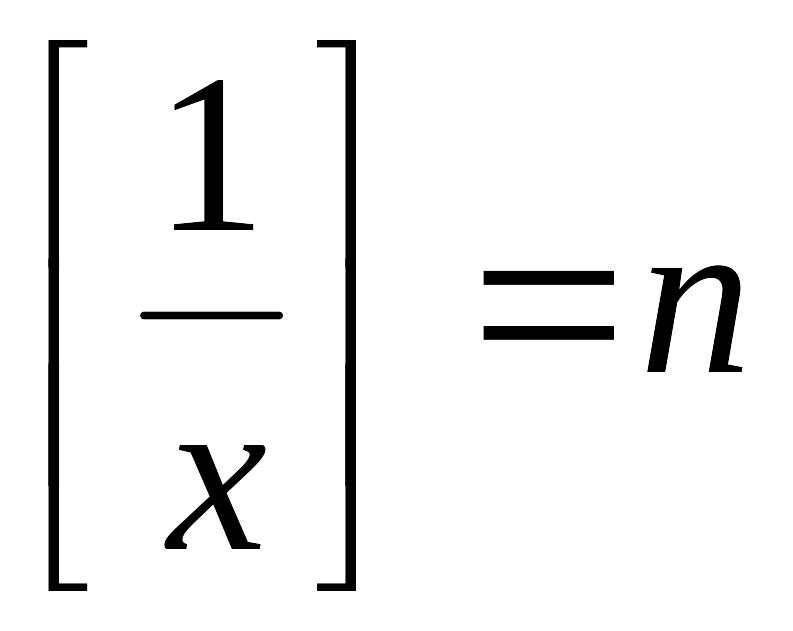1б) пусть , где . Тогда и .

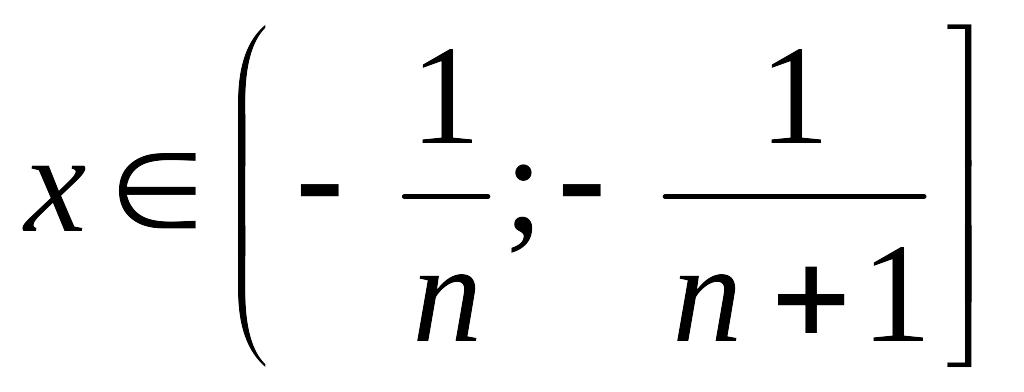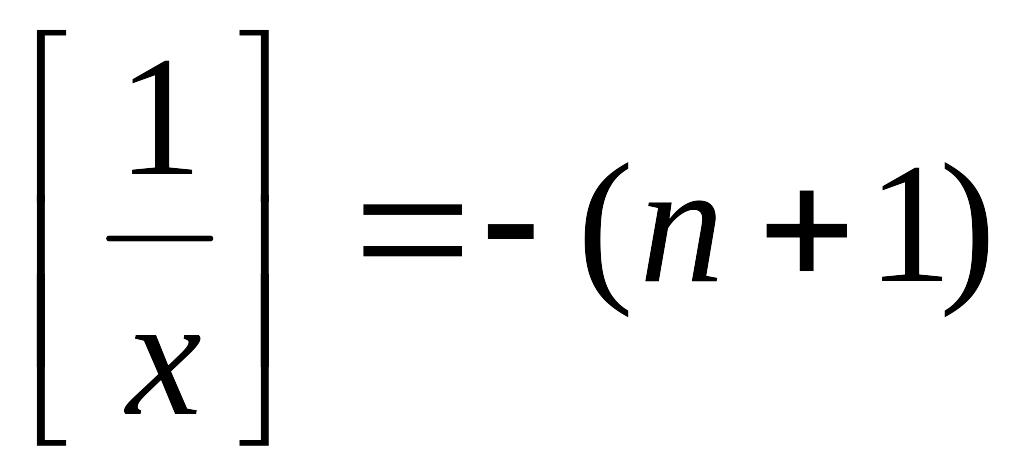1в) пусть , где . Тогда и .

Таким образом, функция непрерывна на каждом множестве , 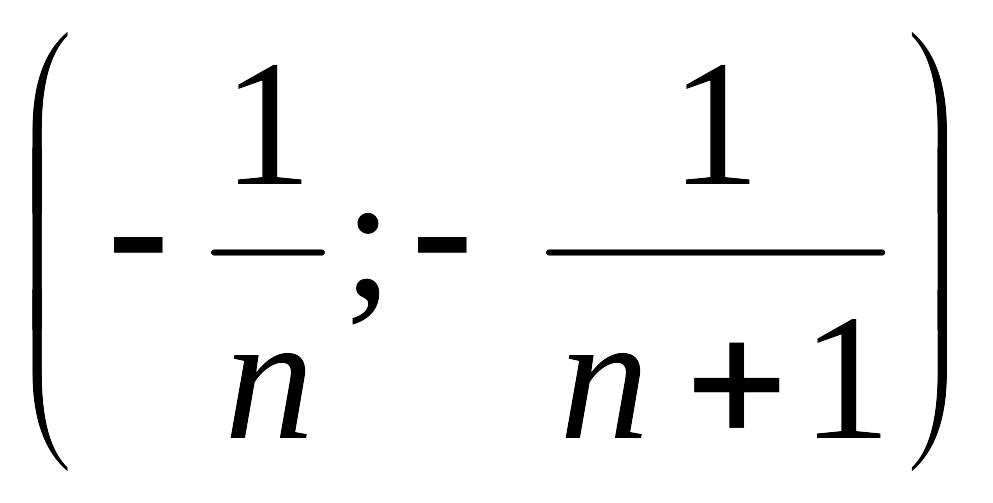и 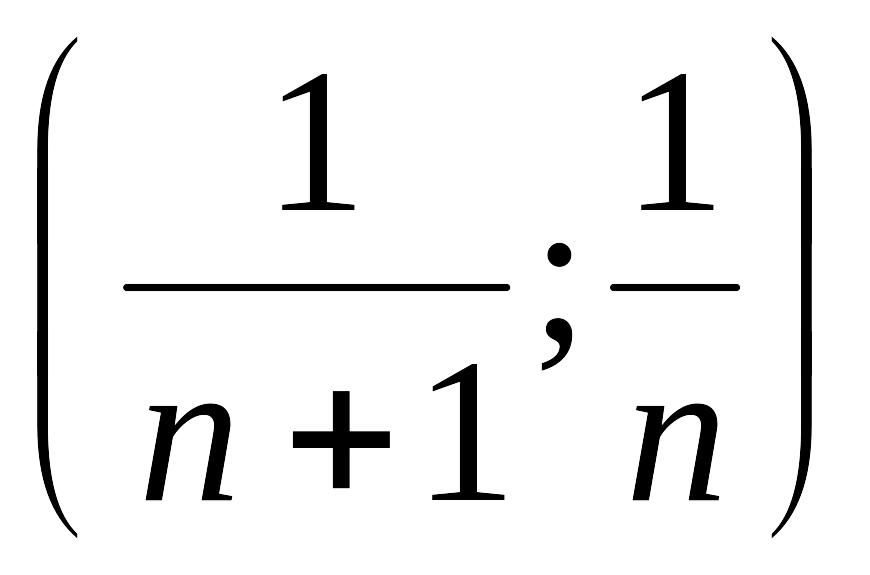, где . Исследуем функцию на непрерывность в точках :

.

.

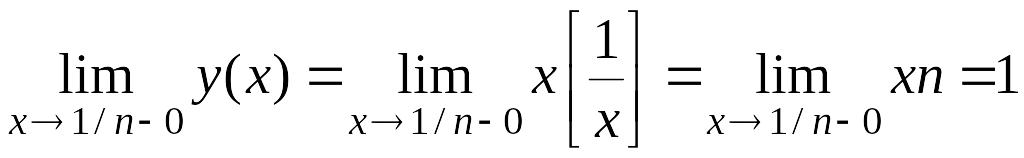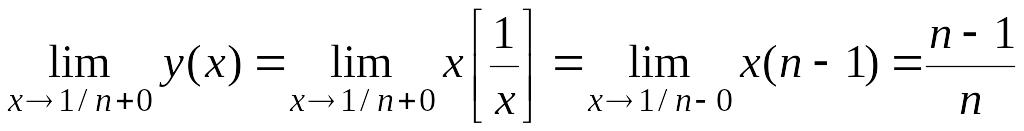Следовательно,

и точки , являются точками разрыва функции . Аналогично доказывается, что функция имеет разрыв в точках . Покажем, что непрерывна в точке . Так как для всех , то для

Переходя к пределу при , получаем . Аналогично .

2) Рассмотрим следующие случаи:

а) . Тогда и для выполнено неравенство . Следовательно,

Таким образом,

Отсюда получаем, что

б) и .

в) . В этом случае и

Из а, б, в следует, что непрерывна всюду.

Пример 6. Вычислить .

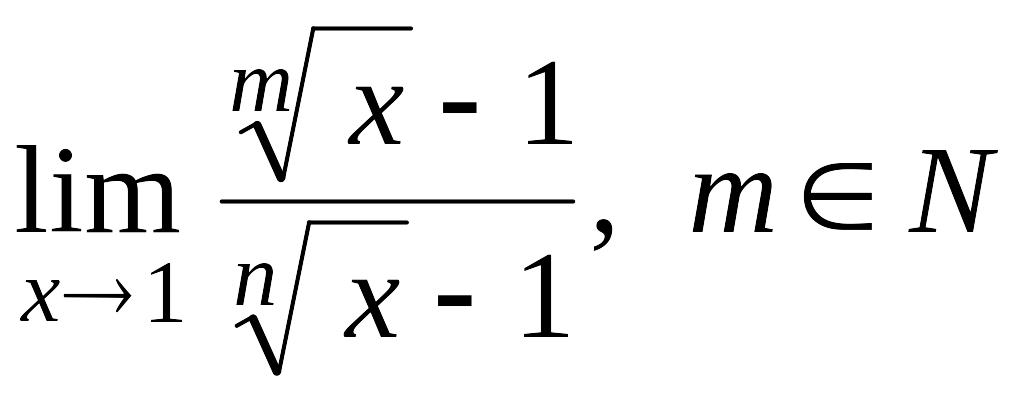Решение. Сделаем замену . Тогда при и

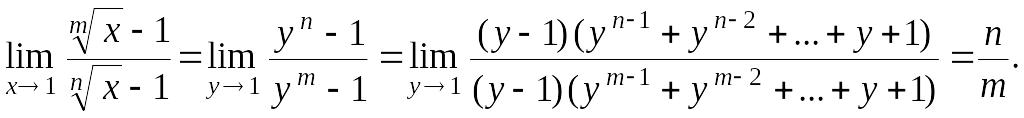
Пример 7. Пусть не является непрерывной на отрезке . Что можно сказать о непрерывности функций ?

Решение. Функция может быть как непрерывной, так и разрывной функцией в зависимости от выбора функции . Приведем соответствующие примеры.

1. Пусть

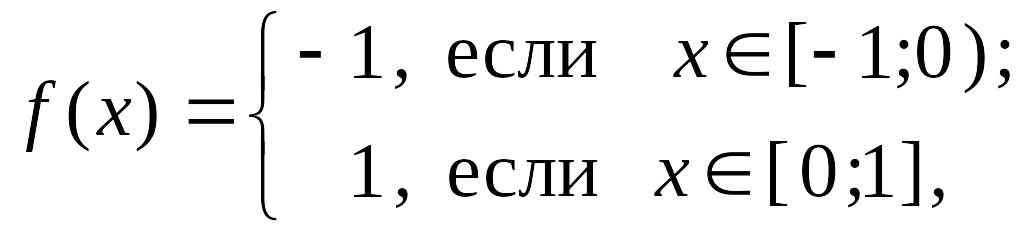
тогда имеет разрыв в точке , а непрерывная на функция.

2. Пусть

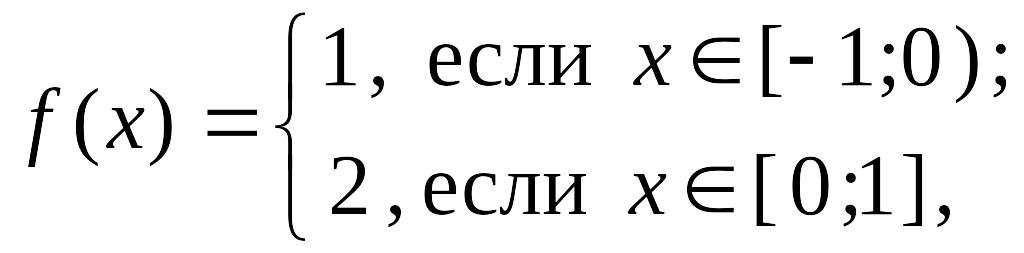
тогда обе функции и имеют разрыв в точке .

Пример 8. Доказать, что если функция непрерывна на отрезке и имеет обратную функцию, то она монотонна на этом отрезке.

Решение. Из существования обратной функции следует, что в разных точках отрезка принимает различные значения. Следовательно, . Будем считать, что . Если предположить, что не является монотонно возрастающей на , то найдутся точки такие, что

Рассмотрим следующие возможные случаи.

1. .

По теореме 7 части 2 на интервале найдется точка  такая, что , что противоречит существованию обратной функции.

2. .

В силу сделанного предположения и, следовательно, найдется такая, что и , так как . Получили противоречие аналогично пункту 1.

3. .

Этот случай рассматривается аналогично пункту 2. Таким образом, сделанное нами предположение неверно и монотонна на .

Пример 9. Доказать, что если монотонна на и при-нимает все значения между и , то эта функция непре-рывна на .

Решение. Предположим, что монотонно возрастает на и имеет разрыв в точке .

Обозначим . Так как возрастает на , то и выполнены условия

для всех ,

для всех .

Это означает, что не принимает значений из интервала , вложенного в 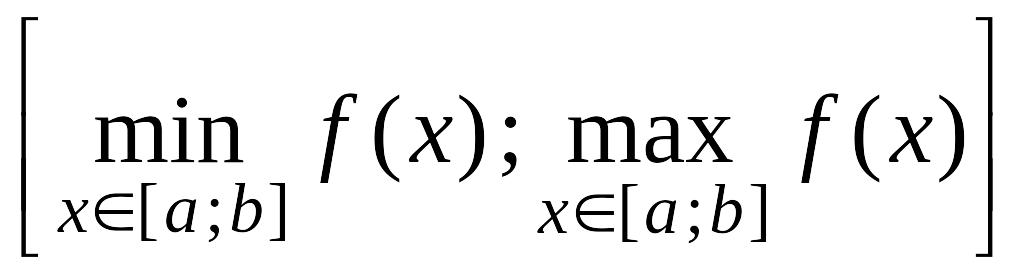. Получили противоречие. Аналогично доказывается, что непрерывна в концах отрезка .

Пример 10. Функция непрерывна при и . Доказать, что ограничена на .

Решение. Предположим, что не ограничена на . Тогда найдется последовательность такая, что выполнено равенство . Так как конечен, то выбранная по-следовательность ограничена, то есть . По теореме 7 ограничена на и, следовательно, найдется такое, что . В частности, . Получили противоречие.