Упражнение 14. Найти

Решение.

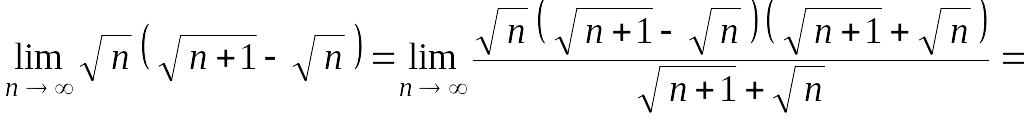
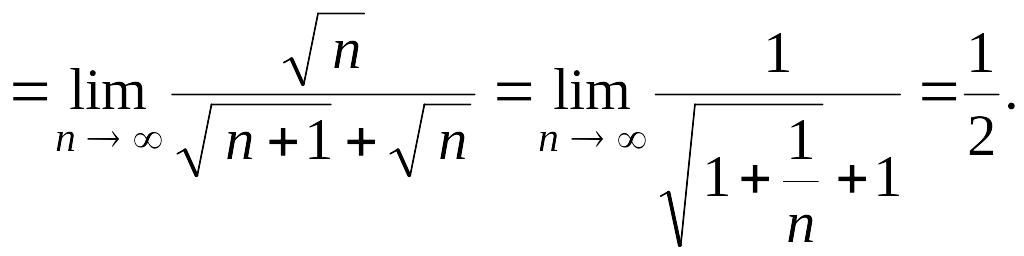
Более универсальный метод вычисления рассмотренных выше пределов дает применение правила Лопиталя. Еще один метод вычисления пределов последовательностей, выходящий за рамки теории последовательностей, связан с использованием интегральных сумм Римана. Оба эти метода будут рассмотрены ниже.

Примеры решения задач

Рассмотрим нестандартные приемы вычисления пределов последовательностей на конкретных примерах.

Пример 1. Вычислить , если

, для .

Решение. Заметим, что для любого справедливы равенства

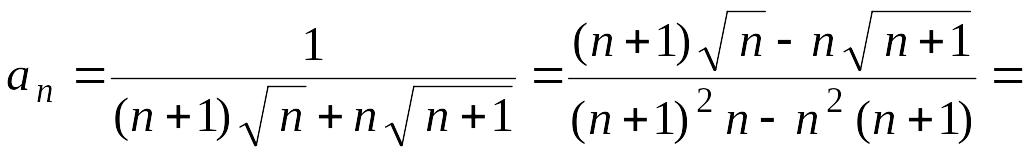
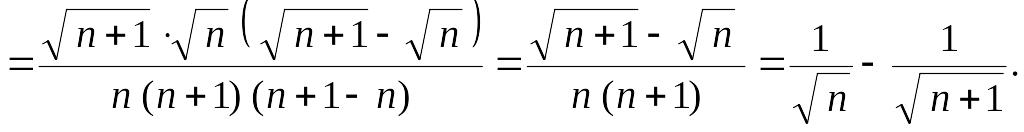
Отсюда

.

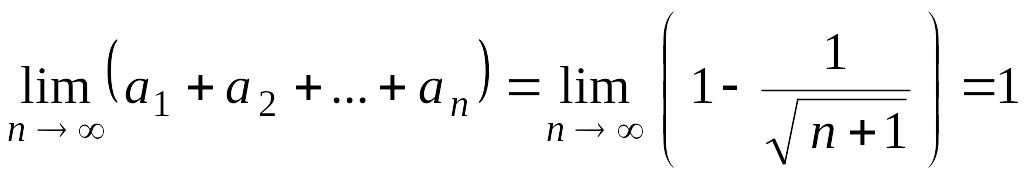Пример 2. Пусть , . Найти .

Решение. Запишем в виде

Непосредственными вычислениями проверяется, что 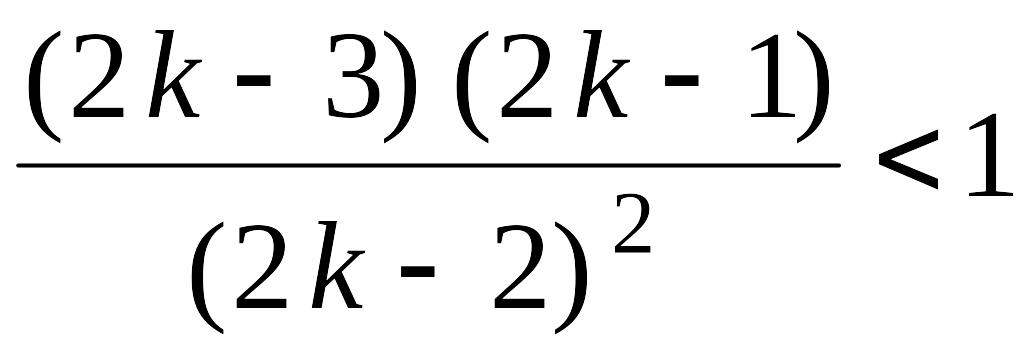для всех . Отсюда вытекает оценка Отсюда и из теоремы 4 получаем равенство . Это означает, что = 0.

Пример 3. Пусть – все положительные корни уравнения , расположенные в порядке возрастания. Вычислить .

Решение. Так как функция на каждом полуинтервале 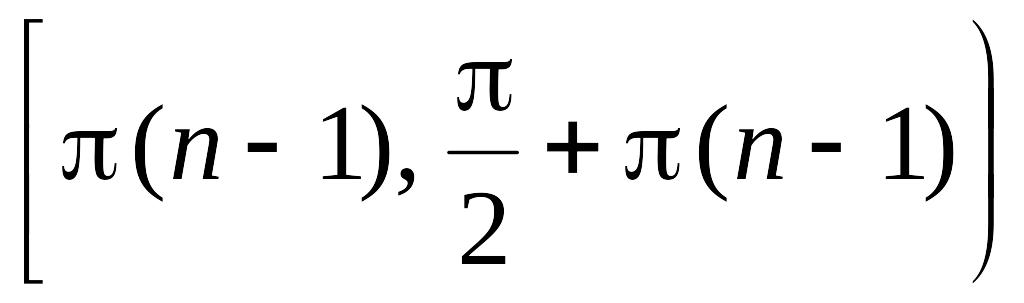возрастает от 0 до , то 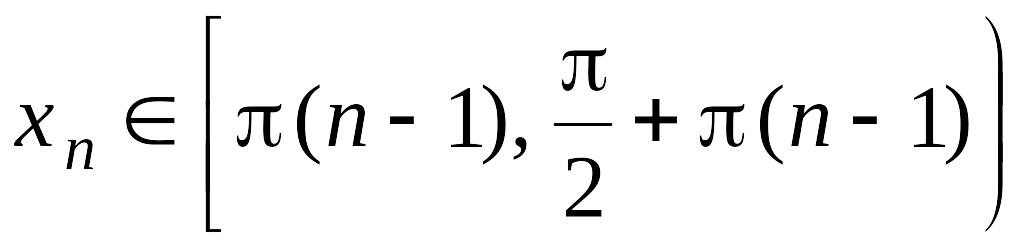, . Отсюда следует, что

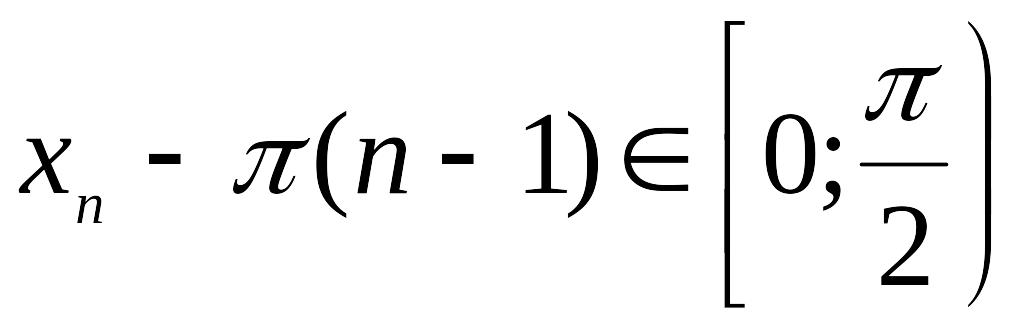Так как и для всех , то при . Таким образом,

Пример 4. Числовая последовательность задана соотношением . Определить, при каких значениях a и b последовательность сходится, и вычислить ее предел.

Решение. Предположим, что данная последовательность имеет предел, равный А. В этом случае

Таким образом, и

Из неравенства следует, что последовательность возрастает. Так как ее предел равен а, то для всех должно быть выполнено неравенство

Для того чтобы найти условия на , вытекающие из последнего неравенства, рассмотрим функцию и найдем решение неравенства :

Отсюда . Это означает, что члены удовлетворяют условию: для всех . В частности, Таким образом, условие является необходимым для сходимости . Покажем, что оно является и достаточным.

Итак, пусть . Используя метод математической индукции, покажем, что условие выполняется для всех . Для оно выполнено в силу равенства . Предположим, что двойное неравенство выполнено для некоторого . Покажем, что в этом случае выполняется неравенство .

С другой стороны, так как , то и

Из полученных неравенств следует, что и . Применяя метод математической индукции, получаем, что и для всех . По теореме 2 последовательность сходится и, как было доказано выше,

Таким образом,

сходится и

Пример 5. Даны три числа По этим числам строятся средние арифметические

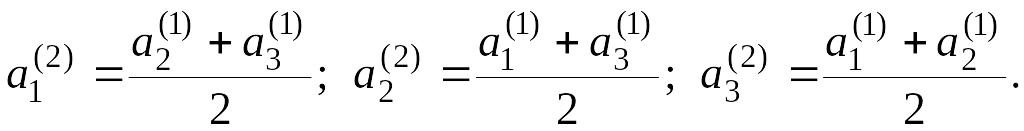
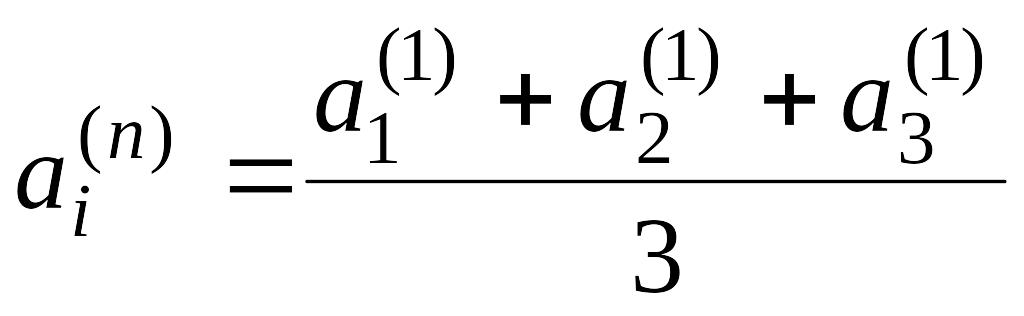Затем по тому же правилу строятся и т. д. Доказать, что для

Решение. Пусть попарно различные числа из множества . Тогда

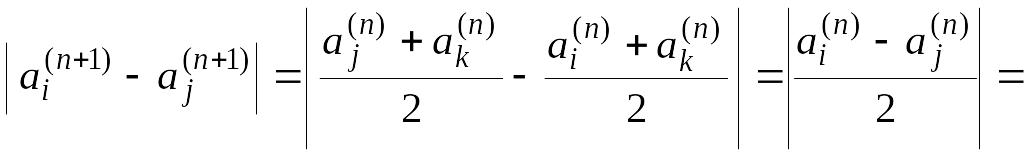
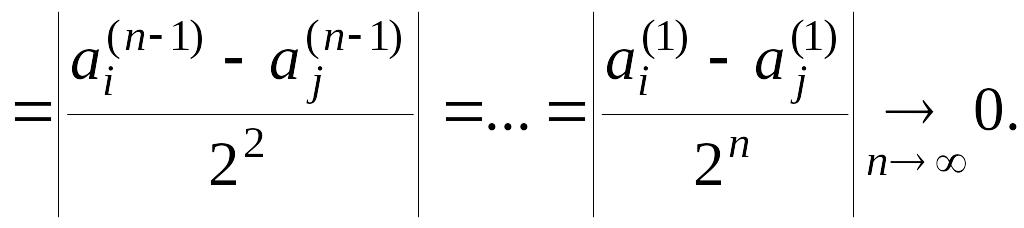
Обозначим Как мы видели выше, для Покажем теперь, что сумма не зависит от номера . Действительно,

.

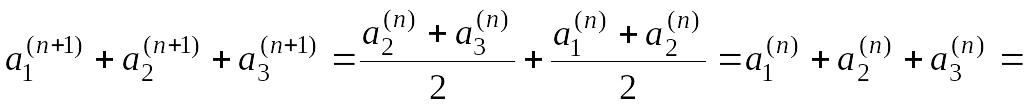
Обозначим

Из равенства

получаем

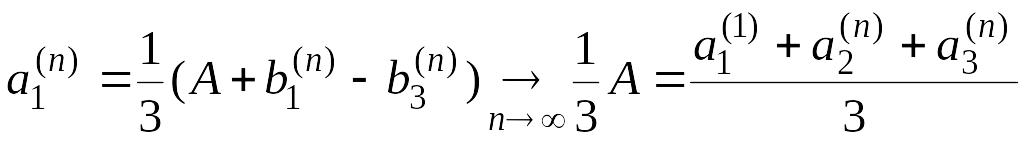
аналогично

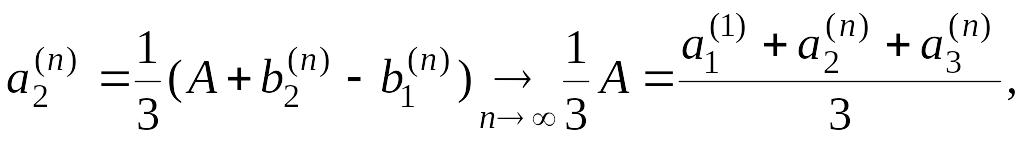
Пример 6. Найти предел 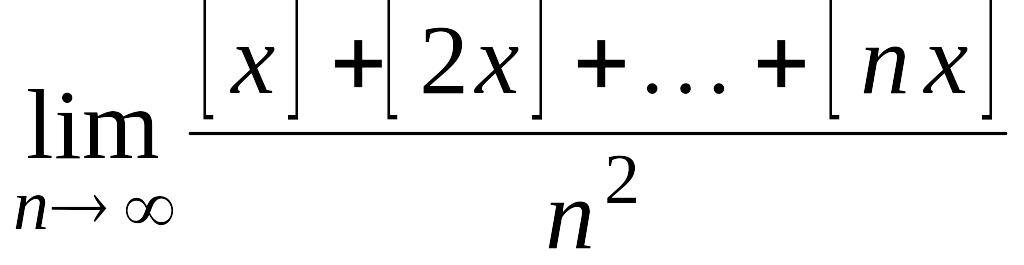, где − произвольное число, – его целая часть, то есть наибольшее целое число, не превосходящее х.

Решение. Из определения целой части числа следует, что для всех . Тогда

,

,

.

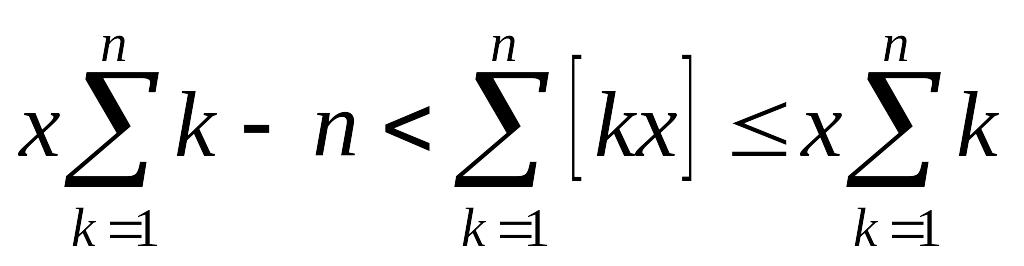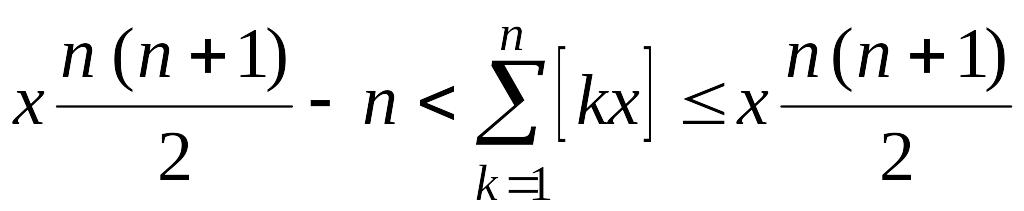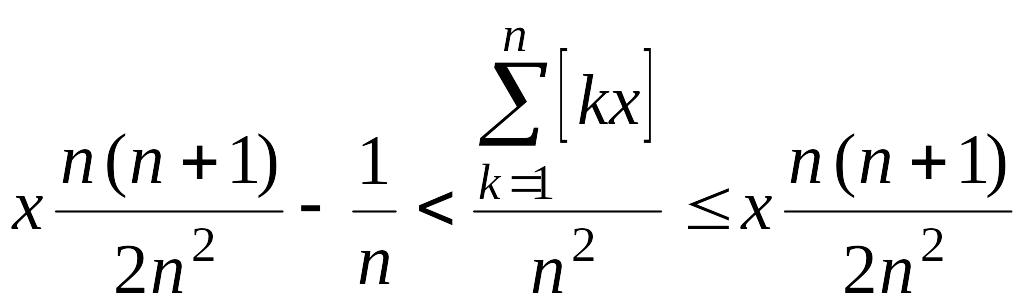Переходя к пределу при , получаем

.

Таким образом,

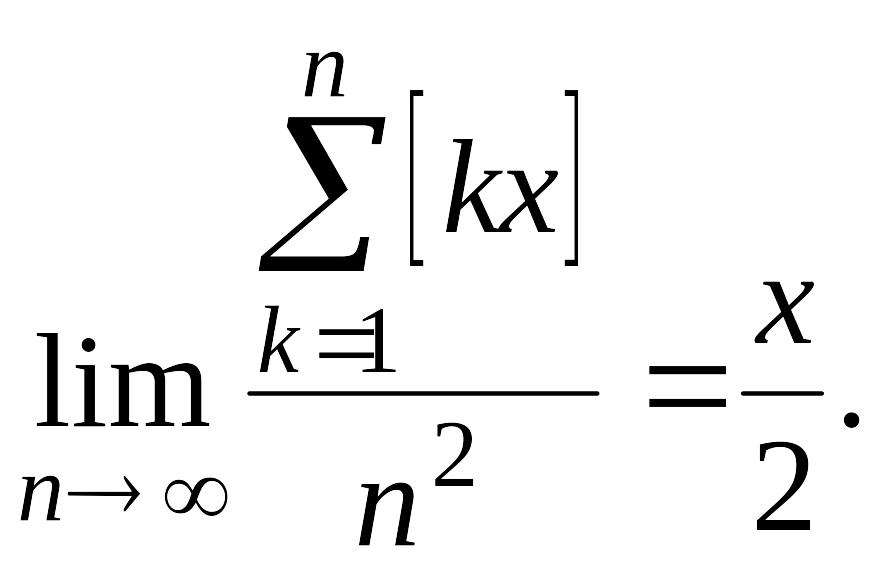
При рассмотрении следующего примера предполагается, что читатель знаком с основами теории рядов.

Пример 7. Найти

Решение.

= =

=

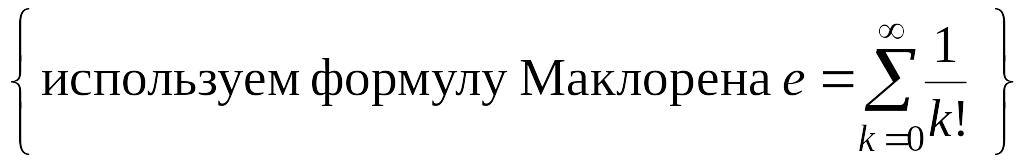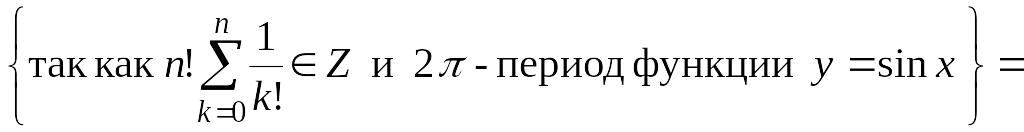
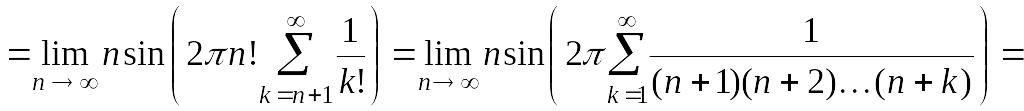
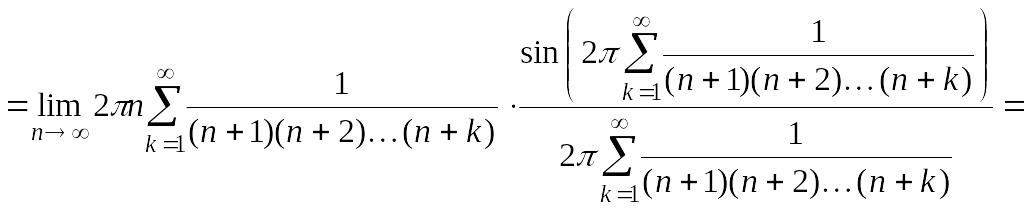
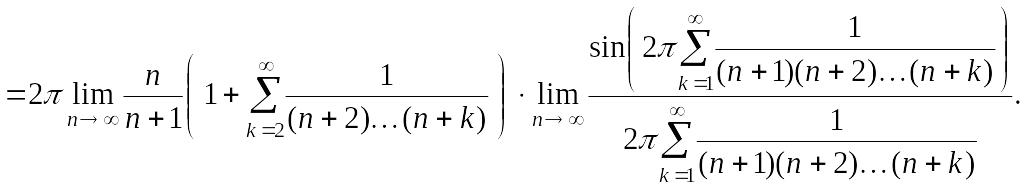Так как ряд 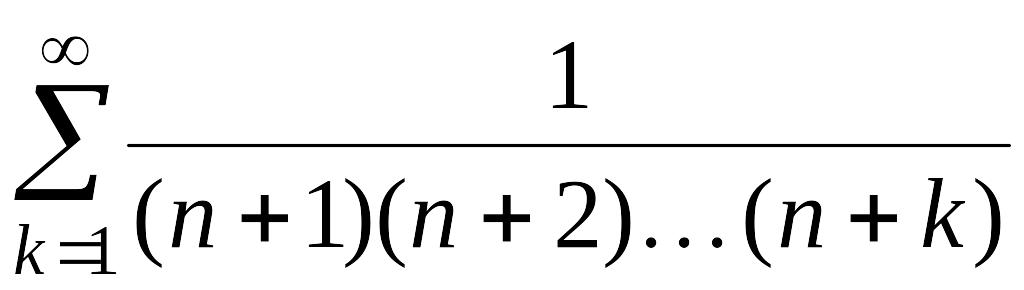сходится, то его остаточный член стремится к 0, следовательно, 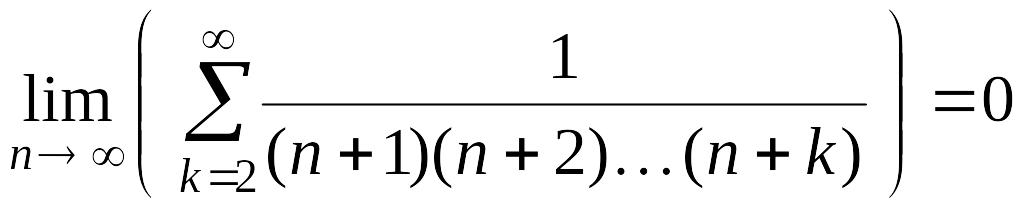. Второй предел равен 1 в силу соотношения 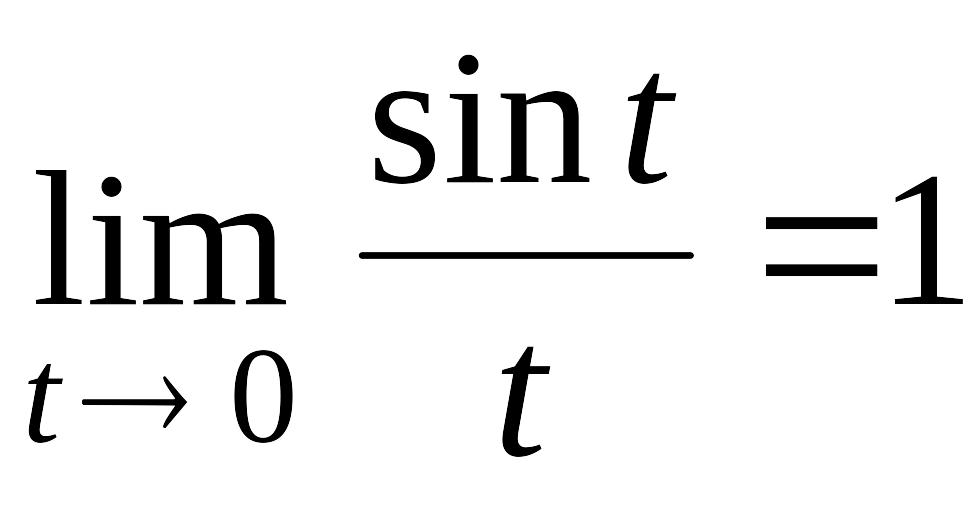. Таким образом,

Пример 8. Пусть – последовательность с ограниченным изменением, то есть существует такое, что

для всех .

Доказать, что последовательность сходится.

Решение. Рассмотрим последовательность

.

Так как возрастает и ограничена сверху константой , то последовательность сходится. Применив к ней критерий Коши, получим

,

Из неравенства треугольника следует, что

.

Таким образом,

,

то есть удовлетворяет условию критерия Коши и, значит, сходится к конечному пределу.