Задачи для самостоятельного решения
Доказать равенства:
а)
;
б)
;
в)
.
2. Доказать неравенства:
а)
б)
– числа
одного и того же знака, большие чем –1;
в)
;
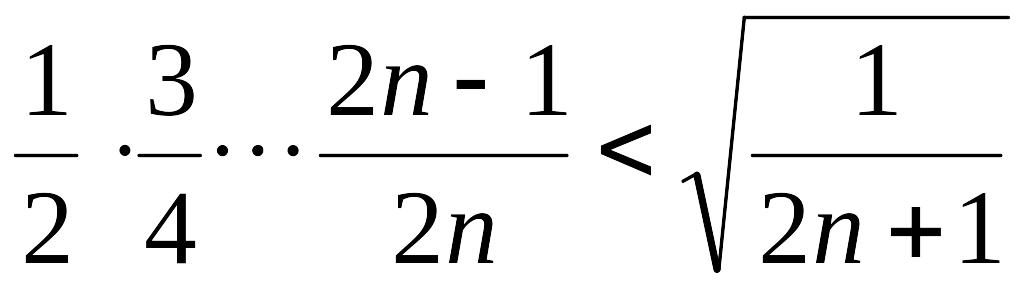г)
;
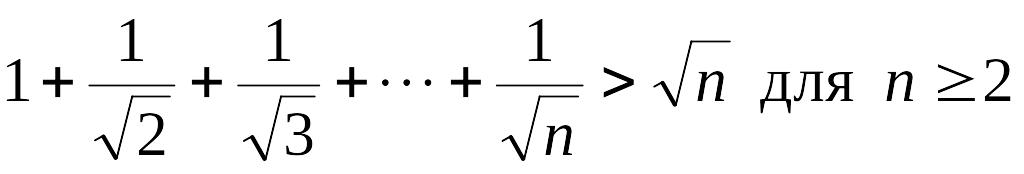д)
.
2.2. Пределы последовательностей
Определение
1. Число
называется пределом
последовательности
если для каждого
существует
такой номер
N,
что для всех
выполняется
неравенство
.
Это
обозначают так:
.
При помощи символов математической логики это определение можно записать в виде
Аналогично можно записать следующие определения:
,
,
.
Геометрически
факт
означает, что для любого
вне интервала (
)
находится не более конечного числа
членов последовательности
;
факт
означает, что найдется интервал
,
вне которого находится бесконечно много
членов
.
Последовательности, имеющие конечный предел, называются сходящимися, а остальные – расходящимися.
Критерий
Коши сходимости последовательности.
Существование у последовательности
конечного предела эквивалентно выполнению
условия
Основные свойства пределов последовательностей заключены в следующей теореме.
Теорема
1. Если существуют конечные
пределы
то
1)
2)
3)
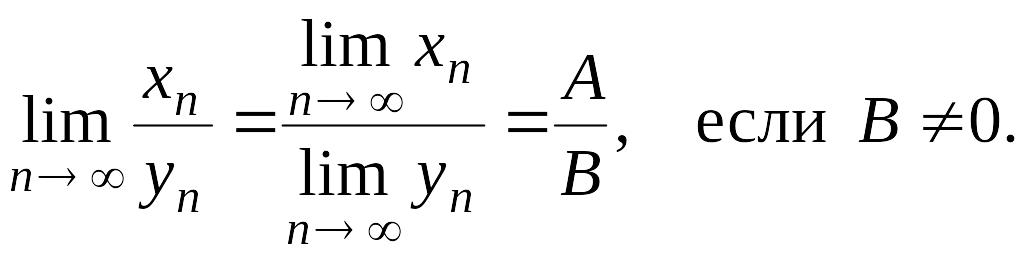
Несколько
более сложным и интересным является
исследование сходимости последовательностей
,
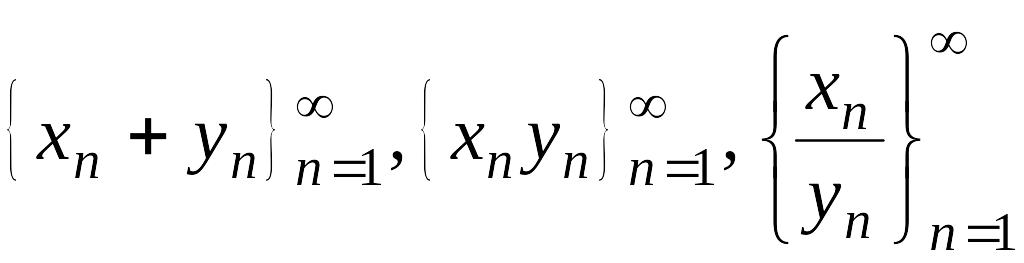в случае когда один или оба предела
не существуют или равны бесконечности.
Утверждение
1. Пусть последовательность
сходится, а последовательность
расходится, тогда
1)
последовательность
расходится;
2)
последовательность
:
а)
расходится, если
б)
может расходиться, сходиться к
бесконечности или конечному пределу,
если
Доказательство.
1. Предположим, что
сходится, тогда
существует и конечен. Противоречие.
2. Доказательство 2а аналогично доказательству 1.
Приведем примеры, соответствующие каждой из возможностей, сформулированных в условии 2б.
Если
Если
Если
для
нечетных
,
то
для четных
и
для нечетных
.
Таким образом,
не существует.
Определение 2. Последовательность
называется ограниченной
сверху (снизу), если существует
такое, что
для всех
.
Последовательность
называется ограниченной,
если она ограничена снизу и сверху.
Замечание.
Пункт 2б утверждения 1 может быть
частично уточнен следующим образом:
если
и последовательность
ограничена, то
Упражнение 1.
Привести примеры расходящихся
последовательностей
,
таких, что
-
1)
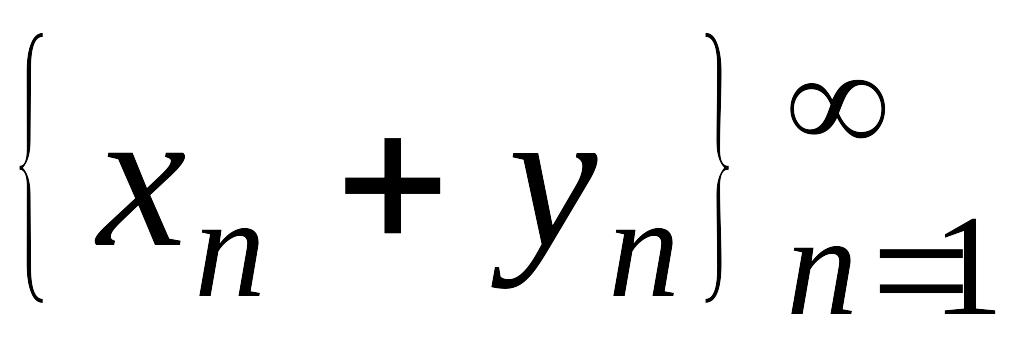сходится;2) расходится;
3)
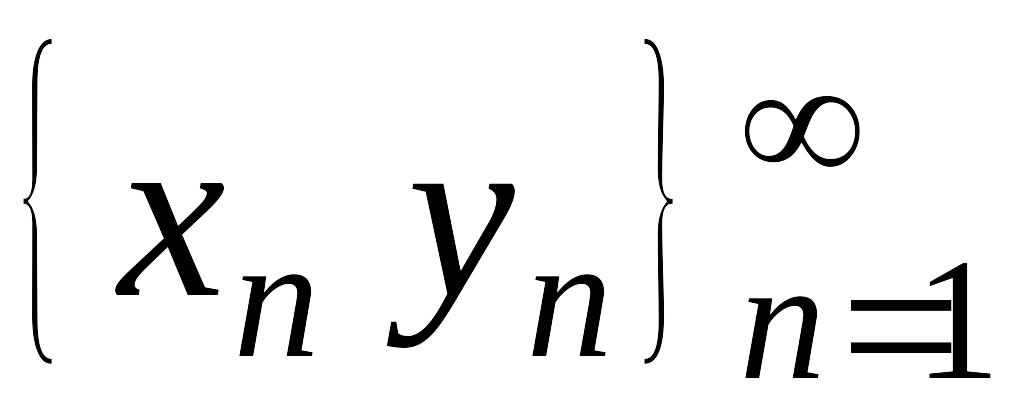сходится;4) расходится.
Приведем значения пределов некоторых, часто встречающихся на практике последовательностей :
-
;
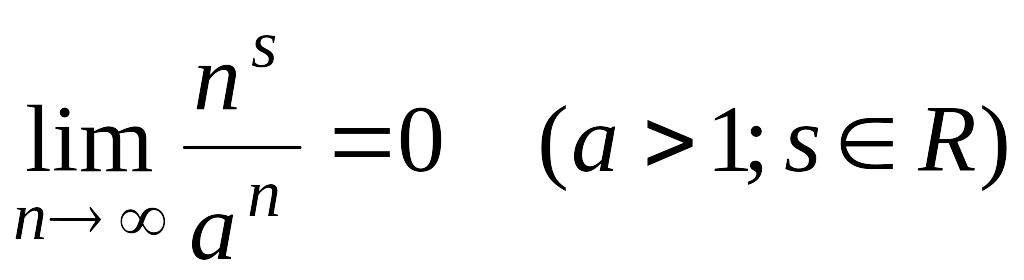3)
;
;
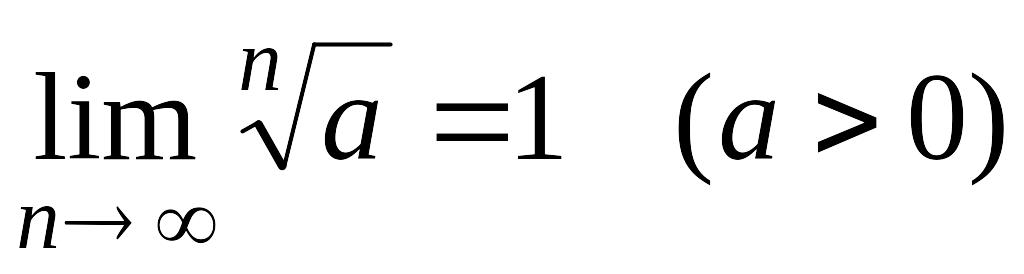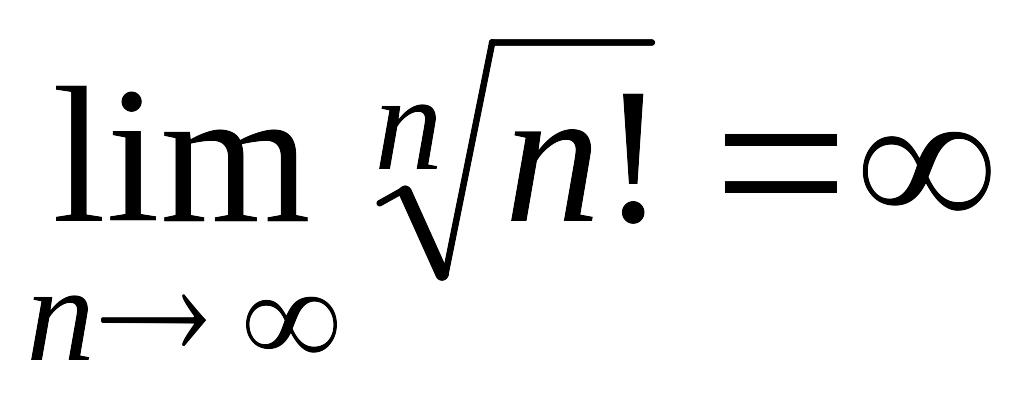7)
;
;
;
;
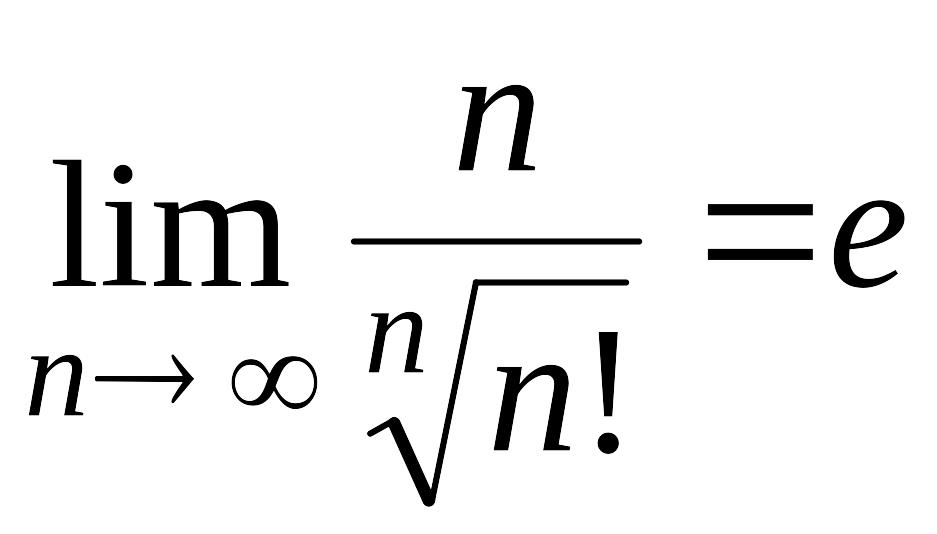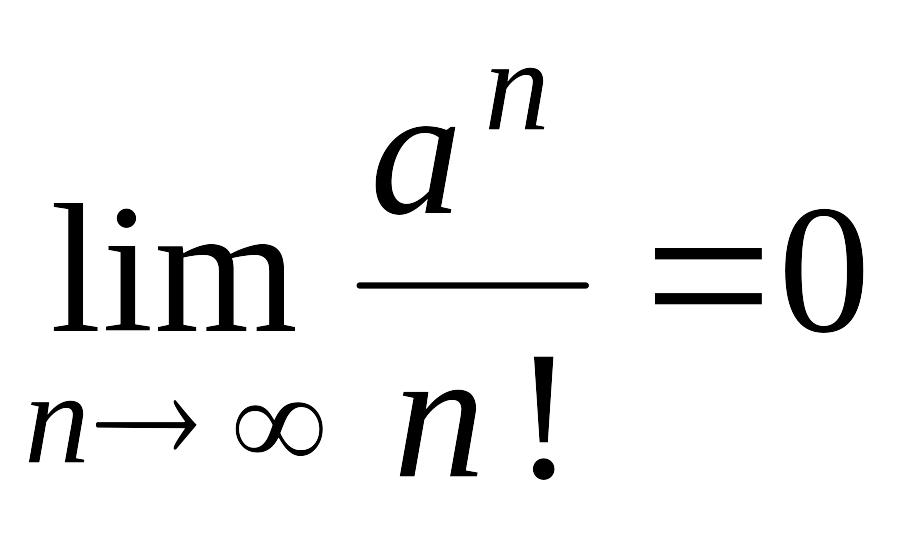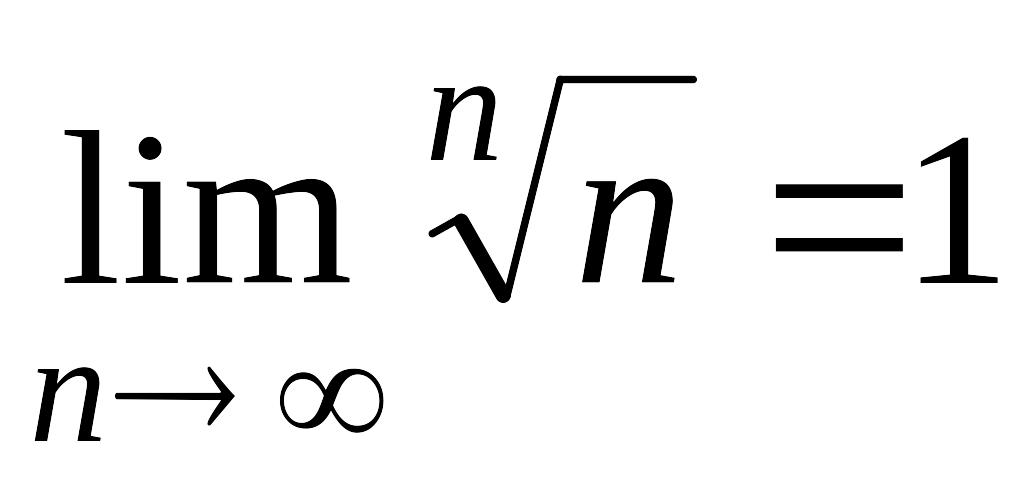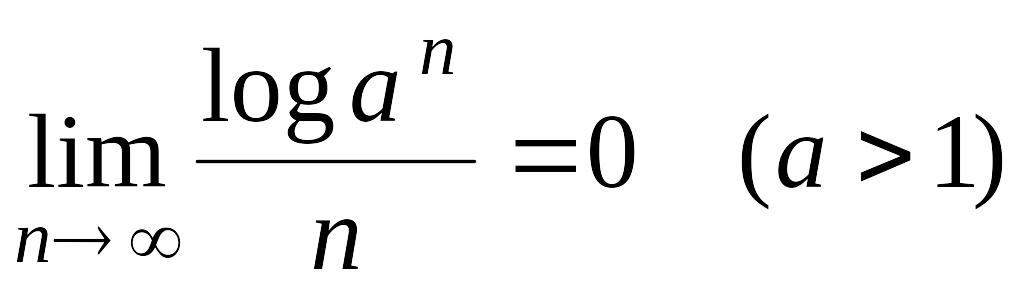8)
.
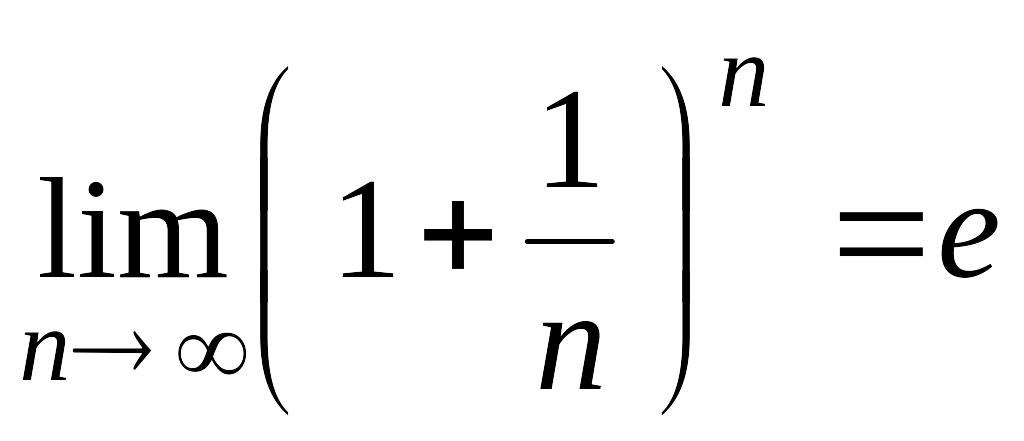Различные подходы к доказательству сформулированных результатов будут даны в этом и последующих разделах.
Во многих случаях доказательство существования у последователь-ности конечного предела основывается на использовании следующей теоремы.
Теорема 2. Монотонно возрастающая, ограниченная сверху последовательность имеет конечный предел. Монотонно убывающая, ограниченная снизу последовательность имеет конечный предел.
Эта теорема часто используется для вычисления пределов рекуррентно заданных последовательностей. Проиллюстрируем сказанное следующим упражнением.
Упражнение
2. Последовательность
такова, что
,
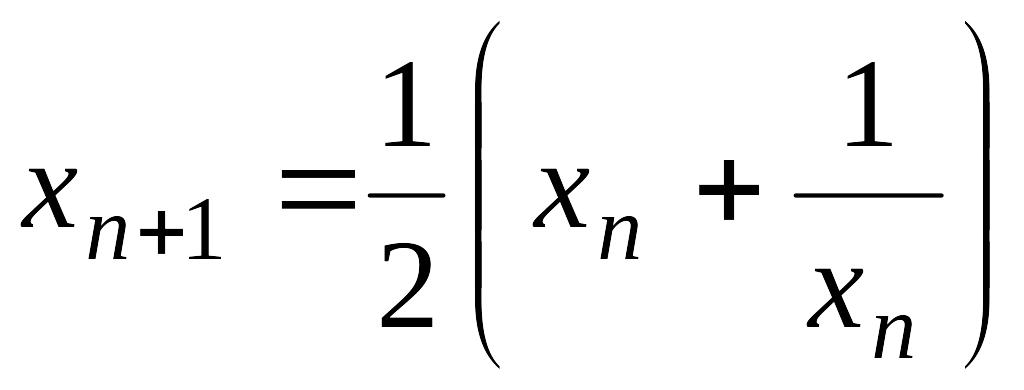при
.
Доказать, что существует
,
и найти этот предел.
Решение.
Во-первых, покажем, что
для всех
:
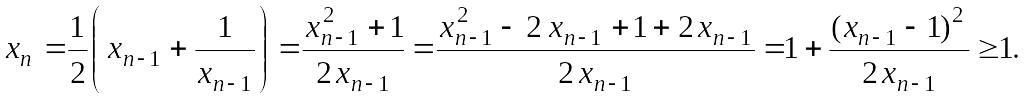
Используя полученную оценку, установим, что последовательность монотонно убывает:
.
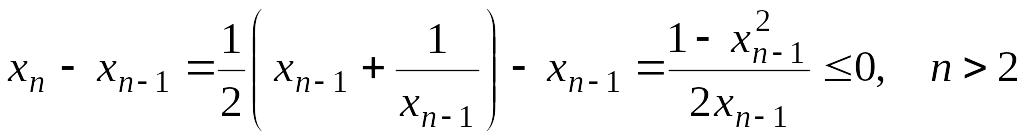Таким
образом, выполнены условия теоремы 2 и,
следовательно, существует предел
последовательности
Обозначим его А. Тогда
и
,
,
.
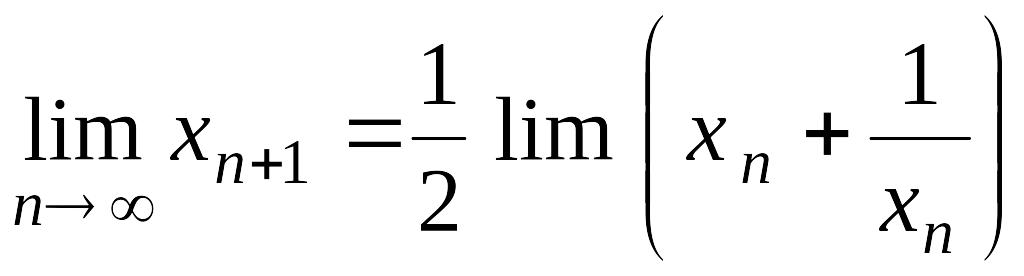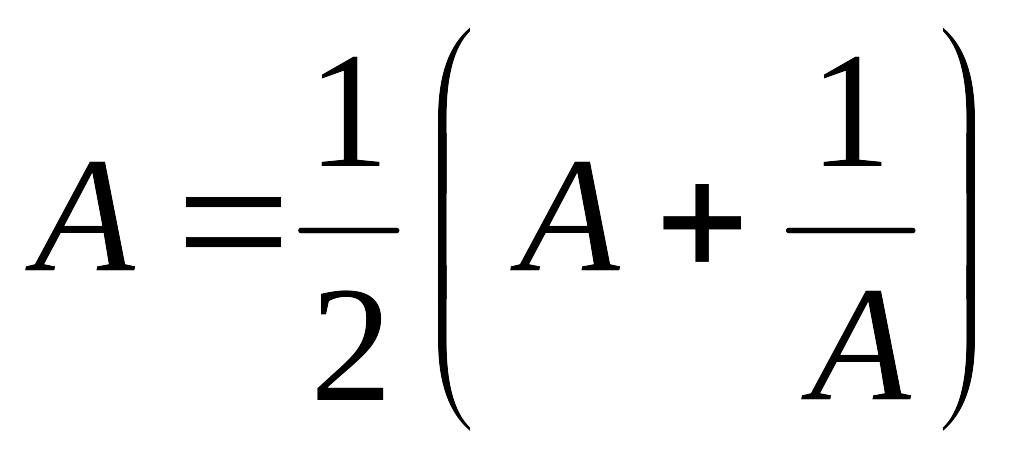Так
как все
то
.
Упражнение
3. Для
вычислить предел последовательности
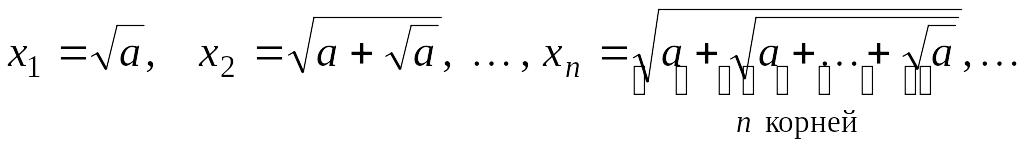
При
вычислении пределов последовательностей,
заданных рекуррентной формулой
,
бывает полезно использовать следующее
соображение. Пусть
и
– корни уравнения
.
Тогда
,
если
;
,
если
.
Коэффициенты
и
определяются по двум первым членам
последовательности, заданным в условии
задачи. Представленные формулы можно
доказывать в каждом конкретном случае
методом математической индукции. Общий
подход к доказательству этих равенств
достаточно труден и потому выходит за
рамки нашего изложения.
Упражнение
4.
Пусть дана рекуррентная последовательность:
для
.
Вычислить предел
.
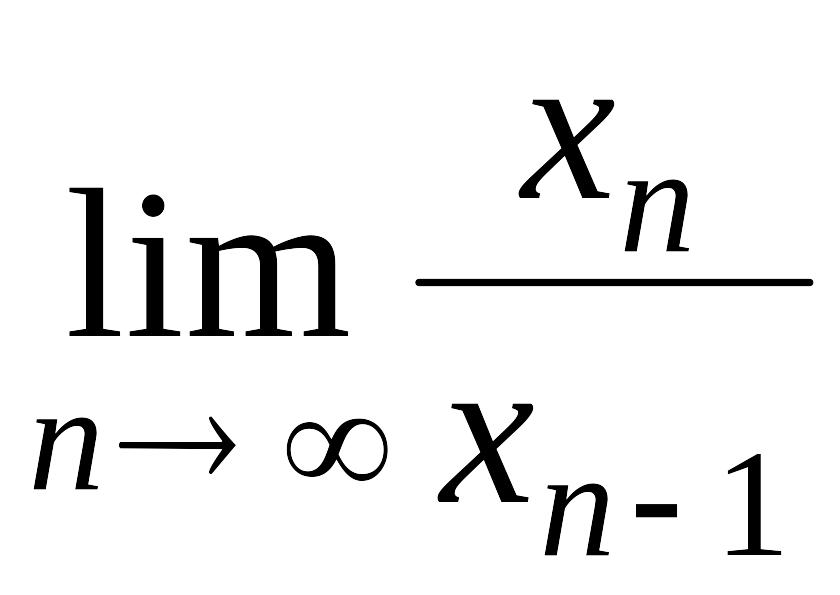Решение. Покажем, что
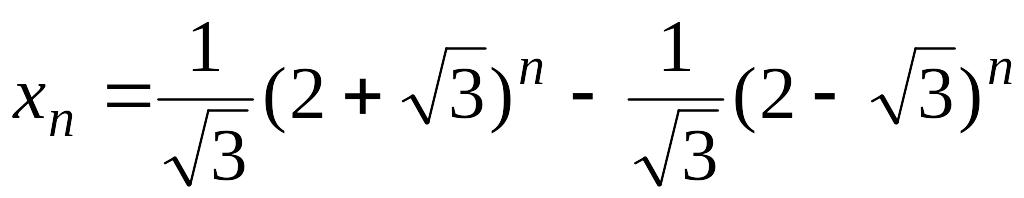для всех
.
Без
использования сделанного выше замечания
сделать такое пред-положение о виде
общего члена
рассматриваемой последовательности
было бы затруднительно. Во-первых, мы
использовали здесь тот факт, что
–
корни уравнения
.
Коэффициенты
мы нашли, решив систему уравнений
.
Приступим
к строгому доказательству сделанного
предположения. Для
это равенство проверяется непосредственно.
Предположим, что оно выполнено для
и
.
Докажем его справедливость для
.
Тогда в соответствии с принципом
математической индукции рассматриваемое
равенство будет верным для всех
.
.
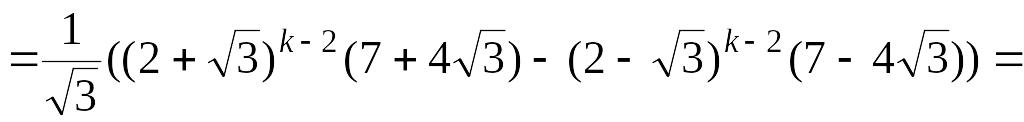
Таким образом, требуемое утверждение доказано. Перейдем к вычислению искомого предела. Используя сделанные выше обозначения, имеем
.
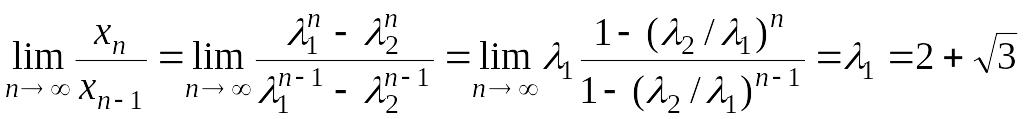Следующие два упражнения предлагаем выполнить самостоятельно.
Упражнение
5. Определить
константы
и
для последовательности Фибоначчи:
,
,
.
Вычислить величину золотого сечения:
.
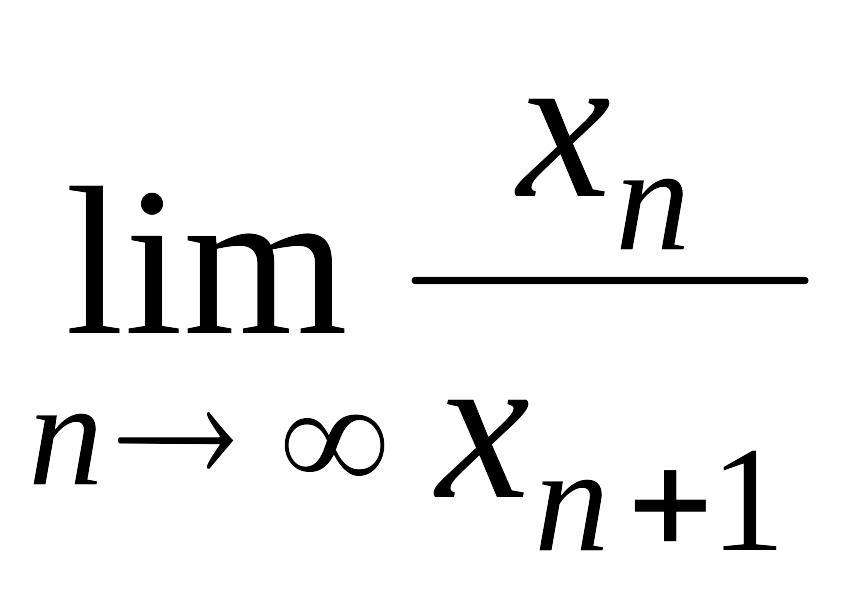Решение. Выполняется аналогично упражнению 4.
Упражнение 6. Доказать, что все элементы последовательности
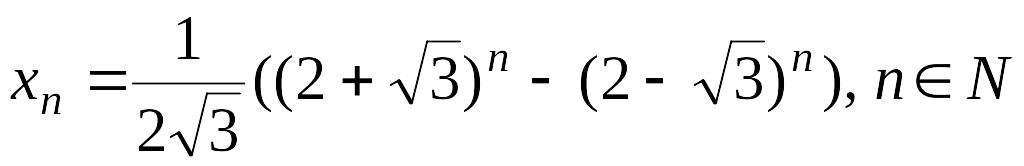
являются натуральными числами.
Решение. Выполняется аналогично упражнению 4.
Теорема
3 (Теорема Штольца).
Пусть последовательности
удовлетворяют условиям:
а)
для всех
;
б)
в)
существует конечный или бесконечный
предел
.
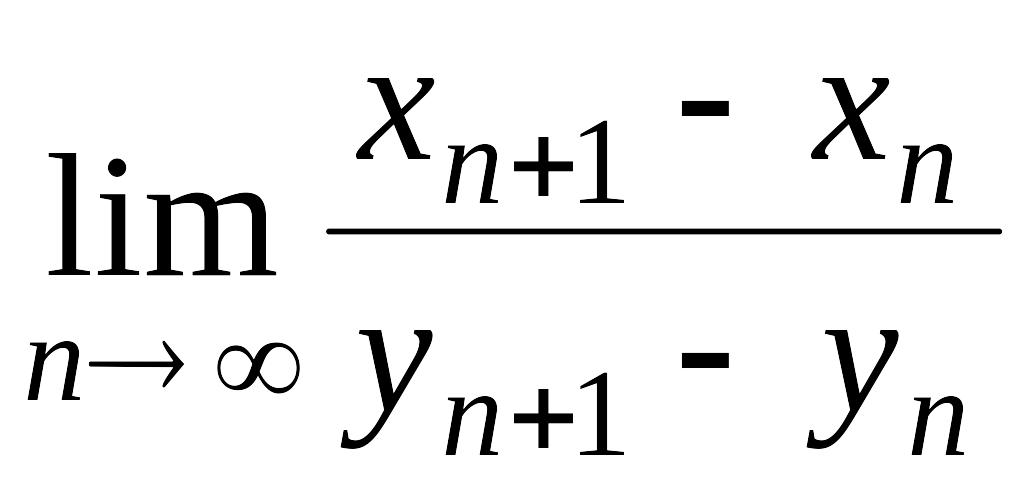Тогда
.
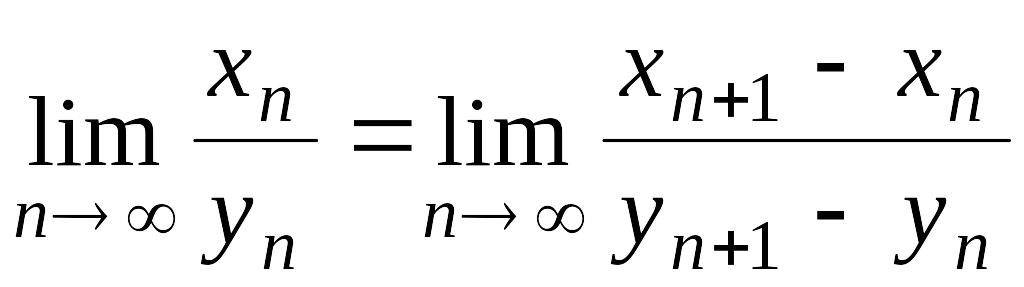Упражнение
7. Пусть
.
Показать, что
.
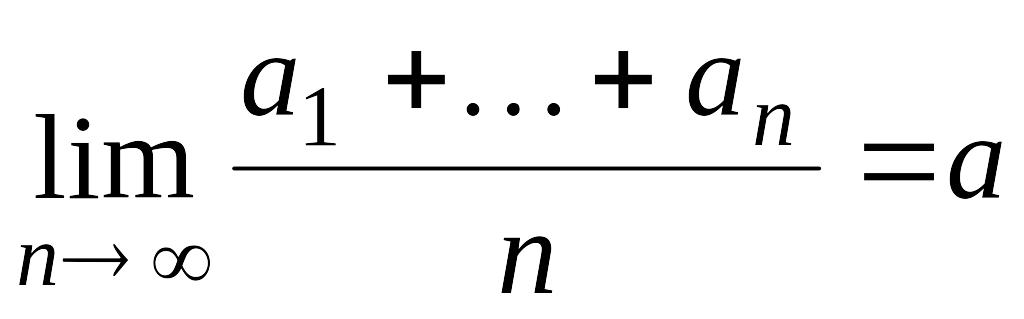Решение.
Полагая
,
,
получаем, что по-следовательность
удовлетворяет условиям а и б
теоремы 3. Условие в выполнено, так
как
.
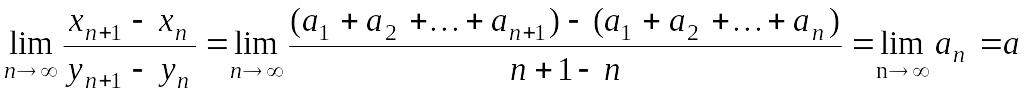Таким образом,
.
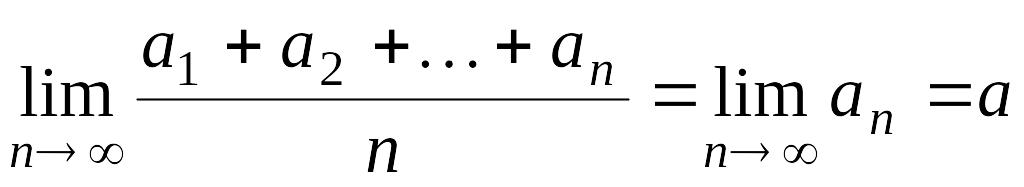Заметим,
что утверждение, обратное сформулированному
в упражнении 5, вообще говоря, неверно.
Например, для последовательности
:
,
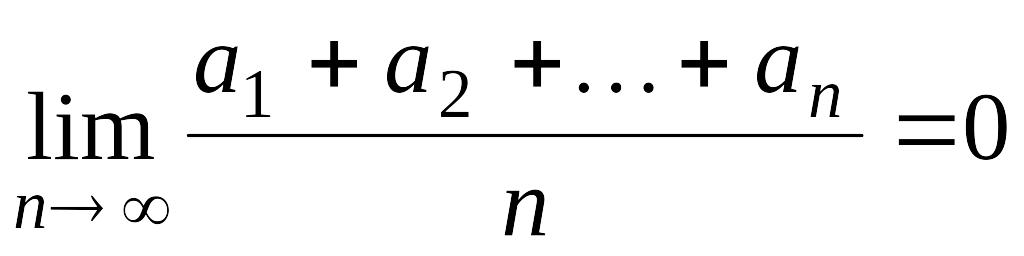а
не существует.
Упражнение
8. Найти предел последовательности
,
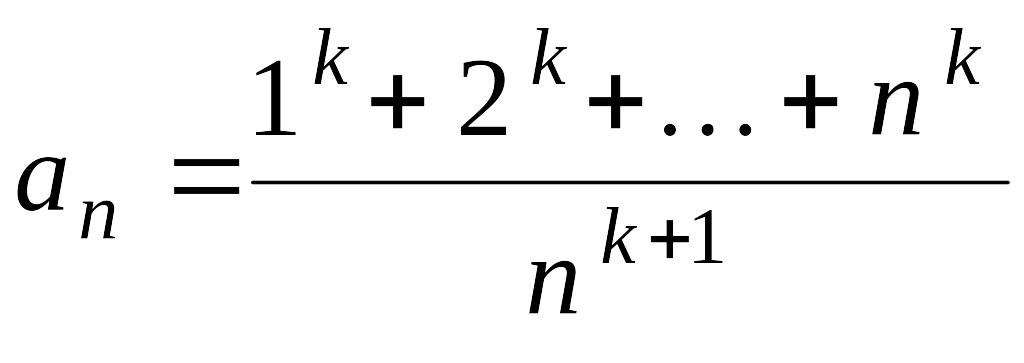где k – фиксированное натуральное
число.
Решение. Положим,
,
.
Тогда
,
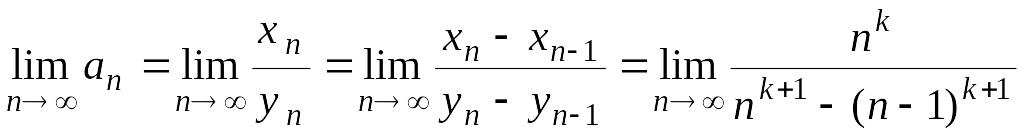если предел справа существует. Докажем существование этого предела.
Воспользовавшись формулой бинома Ньютона, получим
,
где троеточие заменяет сумму степеней n, меньших k, так, что
Поэтому
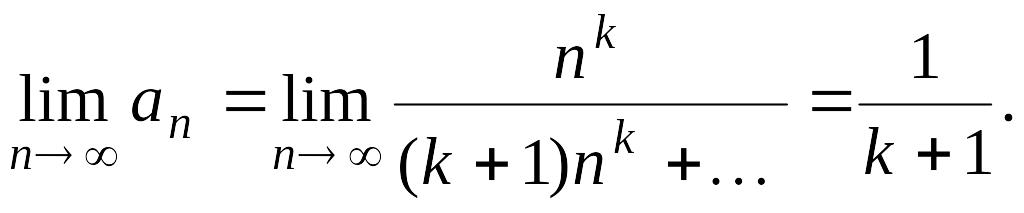
Упражнение
9.
Показать, что если
то
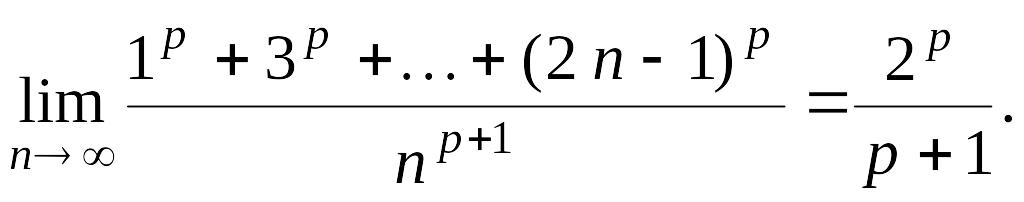
Решение. Выполнить самостоятельно.
Теорема 4. Пусть последовательности
удовлетворяют условиям:
а)
для всех
;
б)
.
Тогда последовательность
сходится и
.
Упражнение 10. Показать, используя теорему 4, что
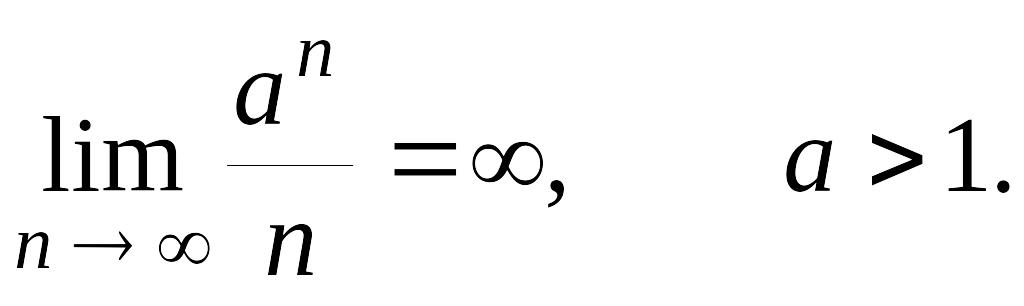
Решение.
По условию а представимо в виде
.
По формуле бинома Ньютона при
имеем
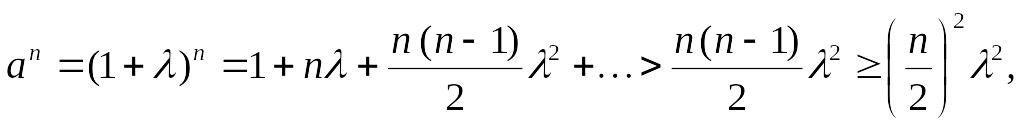
так как
при
.
Отсюда
при
получаем
.
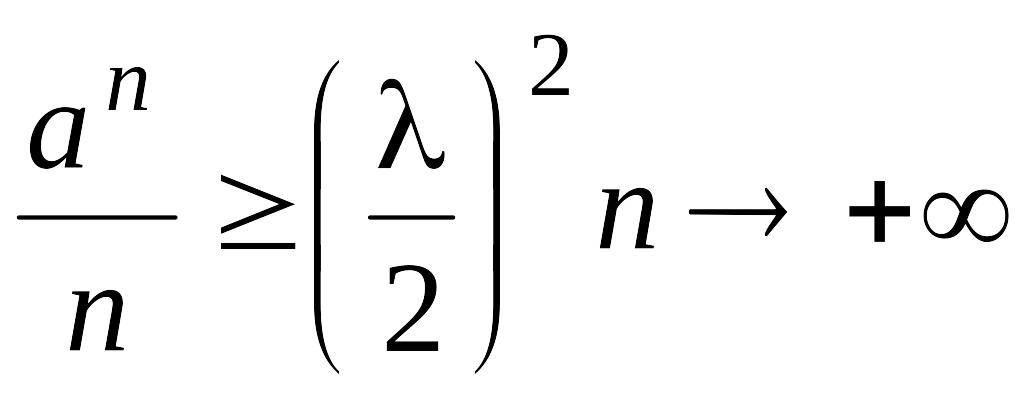Следовательно,
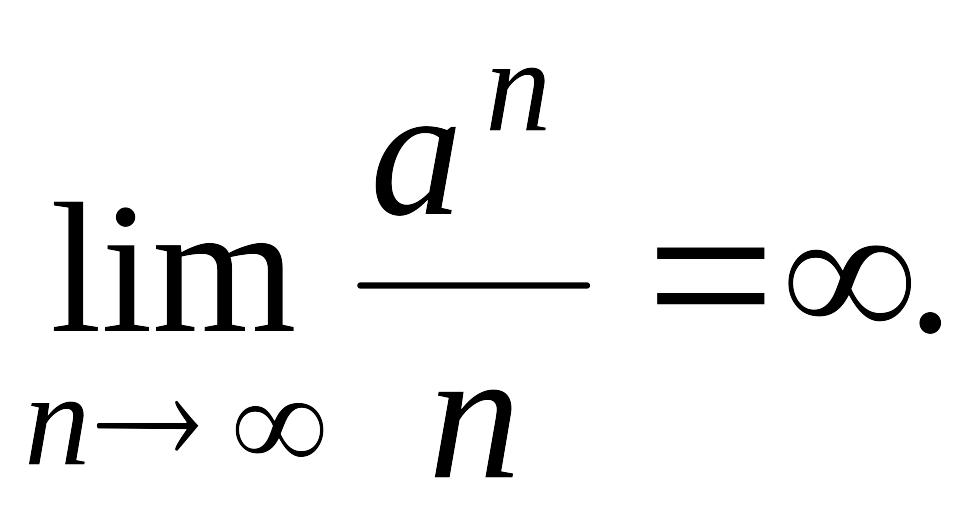
Упражнение 11. Используя рассмотренную выше технику, показать, что
.
Решение.
Поскольку
при любом
имеем
,
то
Отсюда
.
Так как
при
,
то
;
таким образом,
при
.
Следовательно,
,
и, значит,
.
Упражнение 12. Вычислить пределы последовательностей
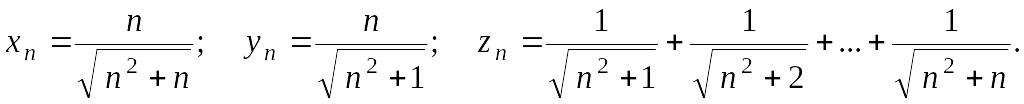
Решение.
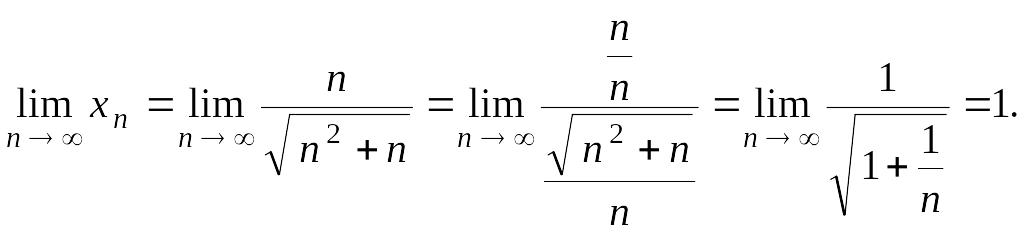
Аналогично
.
Для вычисления предела последовательности
заметим, что для всех
имеет
место неравенство
,
так как
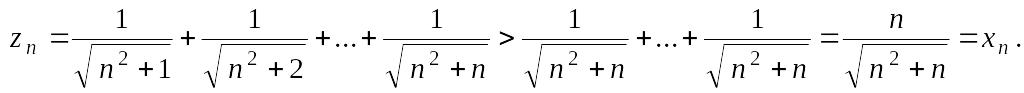
Аналогично
для всех
.
Таким образом,
и
.
По теореме
4
Вычисление пределов вида
,
если
,
если
с использованием
исключительно методов теории
последовательностей является, как
правило, достаточно трудоемкой задачей,
способ решения которой зависит от
конкретного вида последовательностей
,
.
Упражнение13.
Доказать, что при
выполнено равенство
Решение.
Из неравенства
при
и
следует
.
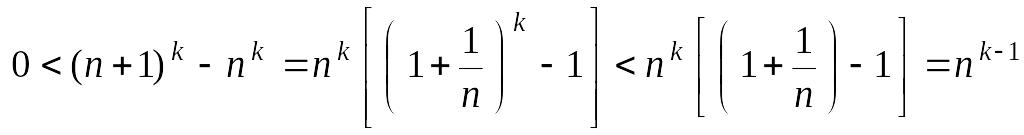Так
как
при
,
по теореме 4 получаем, что
.