
- •Часть 1
- •1. Линейная алгебра
- •1.1. Основные классы квадратных матриц
- •Задачи для самостоятельного решения
- •1.2. Определители. Ранг матрицы
- •1.2.1. Вычисление определителей
- •1.2.2. Вычисление ранга матриц
- •Задачи для самостоятельного решения
- •1.3. Обратная матрица
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Как изменится матрица , если совершить аналогичные преобразования со столбцами матрицы а?
- •1.4. Жорданова нормальная форма
- •1.5. Возведение матриц в степень. Нильпотентные матрицы. След матрицы
- •Задачи для самостоятельного решения
- •1.6. Многочлены
- •Задачи для самостоятельного решения
- •2. Введение в анализ
- •2.1. Метод математической индукции
- •Алгоритм метода математической индукции
- •Решение. Используем метод математической индукции.
- •Задачи для самостоятельного решения
- •2.2. Пределы последовательностей
- •Упражнение 14. Найти
- •Примеры решения задач
- •Пример 2. Пусть , . Найти .
- •Задачи для самостоятельного решения
- •1. Вычислить пределы:
- •2.3. Предел функции. Непрерывность
- •Примеры решения задач
- •Пример 8. Доказать, что если функция непрерывна на отрезке и имеет обратную функцию, то она монотонна на этом отрезке.
- •Задачи для самостоятельного решения
- •3.1. Производная функции. Вычисление производной по определению
- •Если он существует и конечен, называется правосторонней (левосторонней) производной и обозначается . Если существует производная , то будем говорить, что дифференцируема в точке .
- •Теорема 2. Если существует производная , то функция непрерывна в точке .
- •Примеры решения задач Пример 1. Пусть Подобрать коэффициенты a и b так, чтобы функция была дифференцируемой в точке .
- •Заметим, что как произведение бесконечно малой функции на ограниченную , после замены получим
- •Задачи для самостоятельного решения
- •1. Показать, что функция , где – непрерывная функция и , не имеет производной в точке .
- •2. Пусть
- •3.2. Вычисление пределов функций с использованием методов дифференциального исчисления
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •1. Вычислить пределы
- •3.3. Выпуклые и вогнутые функции. Точки перегиба
- •Важную роль при исследовании функции на выпуклость вверх (выпуклость вниз) играют точки, в которых происходит изменение направления выпуклости функции.
- •В этом разделе будут рассмотрены основные свойства выпуклых вниз (вверх) функций, заданных на отрезке .
- •Задачи для самостоятельного решения
- •3.4. Основные теоремы дифференциального исчисления
- •Примеры решения задач
- •Обратим внимание на то, что является точкой перегиба функции . Оказывается, что этот факт верен для любой дважды дифференцируемой функции.
- •Так как , то , что и требовалось доказать.
- •Задачи для самостоятельного решения
- •6. Исследование функции нескольких переменных на экстремум
- •7. Доказательство тождеств с использованием свойств дифференцирования
- •Задачи для самостоятельного решения
- •3.6. Производные высших порядков
- •Задачи для самостоятельного решения
- •Заключение
- •Часть 1
- •394006 Воронеж, ул. 20-летия Октября, 84
Задачи для самостоятельного решения
1. Разложить на линейные множители с комплексными коэффициентами многочлены:
а)
![]() ; б)
; б)
![]() ; в)
; в)
![]() .
.
2. Разложить на линейные и квадратичные множители с вещественными коэффициентами многочлены:
а)
;
б)
![]() ;
в)
;
в)
![]() .
.
3.
При каких а и b
многочлен
![]() имеет корень кратности два, отличный
от нуля.
имеет корень кратности два, отличный
от нуля.
4.
Доказать, что многочлен
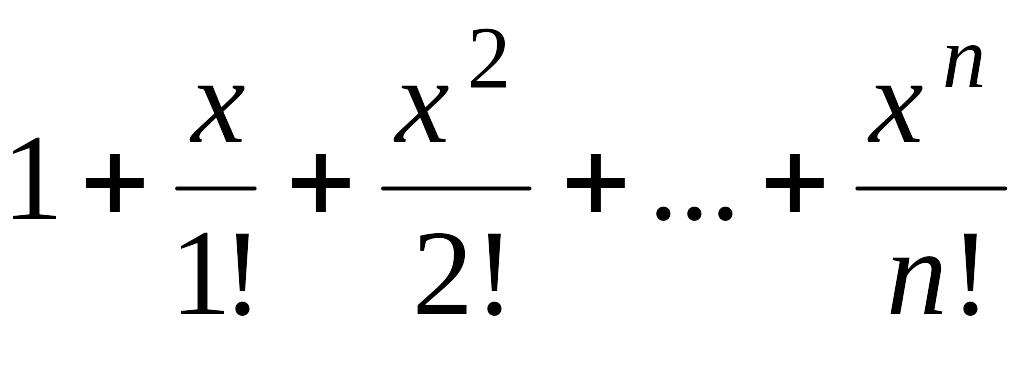 не имеет кратных корней.
не имеет кратных корней.
5.
Доказать, что многочлен
![]() делится на
делится на
![]() при всех
при всех
![]() .
.
6.
Показать, что многочлен
![]() не делится на
не делится на
![]() ни при каком значении параметров
ни при каком значении параметров
![]()
7.
Определить, при каких
![]() многочлен
многочлен
![]() делится на
делится на
![]() .
.
8.
Найти все значения
,
при которых многочлены
![]() и
и
![]() имеют общий корень.
имеют общий корень.
9. Найти многочлен наименьшей степени,
принимающий максимальное значение 6
при
![]() и минимальное значение 2 при
и минимальное значение 2 при
![]() .
.
10. Определить значения параметров
p и q,
при которых многочлен
![]() имеет три различных вещественных корня.
имеет три различных вещественных корня.
11. Пусть многочлен
имеет только вещественные корни.
Доказать, что если а – кратный корень
многочлена
![]() ,
то
,
то
![]() .
.
12. Доказать, что если
и
– многочлены степени n,
то либо
![]() ,
либо степень многочлена
,
либо степень многочлена
![]() не меньше n.
не меньше n.
13. Определить количество вещественных
корней многочлена
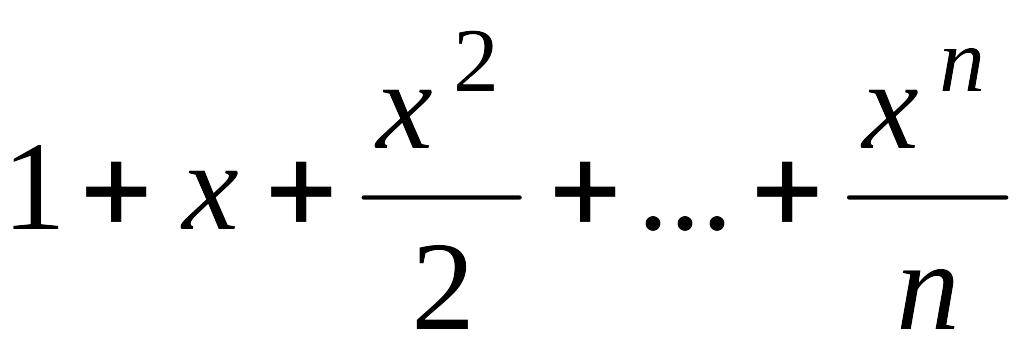 .
.
14.
Показать,
что для заданных не равных между собой
действительных чисел
![]() и
и
![]() и натурального
найдутся единственные многочлены
и натурального
найдутся единственные многочлены
![]() и
и
![]() ,
такие, что
,
такие, что
![]() ,
,
![]() ,
,
![]() ;
вывести отсюда равенства
;
вывести отсюда равенства
![]() ,
,
![]() .
Будут ли выполняться последние неравенства
, если не накладывать условий на степени
многочленов?
.
Будут ли выполняться последние неравенства
, если не накладывать условий на степени
многочленов?
15.
Решить упражнение 3 без использования
результанта
![]()
2. Введение в анализ
2.1. Метод математической индукции
Этот метод используется для того, чтобы доказать, что некоторое утверждение верно для всякого натурального числа и применяется в различных разделах математики.
Алгоритм метода математической индукции
1. Непосредственными вычислениями устанавливается, что утверждение верно для .
2.
Делается предположение, что утверждение
верно для некоторого
или для всех
![]() .
.
3.
Исходя из сделанного предположения,
доказывается, что утверждение верно
для
![]() .
Отсюда следует, что утверждение верно
для всех
.
Отсюда следует, что утверждение верно
для всех
![]() .
.
Пример
1. Доказать,
что
![]() .
.
Решение. Используем метод математической индукции.
1.
Если
,
то
![]() .
.
2. Предположим, что утверждение верно для , т.е.
![]() .
.
3. Для с использованием предположения 2 получаем
![]()
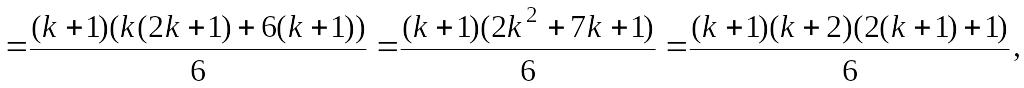
что и требовалось доказать.
Бесконечной
числовой последовательностью (или
просто числовой последовательностью)
называется функция
![]() ,
определенная на множестве всех натуральных
чисел 1,2,…, n,…
. Значения последовательности
,
определенная на множестве всех натуральных
чисел 1,2,…, n,…
. Значения последовательности
![]() называются ее членами.
называются ее членами.
Последовательность
иногда обозначают так:
![]() .
Это означает, что задана последовательность
с общим членом
.
Это означает, что задана последовательность
с общим членом
![]() .
По данному общему члену всегда можно
найти любой член последовательности
.
По данному общему члену всегда можно
найти любой член последовательности
![]() ,
подставив в
вместо
n
число k.
Ниже приведены примеры последовательностей,
причем сначала приведена форма записи
,
а затем записаны первые члены:
,
подставив в
вместо
n
число k.
Ниже приведены примеры последовательностей,
причем сначала приведена форма записи
,
а затем записаны первые члены:
1)
|
5)
|
2)
|
6)
|
3)
|
7)
|
4)
|
|
Пример
2.
Последовательность
положительных чисел
![]() ,
,![]() удовлетворяет
условию
удовлетворяет
условию
![]() для всех
.
Доказать, что для любого
имеет место оценка
для всех
.
Доказать, что для любого
имеет место оценка
![]() .
.
Решение.
1.
Если
![]() ,
то
,
то
![]() .
Откуда
.
Откуда
![]() .
Если
.
Если
![]() ,
то
,
то
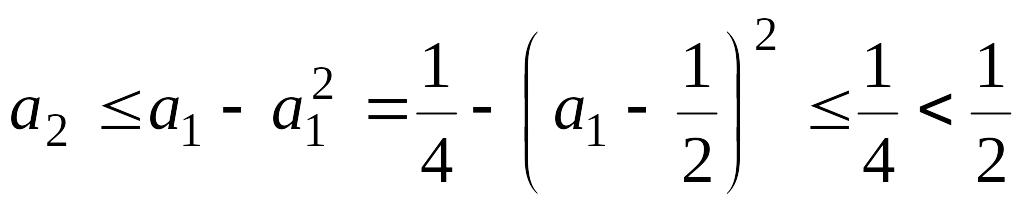 .
.
2.
Предположим, что
![]() для произвольного
для произвольного
![]() .
.
3.
Докажем, что выполнено неравенство
![]() .
.
Во-первых,
покажем, что функция
![]() возрастает на
возрастает на
![]() .
Возьмем
.
Возьмем
![]() .
Тогда
.
Тогда
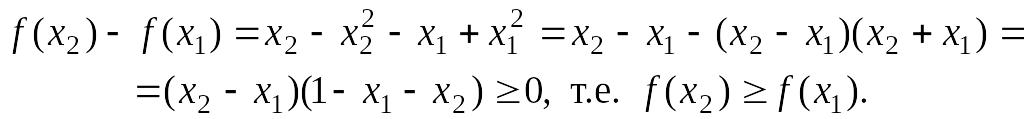
Отсюда и из того, что , в силу предположения 2 получаем
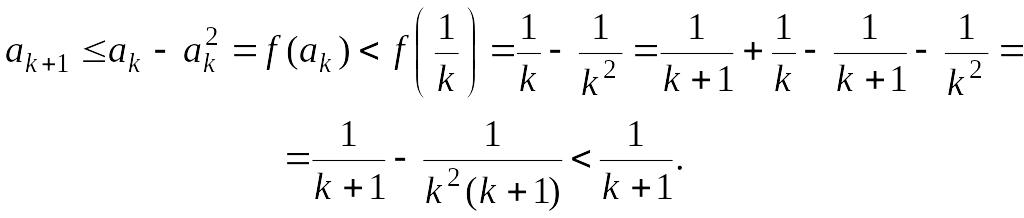
Пример 3 (Бином Ньютона)
Обозначим
![]() для
для
![]() ,
,
![]() (запись n!
читается «n-факториал»);
(запись n!
читается «n-факториал»);
![]() ,
,
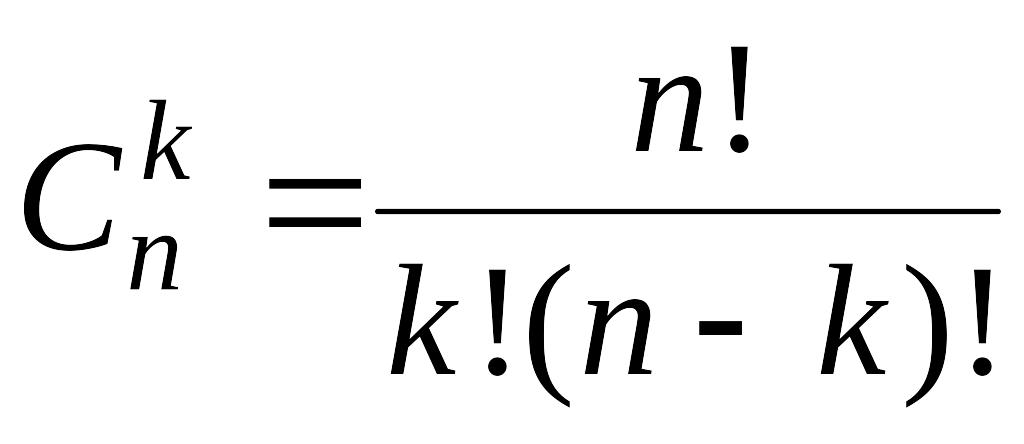 .
.
Биномом Ньютона называется равенство
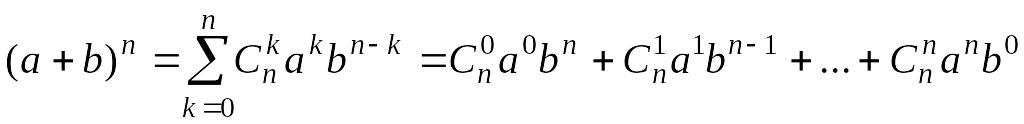 .
.
Справедливость
этого равенства для всех
![]() и
доказывается
методом математической индукции.
и
доказывается
методом математической индукции.
При
![]() доказываемое равенство принимает вид
доказываемое равенство принимает вид
![]() .
Последнее равенство верно, так как
.
Последнее равенство верно, так как
![]() .
Предположим, что равенство верно для
n=k.
Тогда для n=k+1
получаем
.
Предположим, что равенство верно для
n=k.
Тогда для n=k+1
получаем
![]()
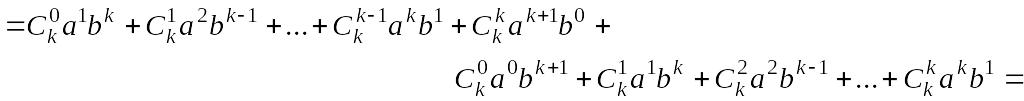
![]() Так как для любых
Так как для любых
![]() выполнены равенства
выполнены равенства
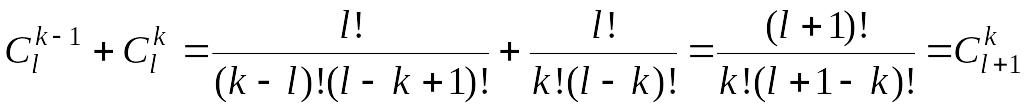 ,
,
то окончательно получаем
![]()
Таким образом, равенство полностью доказано.
С другими примерами использования метода математической индукции читатели столкнутся во многих следующих ниже разделах пособия.
