2. Положительные ряды

Имеется большое количество достаточных признаков для изучения сходимости положительных рядов.

I. Признаки сравнения.

Признак 1. Если даны два положительных ряда и , причем, начиная с некоторого номера ,

, (4)

то:

а) из сходимости ряда с бóльшими членами следует сходимость ряда с меньшими членами;

б) из расходимости ряда с меньшими членами следует расходимость ряда с бóльшими членами.

Признак 2. Если для рядов с положительными членами ,

(5)

то рассматриваемые ряды сходятся или расходятся одновременно.

Для признаков сравнения используют стандартные (так называемые обобщённо-гармонические) ряды

, (6)

которые сходятся при и расходятся при .

II. Признаки, сравнивающие положительный ряд по скорости сходимости с геометрической прогрессией.

1. Признак Даламбера. Пусть существует конечный предел:

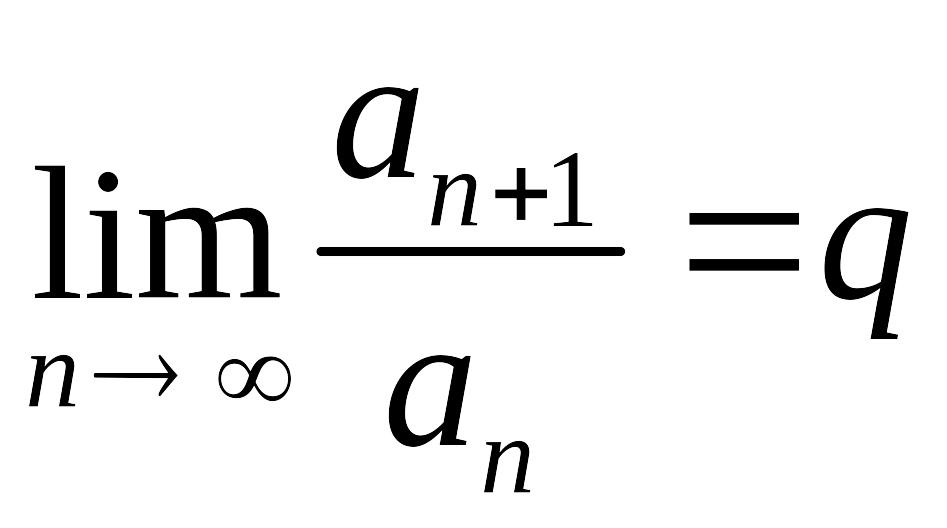(7)

или

2. Радикальный признак Коши. Пусть существует конечный предел:

. (8)

Тогда ряд

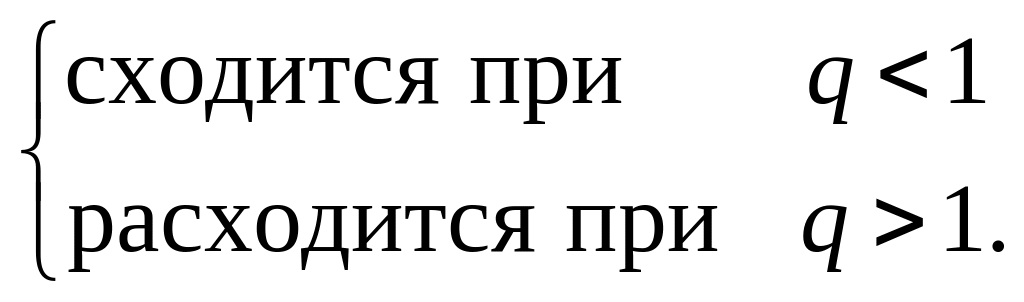(9)

Если , то эти признаки не дают ответа на вопрос о сходимости исследуемого ряда. В этом случае следует воспользоваться другим признаком.

III. Интегральный признак Коши. Если члены положительного ряда представимы в виде , где функция непрерывна и монотонно убывает при , то ряд (1) и соответствующий несобственный интеграл

(10)

сходятся или расходятся одновременно.

Возникает вопрос: когда какой признак применить? Рекомендуем:

1. Необходимый признак применять для доказательства расходимости ряда, если легко видеть, что предел общего члена не равен нулю или вообще не существует.

2. Если члены ряда меняются быстро (типа показательной функции 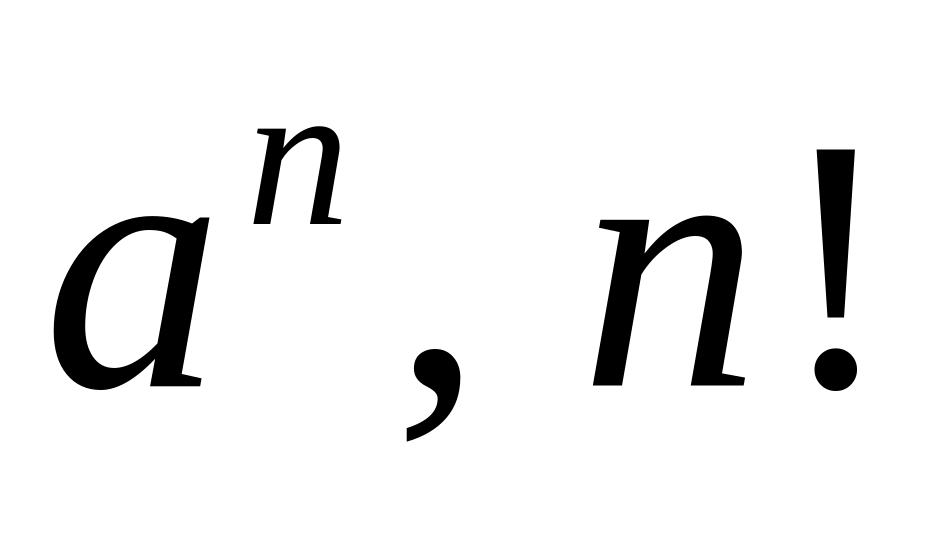и так далее) или заданы рекуррентным соотношением, то применять признак Даламбера; радикальный признак Коши рекомендуется применять, когда члены ряда представляют собой выражение в степени, зависящей от .

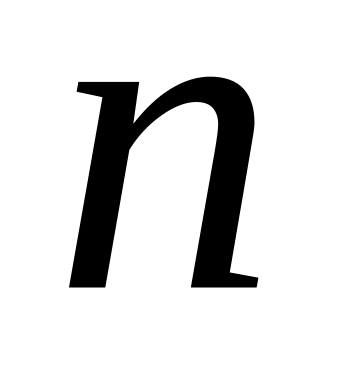3. Если члены ряда меняются медленно (типа степенной функции 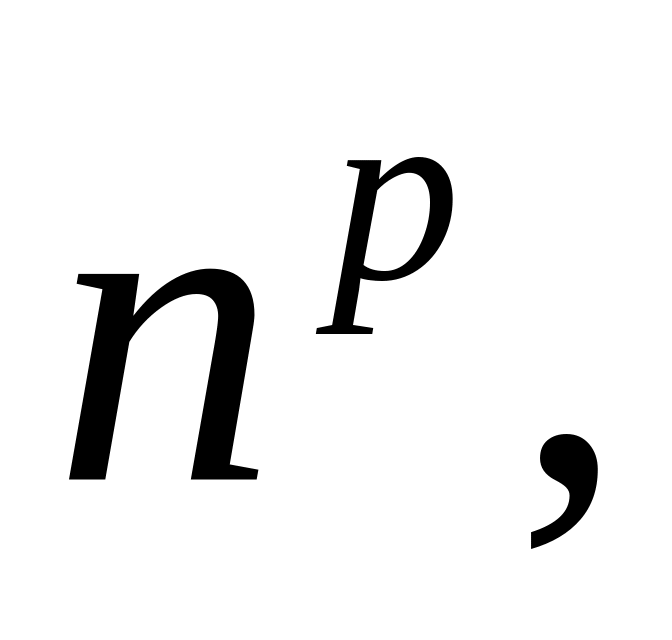логарифмической 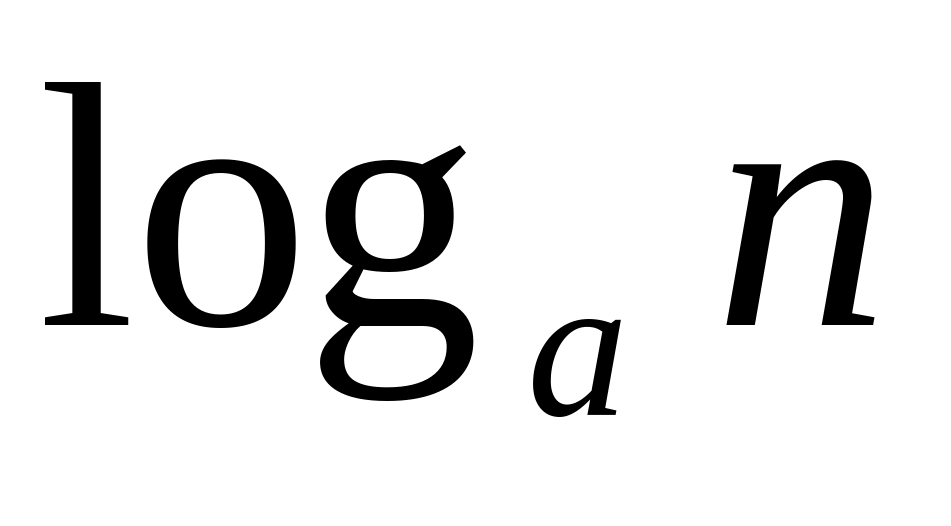и так далее), то применять или признаки сравнения (если видно с каким табличным рядом сравнивать), или интегральный признак Коши.

Пример 2. Исследовать на сходимость ряд .

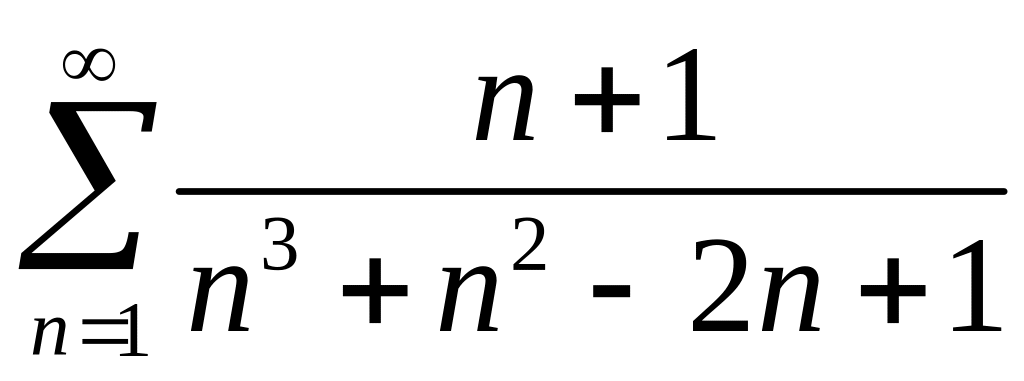Члены ряда при больших мало отличаются от , поэтому воспользуемся первым признаком сравнения, взяв в качестве табличного сходящийся ряд . Проверим, что : - неравенство не выполняется при натуральных . Увеличим члены табличного ряда в два раза и проверим, что :

.

Последнее неравенство справедливо при всех натуральных . Так как члены искомого ряда не превосходят членов сходящегося ряда , то по первому признаку сравнения данный ряд сходится.

Этот же пример можно решить, используя второй из приведённых признаков сравнения. Взяв в качестве табличного тот же сходящийся ряд , получим:

По второму признаку сравнения рассматриваемый ряд сходится.

Пример 3. Исследовать на сходимость ряд .

Применим признак Даламбера. Так как , то .

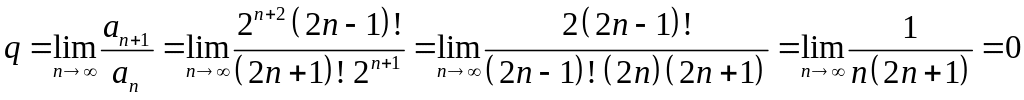Так как , то по признаку Даламбера данный ряд сходится.

Пример 4. Исследовать на сходимость ряд .

Воспользуемся интегральным признаком Коши:

.

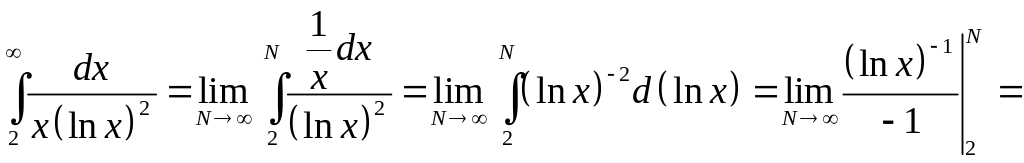
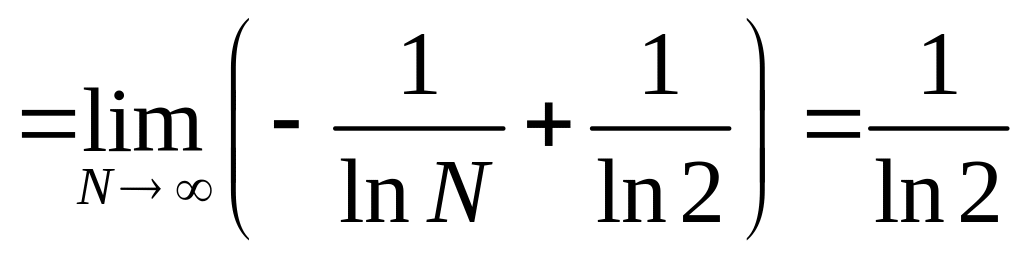Так как соответствующий интеграл сходится, то и данный ряд сходится.

Пример 4*. Исследовать на сходимость ряд .

Так как при , то для членов нашего ряда справедлива оценка .

Применим к ряду интегральный признак Коши:

.

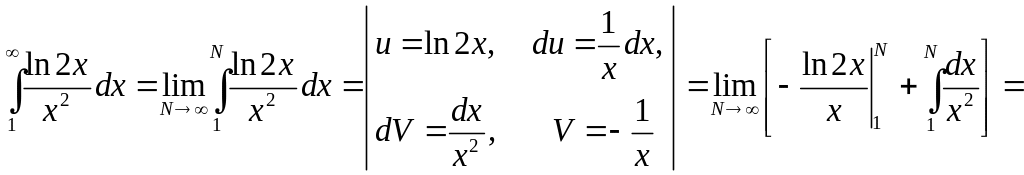
Так как несобственный интеграл сходится, то и соответствующий вспомогательный ряд сходится, а следовательно, и ряд тоже сходится. В силу первоначальной оценки искомый ряд по первому признаку сравнения тоже сходится.

Пример 5. Исследовать на сходимость ряд .

Так как при больших члены ряда , то воспользуемся вторым признаком сравнения, взяв табличный ряд .

Тогда

.

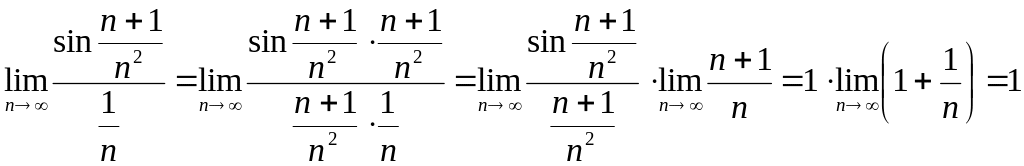Так как выбранный для сравнения табличный гармонический ряд расходится , то и данный ряд расходится.

Пример 5*. Исследовать на сходимость ряд .

Сначала оценим дробь:

.

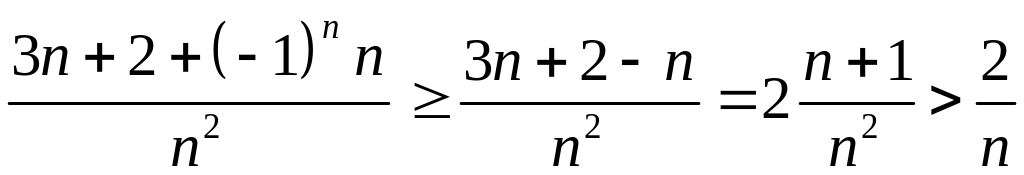Так как строго возрастающая функция, то

.

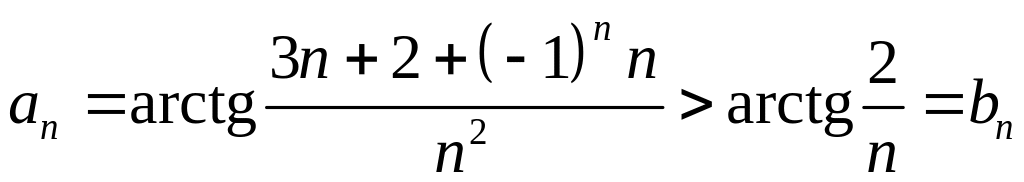Сравним вспомогательный ряд 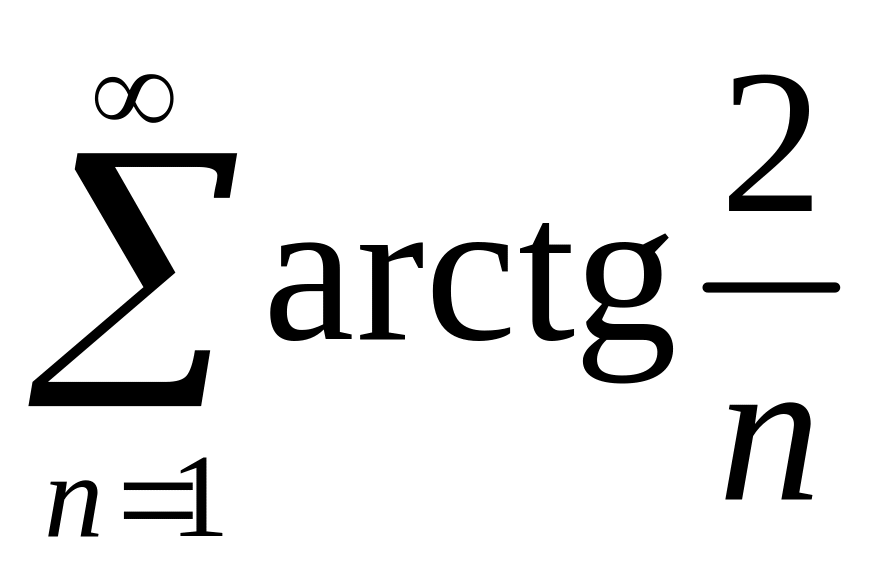с гармоническим рядом.

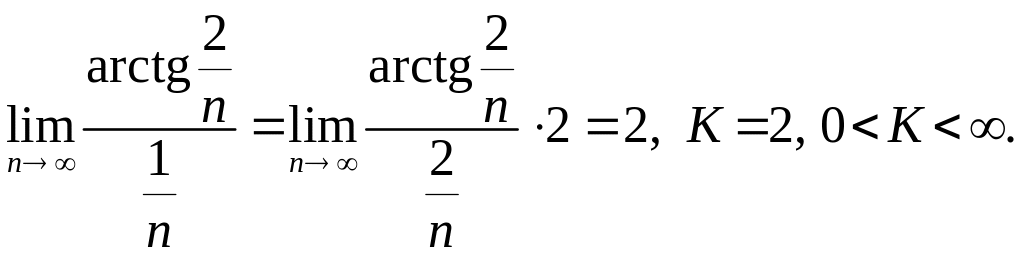
Так как гармонический ряд расходится, то по второму признаку сравнения вспомогательный ряд тоже расходится. В силу выше приведенной оценки искомый ряд по первому признаку сравнения тоже расходится.

Пример 6. Исследовать на сходимость ряд .

ъПрименим радикальный признак Коши:

.

Так как , то по радикальному признаку Коши данный ряд расходится.