5. Функции случайных величин

Если Х – дискретная случайная величина с рядом распределения

Табл.5.1.

Xi	X1	X2	………	Xn
Pi	P1	P2	………	Pn

а величина Y связана функциональной зависимостью , то математическое ожидание величины Y равно:

а дисперсия выражается формулой:

Если Х – непрерывная случайная величина с плотностью распределения f(x), то математическое ожидание величины Y равно:

.

а дисперсия выражается любой из формул:

.

Если с – не случайная величина, то M[c]=c ; D[c]=0.

Если с – не случайная величина, Х – случайная, то:

.

Теорема сложения математических ожиданий

Математическое ожидание суммы случайных величин равно сумме их математических ожиданий: M[X+Y]=M[X]+M[Y].

И более общая формула: .

М атематическое ожидание линейной функции нескольких случайных величин: ;

где – не случайные коэффициенты, равно той же линейной функции от их математических ожиданий:

;

где i = 1,2,…,n.

Теорема умножения математических ожиданий.

Математическое ожидание произведения двух случайных величин X,Y выражается формулой

где – корреляционный момент величин X,Y . В другом виде можно записать или имея в виду, что

Математическое ожидание произведения двух некоррелированных случайных величин X,Y равно произведению их математических ожиданий: M[XY]=M[X] M[Y].

Д исперсия суммы двух случайных величин X,Y выражается формулой:

Дисперсия суммы двух некоррелированных случайных величин X,Y равно сумме их дисперсий D[X+Y]=D[X]+D[Y].

И вообще для некоррелированных случайных величин:

Дисперсия линейной функции нескольких случайных величин:

г де – не случайные величины, а величины

некоррелированны.

Для нескольких случайных величин:

Пример:

Имеются две случайные величины X,Y , связанные между собой соотношением Y=2-3X.

Числовые характеристики величины Х заданы: .

Найти:

1) Математическое ожидание и дисперсию величины Y ;

2) Корреляционный момент и коэффициент корреляции величин X,Y.

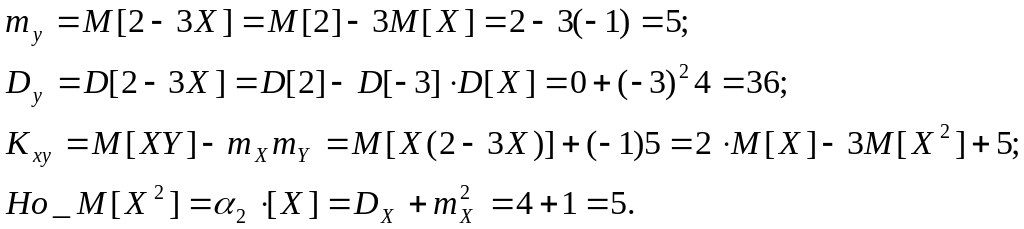
Тогда .

Что естественно, т.к. X и Y связаны между собой линейной зависимостью.