
- •1. Основные понятия
- •Основные определения
- •Событие, вероятность события (частота события)
- •2. Случайные величины и законы распределения
- •Числовые характеристики случайных величин
- •Моменты для непрерывных величин:
- •2.2. Законы распределения случайной величины
- •I f(X) c α β X X I) равномерный
- •2.3. Определение законов распределения случайных величин
- •3. Системы случайных величин
- •3.1. Числовые характеристики системы двух случайных величин
- •3.2. Числовые характеристики системы нескольких случайных величин
- •Распределение Пуассона:
- •Л огнормальный закон распределения:
- •Нормальный закон распределения:
- •4.2. Распознавание в многомерном пространстве
- •Платежная матрица:
- •4.3. Параметрические методы распознавания
- •5. Функции случайных величин
- •Теорема сложения математических ожиданий
- •Теорема умножения математических ожиданий.
- •И вообще для некоррелированных случайных величин:
- •Для нескольких случайных величин:
- •6. Случайные функции
- •6.1. Законы распределения случайной величины
- •6.2. Корреляционная функция и ее свойства
- •Основные свойства корреляционной функции:
- •6.3. Пример случайной функции
- •Математическое ожидание случайной функции X(t) будет равно
- •Дисперсия случайной функции X(t) равна:
- •6.4.Cпектральные плотности
- •Введем понятие «плотность» дисперсии
- •На рис.6.2 показана спектральная плотность
- •Преобразование случайной функции линейной системой
- •Применение теории случайных функций к задачам анализа и синтеза
- •7. Прикладные задачи теории вероятности
- •7.1. Определение статистических характеристик
- •7.2. Нахождение функциональной зависимости
- •С оответственно:
- •7 .3. Линейная функция многих переменных Вводится новый набор переменных
- •Список литературы
- •Введение 3
3. Системы случайных величин
Если мы имеем две
величины
![]() и
и
![]() ,
то:
,
то:
![]() - интегральный
закон;
- интегральный
закон;
![]() - плотность
распределения
- плотность
распределения
Свойства
![]() аналогичны тем, что были для
аналогичны тем, что были для
![]()
![]() ;
;
![]() ;
;
![]() .
.
Условные законы
распределения
![]() и
и
![]() это закон распределения случайной
величины х фикси-значении y.
это закон распределения случайной
величины х фикси-значении y.
Зависимые и
независимые случайные величины – Y
не зависит от X,
если
![]() не зависит от значений
.
не зависит от значений
.
![]() .
.
Для независимых
случайных величин
![]() - это необходимое и достаточное условие
независимости
- это необходимое и достаточное условие
независимости
![]() и
и
![]() .
.
3.1. Числовые характеристики системы двух случайных величин
Начальный момент
![]() ;
;
Центральный момент
![]() .
.
![]() - математические
ожидания произведений
- математические
ожидания произведений
![]() в степенях
в степенях
![]()
![]() - порядок системы
случайных величин.
- порядок системы
случайных величин.
Легко записать формулы для непрерывных и дискретных случайных величин:
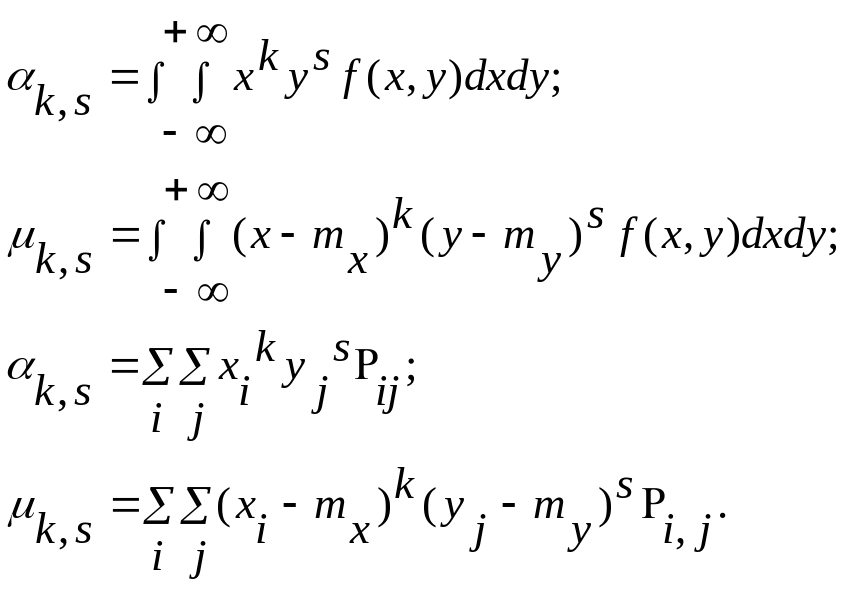
Наиболее часто используют следующие характеристики:
а)![]() начальные моменты первого порядка;
начальные моменты первого порядка;
б)![]() центральные моменты;
центральные моменты;
(Здесь
![]() и
и
![]() )
)
в)
![]() корреляционный момент.
корреляционный момент.
Если
и
независимы, то для них
![]() и тогда
и тогда
![]() .
.
г) Обычно используют нормированное значение корреляционного момента:
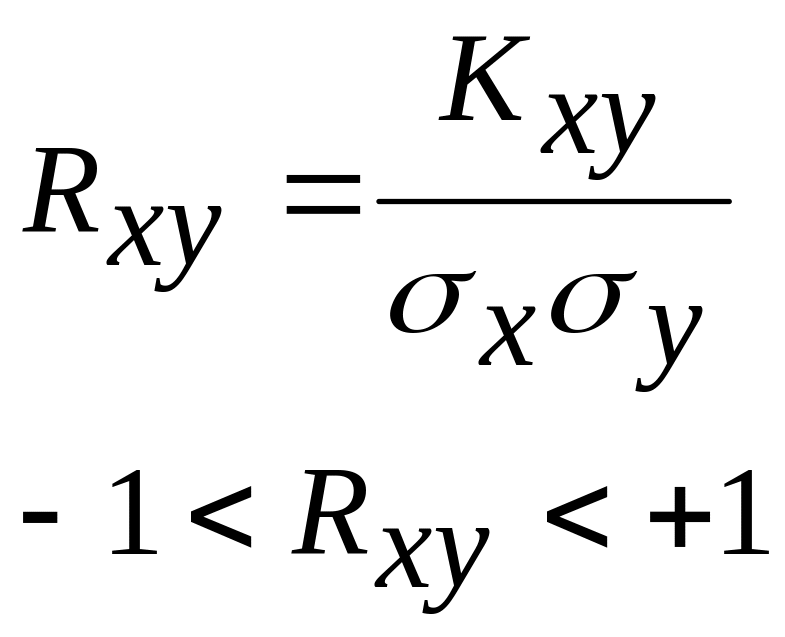 - коэффициент
корреляции;
- коэффициент
корреляции;
Коэффициент корреляции характеризует точность линейной связи:
![]() .
.
Чем точнее линейная
связь (меньше разброс), тем ближе
![]() к |1|.
к |1|.
3.2. Числовые характеристики системы нескольких случайных величин
Если имеем
![]() - n случайных величин, то минимальное
число характеристик для них:
- n случайных величин, то минимальное
число характеристик для них:
n математических операций
 ;
;n дисперсий
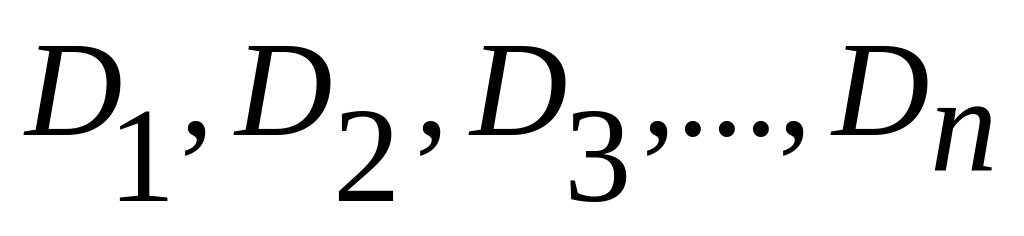 ;
;n(n-1) корреляционных моментов:
![]()
![]()
где
![]() для характеристики попарной корреляции
случайных величин.
для характеристики попарной корреляции
случайных величин.
Т ак
как,
ак
как,
![]() ,
то удобно все дисперсии и корреляционные
моменты поместить в одной матрице:
,
то удобно все дисперсии и корреляционные
моменты поместить в одной матрице:
Так как
![]() ,
то матрица симметрична относительно
главной диагонали. Если
,
то матрица симметрична относительно
главной диагонали. Если
![]() -
независимые величины, то все элементы,
кроме главной диагонали равны нулю:
-
независимые величины, то все элементы,
кроме главной диагонали равны нулю:
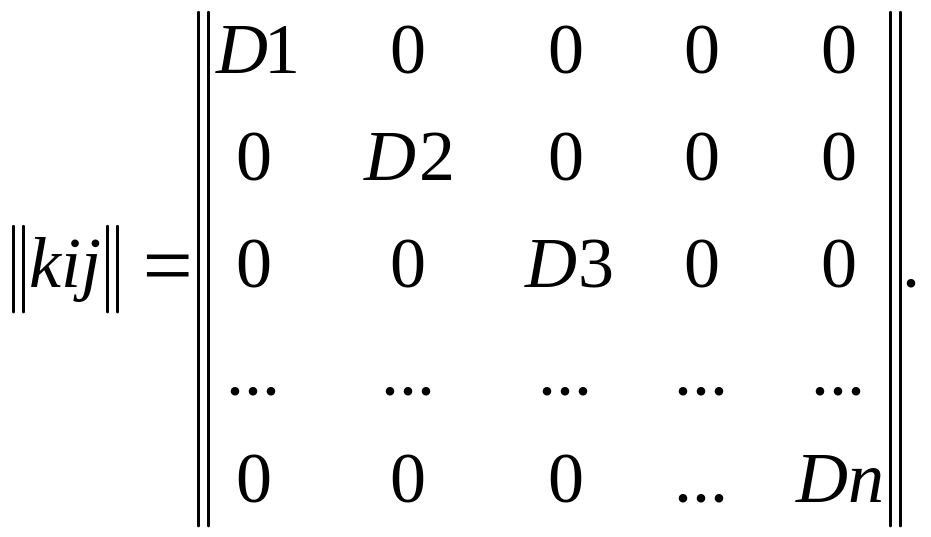
Если осуществить
нормировку (разделить на
![]() ),
то получим матрицу коэффициентов
корреляции симметричную относительно:
),
то получим матрицу коэффициентов
корреляции симметричную относительно:
3 .3.
Примеры законов распределения двух
случайных величин.
.3.
Примеры законов распределения двух
случайных величин.
Распределение Релея.
Для независимых
случайных величин:
![]()
![]() при
при
![]() ;
;
![]()
Распределение Пуассона:
![]()
при ;
![]()
![]()
![]() - коэффициент
корреляции;
- коэффициент
корреляции;
![]() - дисперсии;
- дисперсии;
![]() - переменные целочисленные.
- переменные целочисленные.
Л огнормальный закон распределения:
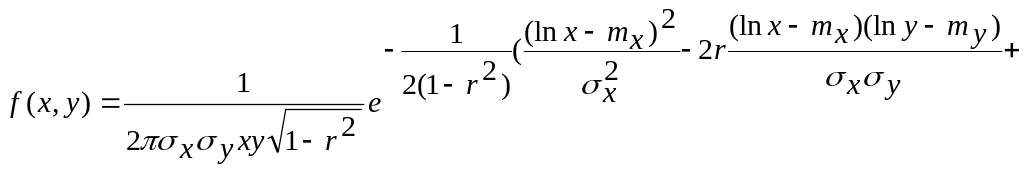
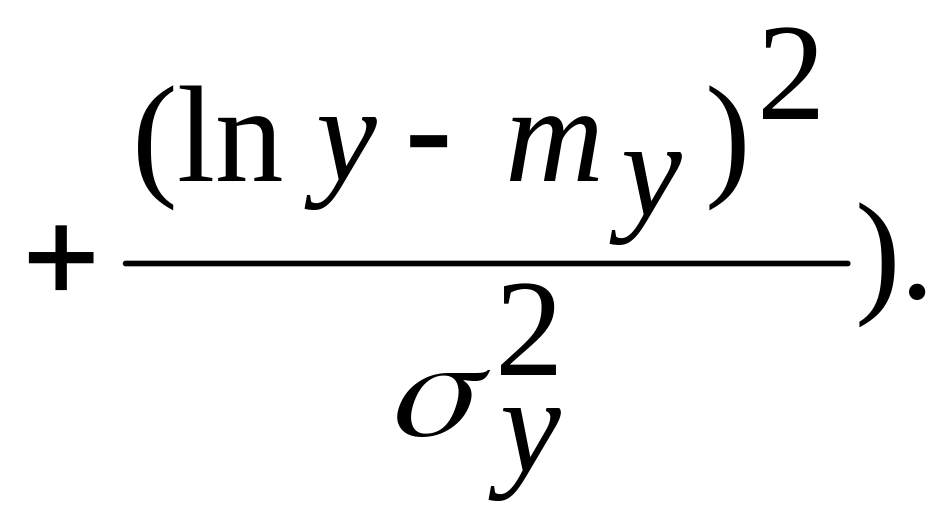
Нормальный закон распределения:

4. Распознование состояний в одно и многомерном случае
4.1. Распознавание двух состояний по одному признаку
вероятн.
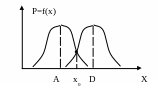
![]() Состояние А:
Состояние А:
![]() распред.
распред.
вероятн.
Рис. 4.1. Распознавание
двух состояний по
одному
признаку
![]()
![]() -распред.
-распред.
Введем отношение вероятностей:
![]() (если неизвестная
точка
(если неизвестная
точка
![]() обозначена
обозначена
![]() ).
).
Возможны несколько критериев распознавания:
Критерий максимального правдоподобия, т. е. верна та гипотеза, для которой вероятность больше (критерий Вальда):
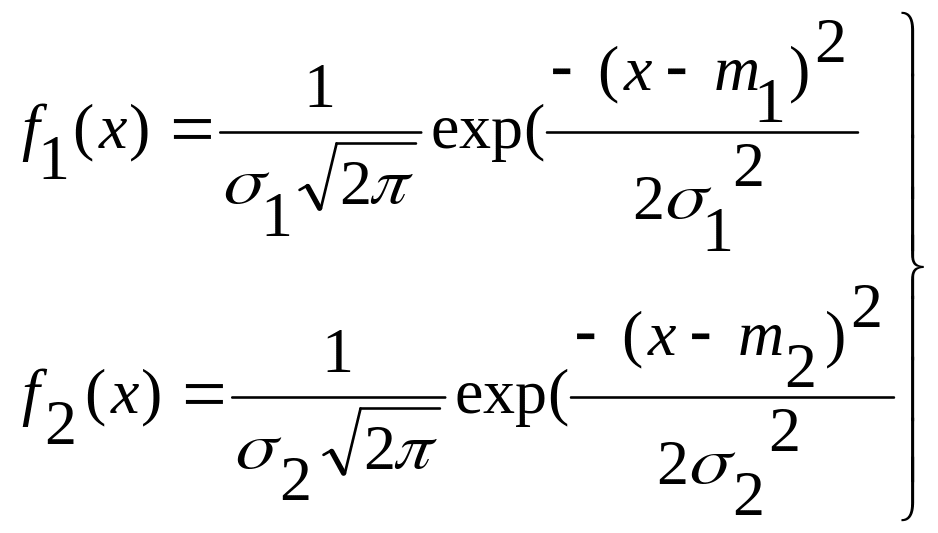 - априорные
вероятности;
- априорные
вероятности;
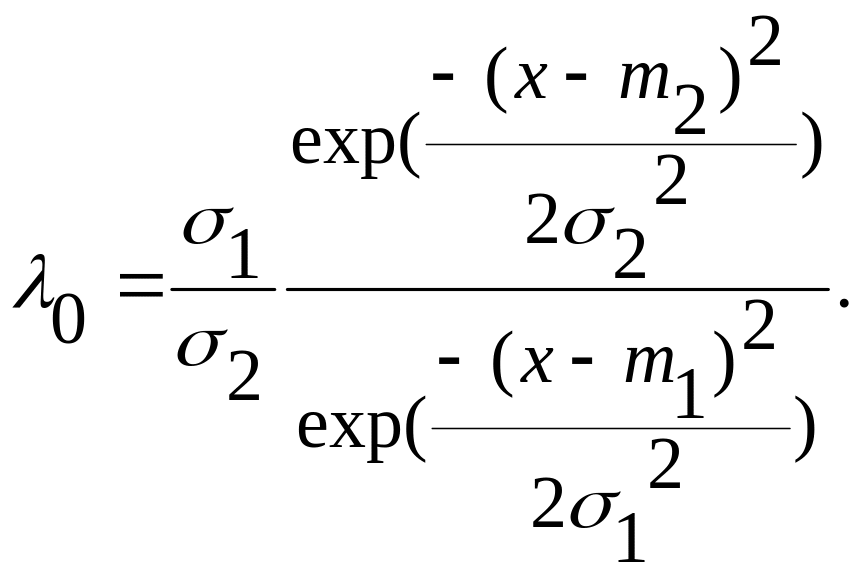
Для неизвестной
точки
![]() :
:
П![]() рологарифмируем
и найдем корни квадратного уравнения:
рологарифмируем
и найдем корни квадратного уравнения:
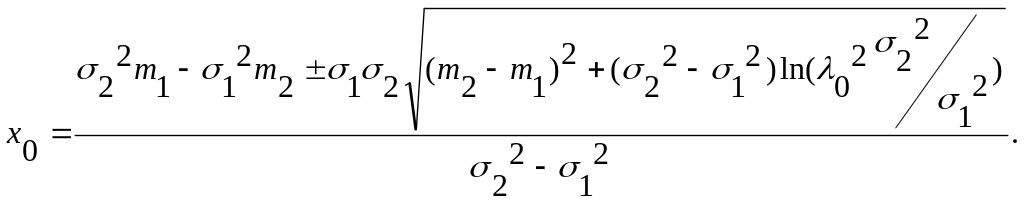
а) частный случай:
Если,
![]() ,
то получаем:
,
то получаем:
![]()
б) частный случай:
Если пограничная
точка
![]() соответствует равным вероятностям, то
соответствует равным вероятностям, то
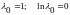
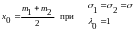 и
получаем
и
получаем
2
A
x0
B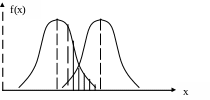 )
Критерий с взвешенными оценками
(Неймана-Пирсона)Задана матрица С
стоимости правильных и неправильных
решений отправляющие свойства препарата;
нападение противника; смертельный исход
лечения).
)
Критерий с взвешенными оценками
(Неймана-Пирсона)Задана матрица С
стоимости правильных и неправильных
решений отправляющие свойства препарата;
нападение противника; смертельный исход
лечения).
Рис. 4.2. Критерий
Неймана-Пирсона
![]()
![]()
![]()
![]() - потери (затраты)
при правильных;
- потери (затраты)
при правильных;
![]() решениях
решениях
![]() - потери (затраты)
при неправильных решениях..
- потери (затраты)
при неправильных решениях..
С![]() оответственно,
различают ошибки I рода (объект относиться
к классу 1 (А), а его отнесли к классу 2
(В) и ошибки второго (II) рода (класс 2
отнесли к классу 1).
оответственно,
различают ошибки I рода (объект относиться
к классу 1 (А), а его отнесли к классу 2
(В) и ошибки второго (II) рода (класс 2
отнесли к классу 1).
![]()
При многократном определении (классификации), средние потери находят как:
![]()
Если найти![]() (min потерь) и приравнять к нулю, то:
(min потерь) и приравнять к нулю, то:
Е![]() сли
в частном случае:
сли
в частном случае:
![]() ;
;
![]() .
.
Т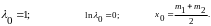 о
приходим к старому решению:
о
приходим к старому решению:
