
Кинематика точки. задания и методические указания по их выполнению для студентов специальности 280705.62 «Пожарная безопасность». Айбиндер Ю.М., Фролов И.А
.pdf1
Министерство образования и науки РФ
Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования
«Воронежский государственный архитектурно-строительный университет»
КИНЕМАТИКА ТОЧКИ
Задания и методические указания по их выполнению для студентов специальности 280705.62
« Пожарная безопасность»
Воронеж 2014
2
УДК 531.1(07)
ББК 22.21 + 22.211.я7
Составители: Ю. М. Айбиндер, И. А. Фролов, В. А. Муравьёв
Кинематика точки: задания и методические указания по их выполнению для студентов специальности 280705.62 «Пожарная безопасность». /Воронежский ГАСУ; сост.: Ю. М. Айбиндер, И. А. Фролов, В. А. Муравьёв. –
Воронеж, 2014. – 26 с.
Приводится описание индивидуальных заданий для выполнения аудиторных и самостоятельных работ по разделу «Кинематические способы задания движения точки» курса теоретической механики. Даются рекомендации по выполнению заданий и пример расчёта.
Предназначены для студентов специальности 280705.62 «Пожарная безопасность».
Ил.16. Табл. 4. Библиогр.: 7 назв.
УДК 531.1(07) ББК 22.21 + 22.211.я7
Печатается по решению научно-методического совета Воронежского ГАСУ.
Рецензент - Ю. И. Калинин, к.т.н., доц. кафедры строительных машин и инженерной механики Воронежского ГАСУ
3
Введение
Полный курс теоретической механики содержит три раздела: «Статика», «Кинематика» и «Динамика». Данные методические указания предназначены для студентов специальности 280705.62 «Пожарная безопасность» при их самостоятельной и аудиторной работах и проверке практических навыков при изучении раздела «Кинематика точки».
При работе над изучением раздела курса студент получает индивидуальное задание, для выполнения которого он должен знать:
а) понятие о системах координат (прямоугольных, естественных; векторных);
б) понятие о траектории, скорости, ускорении, радиусе кривизны траектории;
в) разделы элементарной геометрии и тригонометрии, связанные с решением треугольников с применением тригонометрических функций;
г) правила дифференцирования функций - находить их первую и вторую производные.
Вметодические указания включены:
1)основные понятия по курсу «Теоретическая механика» (кинематика точки);
2)условия задания схем механизмов;
3)рекомендации по выполнению индивидуального задания;
4)пример выполнения задания;
5)библиографический список литературы, необходимой для выполнения данного задания.
1.Краткие теоретические сведения
1.1.Основные понятия кинематики точки
Кинематикой называется раздел механики, в котором изучается движение материальных тел в пространстве с геометрической точки зрения, вне связи с силами, определяющими это движение.
4
Слово «кинематика» происходит от греческого слова «кинема», что значит движение. За единицу измерения расстояния принят метр - длина пути, проходимого светом в вакууме за 1/299792458 долю секунды.
За единицу времени (секунда) принята продолжительность 9192631770 периодов излучения, соответствующего переходу между двумя сверхтонкими уровнями основного состояния атома цезия Cs-133.
Изучение движения точки заключается в определении основных характеристик этого движения: положения точки в выбранной системе отсчёта, её скорости и ускорения в любой момент времени. Эта задача решается различными способами.
1.2. Кинематические способы задания движения точки
Существуют три способа задания движения точки: координатный, векторный и естественный.
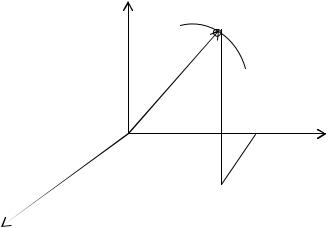
А. В координатной (прямоугольной) декартовой системе начало координат выбирают в неподвижной точке О, через которую проводят три взаимно перпендикулярные оси (рис.1).
Z
M(x;y;z)
z
O
y |
Y |
x
X
Рис.1. Декартова (прямоугольная) система координат
Любую из них можно выбрать за ось ОХ, тогда остальные выбирают против хода часовой стрелки (ОУ, OZ).

5
В этой системе координаты движущейся точки изменяются с течением времени, т. е они являются непрерывными функциями времени.
х
(1)
Эти уравнения определяют движение точки. Подставив в уравнение (1) значение времени t, получим координаты точки x, y и z. Они и определяют её положение.
Эти уравнения являются параметрическими уравнениями траектории точки. По ним легко определить уравнение траектории точки в декартовых координатах, исключив из уравнений время t, используя известные математические приёмы.
Б. При векторном способе задания движения точки её положение в про-
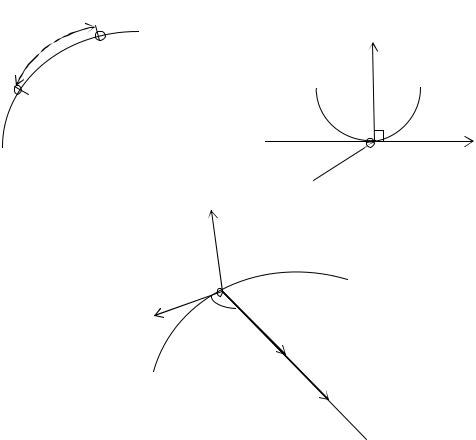
странстве однозначно определяется заданием радиуса-вектора , проведённого из некоторого неподвижного центра О в данную точку М (рис. 2)
М3 |
|
М |
|
М2 |
S |
||
|
|||
О |
+ |
|
∆
М1
М
О |
О |
∆
ср
∆
а) б)
Рис. 2. Векторный способ задания движения точки (а) и правило определения вектора истинной скорости (б)
Для определения движения точки нужно знать, как изменяется с течением времени радиус-вектор , т. е должна быть задана векторная функция аргумента t:
(2)
Траектория точки является геометрическим местом концов радиусавек- тора движущейся точки (годограф её радиус-вектора ).
Векторный способ задания движения материальной точки широко используется и в кинематике и динамике, т.к. он значительно упрощает многие выводы и иногда подчёркивает физическую сущность явлений.
6
От векторных формул легко перейти к аналитическим выражениям, обычно более удобным для вычисления.
В. При естественной системе отсчёта необходимы знания траектории движения точки. Эта система считается подвижной, т.к. за начало отсчёта принимается сама точка, движение которой исследуется.
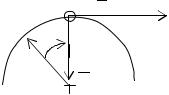
Положение точки на траектории определяют расстоянием , измеряемым по траектории и взятым с соответствующим знаком (рис.3, а, б).
М а) |
б) |
+ S |
n |
О
τ
М
в)
М
τ
n
K
Рис. 3. Схема естественной системы отсчета: положение точки М на траектории (а), положение осей системы координат отсчета (б, в)
Через исследуемую точку проводятся три взаимно перпендикулярные оси, одна из которых направлена по касательной ( к траектории в этой точке (М ); другая - ей перпендикулярна и направлена к центру по радиусу кривизны траектории в данной точке и называется главной нормалью (Мn), а третья - перпендикулярна им и называется бинормалью (Мв) (рис. 3, б, в).
7
1.3. Траектория, скорость, ускорение, движение точки
Траектория движения точки – это след, который оставляет она при своём перемещении. Траектория не зависит от времени. По своему характеру траектория может быть прямолинейной и криволинейной. Расстояние, которое проходит данная точка по траектории за фиксированный промежуток времени, – это её путь.
Уравнения движения точки однозначно определяют её положение в пространстве (и как частный случай – на плоскости) в зависимости от времени. Ранее было упомянуто, что существует три способа задания движения точки: координатный, векторный и естественный.
Движение точки может быть равномерным и неравномерным (равноускоренным и равнозамедленным).
Скорость движения точки – величина векторная. Она характеризует быстроту и направление её движения в данной системе отсчёта и в данный момент времени.
Из курса высшей математики известно, что скорость – это первая производная пути по времени, а ускорение – вторая производная, т. е.
v , ; |
,, |
или |
, |
(3) |
Следует помнить, что вектор скорости точки всегда направлен по касательной к траектории в рассматриваемый момент времени,в сторону движения.
1.4.Круговое движение точки
Случай равномерного криволинейного (кругового) движения точки М представлен на рис. 4.
М
R
н
Рис. 4. Равномерное круговое движение точки

8
При равномерном криволинейном (круговом) движении точки М вектор ее ускорения перпендикулярен к окружной (линейной) скорости и направлен к центру по радиусу кривизны (окружности):
Центростремительноен |
|
|
|
|
|
|
|
|
|
|
. |
(4) |
|
|
|
|
|
|
|
|
|
|
|||
ускорение |
|
|
направлено перпендикулярно век- |
|||||||||
|
н |
|||||||||||
тору линейной (окружной) скорости: |
|
|
||||||||||
|
|
|
|
|
; |
|
= 0 |
(5) |
||||
|
|
|
||||||||||
|
|
|
|
|
|
|
||||||
Случай равнопеременного криволинейногон |
движения представлен на |
|||||||||||
рис. 5.
М 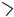
н
Рис. 5. Равнопеременное криволинейное движение
В этом случае скорость изменяется как по направлению, так и по вели-
чине:
,, |
. |
(6) |
Это ускорение называется касательным или тангенциальным. Оно определяет изменение скорости «по величине».
М 
н
Рис. 6. Полное ускорение при криволинейном движении.
Полное ускорение при криволинейном неравномерном движении равно геометрической сумме нормального и тангенциального ускорений.
9
= н |
|
; или |
|
|
; |
(7) |
|
|
|
|
|
, |
|
(8) |
|
|
|
|
|
|
|||
где ρ - радиус кривизны траектории; в случае движения точки по окружности
ρ= R.
1.5.Частные случаи движения точки
1.5.1.Прямолинейное равномерное движение (рис.7):
|
М |
V=const |
На рис.7. ρ – радиус кривизны. |
|
||||||||
|
=ρ∞ |
|
|
|
0; |
н |
0; |
|
|
|
=0 |
(9) |
|
|
= 0 |
||||||||||
Рис. 7. Прямолинейное равномерное |
|
н |
|
|
|
|
|
|||||
движение точки
1.5.2. Прямолинейное неравномерное движение (рис.8)
МV=f(t)
ρ=∞
Рис. 8. Прямолинейное и неравномерное движение точки
Поскольку траектория - прямая линия, то ρ=∞, значит, н=0. В этом случае скорость меняется только по величине и существует только касательное ускорение:
; (10)

10
1.5.3. Точка движется по криволинейной траектории равномерно (рис. 9)
|
V=f(t) |
Скорость изменяется лишь по направлению, V=const . |
|
||
|
|
Существует только нормальное (центростремительное) |
ускорение, т.к. ′ =0,
ρ
; |
(11) |
Рис.9. Равномерное криволинейное движение точки.
1.5.4. Точка движется по криволинейной траектории неравномерно
В этом случае: |
V=f(t); |
V=f(t)
М0
ρ |
|
; |
|
|
; |
(12) |
|
|
|
||||||
; |
|
2 |
2 |
; |
|
||
Рис.10. Неравномерное криволинейное движение точки
Результаты сведем в табл. 1.
1.6. Векторы скорости и ускорения точки
Величина скорости в координатной форме задания движения определяется через её проекции на оси координат ( см. рис. 3).
,
(13)
модуль скорости
