
Учебное пособие 2026
.pdfсигналом на выходе тракта промежуточной частоты или видеосигналом на выходе «преобразователя на нулевую частоту» - DOWN-конвертера.
= |
В устройстве цифровой обработки сигнала на выходе |
|||||||
( ) |
|
в |
= |
|
д |
|
||
АЦП |
он преобразуется |
последовательность отсчетов |
||||||
|
|
в моменты времени |
|
|
( – номер отсчета, – |
|||
интервал дискретизации). Частота дискретизации |
|
, равная |
||||||
|
|
|
д = 1/ |
, |
|
|
(3.1) |
|
определяется решаемой задачей. |
|
|
|
|
||||
|
Если необходимо восстановить исходный сигнал |
|||||||
по последовательности отсчетов |
, то частота |
выбирается( в) |
||||||
соответствии с теоремой Котельникова (Найквистад ) равной уд- |
||||||||
военной ширине спектра Ш исходного сигнала, а на практике |
||||||||
|
|
д |
= (2 |
÷ 3)Ш. |
|
|
(3.2) |
|
В других задачах цифровой обработки сигналов условие (3.2) может нарушаться.
Отсчеты квантуются по уровню и выдаются на выход
АЦП в виде двоичного - разрядного кода. |
|
|
Низкочастотный информационный сигнал |
(рече- |
|
вой, телевизионный видеосигнал) обычно рассматривается( ) |
как |
|
случайный процесс с соответствующими вероятностными, корреляционными и спектральными характеристиками.
Удобной моделью такого сигнала является нормальный (гауссовский) случайный процесс [7]. В простейшем случае это «белый шум» с некоррелированными соседними значениями и бесконечной равномерной спектральной плотностью, при этом при любой частоте дискретизации соседние отсчеты
независимы. Пример реализации последовательности отсчетов |
|||
единицах) |
|
= 1024 |
30 |
показан на рис. 3. а ( |
– номер отсчета). Спектр амплитуд реа- |
||
лизации из |
|
отсчетов этого сигнала (в условных |
|
|
показан на рис. 3.1б. |
||

После прохождения «белого шума» через фильтр нижних частот первого порядка отсчеты становятся коррелированными (шум становится «цветным»), соответствующая временная реализация показана на рис. 3.2а, а ее спектр – на рис. 3.2б, точками отмечены дискретные значения сигнала.
Рис. 3.1
Рис. 3.2
Как видно из рис. 3.2б, спектр сигнала остается неограниченным. Теорема Котельникова применима к сигналу с ограниченным (финитным) спектром, как показано на рис. 3.3б, его временная диаграмма приведена на рис. 3.3а. Удаление высших гармоник существенно сглаживает сигнал.
31

|
|
|
|
|
|
Рис. 3.3 |
|
|
|
|
|
|
|
Высокочастотный |
узкополосный |
аналоговый |
сигнал |
||||||
|
|
например, на выходе тракта промежуточной частоты |
|||||||||
приемника( ) ( |
) можно записать в виде |
+ |
( )), |
|
|
|
|||||
|
|
|
|
( ) = |
( )cos (2 |
|
|
(3.3) |
|||
где |
|
и |
|
– медленно меняющиеся амплитуда и началь- |
|||||||
ная фаза( ) сигнала( ) , определяемые модулирующим сигналом и |
|||||||||||
помехами, |
|
– несущая (центральная) частота. Его можно |
|||||||||
представить суммой квадратурных составляющих |
|
|
|||||||||
( ) |
|
( ) = ( ) cos(2 |
) + |
( )sin (2 |
), |
(3.4) |
|||||
и |
( ) |
– медленно меняющиеся амплитуды синфазной и |
|||||||||
|
|
|
|||||||||
квадратурной составляющих соответственно. |
|
|
|
||||||||
|
|
Сигнал с помощью АЦП дискретизируется по времени |
|||||||||
с частотой |
|
и квантуется по уровню |
- разрядным двоич- |
||||||||
ным кодом (дчисло уровней квантования равно |
|
= и2 |
). При- |
||||||||
меры дискретизации сигнала с частотами |
|
|
|
||||||||
|
|
|
|
|
|
|
|
3.4а и рис. 3.4б со- |
|||
(значение близко к (3.2)) показаны на рис.д = 10 |
|
д = 4 |
|||||||||
ответственно.
32
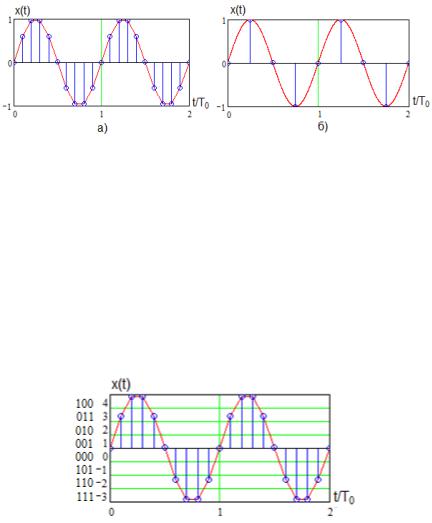
Рис. 3.4
При квантовании по уровню дискретные значения сигнала представляются двоичными кодами которые можно заменить их десятичными эквивалентами (возможны различные
варианты), как показано на рис. 3.5 при |
|
( |
|
уровней |
|
квантования). С ростом |
повышается |
точность оценки от- |
|||
= 3 |
|
= 8 |
|
||
счетов и динамический диапазон их представления. Напри-
мер, при |
|
отсчеты сигнала могут представляться шес- |
|||||
|
двоичным кодом ( |
|
уровней кванто- |
||||
тиразрядным= 16 |
|
|
|
|
2 |
= 2 = |
|
1024 раз больших) значений. |
максимальных (в |
||||||
вания) от минимальных до |
|
= 2 = 64 |
|
|
|
||
Рис. 3.5
3.2.Ряд Фурье, отрицательные частоты
Втеории цепей широко используются спектральные представления сигналов.
33
|
Для периодического сигнала |
|
с периодом |
ком- |
||||||||
плексная амплитуда –й гармоники равна( ) |
|
|
||||||||||
моники= 2 / |
= |
|
∫ |
|
( ) |
|
, |
(3.5) |
||||
|
|
|
||||||||||
где |
|
– частота первой гармоники, частота -й гар- |
||||||||||
|
равна |
|
|
|
|
= |
|
, |
|
(3.6) |
||
|
|
|
|
|
|
|
|
|
||||
- произвольный момент начала интегрирования, а |
|
|
||||||||||
показа- |
||||||||||||
– мнимая единица. Величину |
можно представить в = √ 1 |
|||||||||||
тельной форме в виде |
|
|
|
|
= |
|
|
|
|
|
||
|
= |
|
|
|
|
|
|
, |
|
(3.7) |
||
где |
– амплитуда, а |
Ψ = |
|
– соответственно |
||||||||
|
|
|
|
|||||||||
начальная фаза -й гармоники. |
|
|
|
|
|
|||||||
|
Ряд Фурье в комплексной форме имеет вид |
|
|
|||||||||
|
|
( ) = |
|
|
∑ |
|
|
. |
(3.8) |
|||
|
|
|
|
|
|
|||||||
Как видно, в (3.6) номера гармоник принимают поло-
жительные и отрицательные значения, тогда формально
удобно рассматривать гармоники с частотами (3.6) |
и |
. |
|||||||||||
Их сумма из (3.6) с учетом (3.7) определяет -ю гармонику |
|||||||||||||
= |
1 |
+ |
|
+( |
|
= |
= |
( |
+ Ψ ) |
|
|
||
|
2 |
|
) |
. |
(3.9) |
||||||||
|
|
|
|
|
|
|
|
||||||
Согласно (3.5) |
имеет место равенство |
|
|
|
|
|
|||||||
|
|
|
= = |
|
, |
|
|
|
|
|
(3.10) |
||
34
где – величина, комплексно сопряженная с . Тогда
спектр амплитуд является четной функцией номера (частоты) гармоники, а спектр фаз – нечетной функцией,
= |
, |
(3.11) |
Ψ = |
Ψ . |
(3.12) |
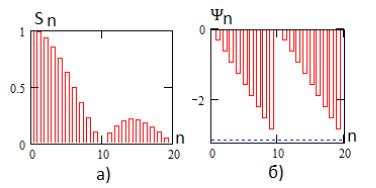
Традиционная (физическая) форма представления спектров амплитуд и фаз последовательности прямоугольных импульсов со скважностью 10 с положительными номерами (частотами) гармоник показана на рис. 3.6а и рис. 3.6б соответственно.
Рис. 3.6
При обработке дискретизированных сигналов удобно использовать представление спектров сигналов в области номеров (частот) гармоник от минус до плюс бесконечности, при этом согласно (3.7) амплитуды гармоник уменьшаются в два раза. Пример таких спектров показан на рис. 3.7.
35

Рис. 3.7
3.3. Спектры дискретизированных сигналов
На рис. 3.8 условно показаны физический (рис. 3.8а) и условный (с отрицательными частотами, рис. 3.8б) ограниченные по частоте спектры амплитуд низкочастотного аналогового видеосигнала, – ширина спектра.
|
|
|
Рис. 3.8 |
|
|
При дискретизации сигнала с частотой |
|
||
|
Ш = |
|
д > 2 |
(3.13) |
по |
|
|
|
|
в соответствии с теоремой Котельникова (3.2), ширина спек- |
||||
тра |
|
возникает периодическое «размножение» спектра |
||
|
частоте с периодом |
как в положительном, так и в отр и- |
||
цательном направленияхд |
оси частот, как показано на рис. 3.9а |
|||
36

при |
д = 4 |
. |
|
|
|
||
|
На рис. 3.9б показан предельный случай выбора часто- |
||
ты дискретизации из (3.13) при |
д= 2 . |
||
Рис. 3.9
При нарушении (3.13) спектры на рис. 3.9 перекрываются, что приводит к искажениям сигнала при его цифровой
обработке. |
д/2 |
|
д/2 |
|
На практике при (3.13) представляет интерес интервал |
||||
частот от |
|
до |
|
. Но если производится какое-либо |
преобразование частоты дискретизированного сигнала, прореживание отсчетов или их интерполяция, то размножившиеся спектральные компоненты на рис. 3.9 трансформируются в область рабочих частот, что необходимо учитывать при цифровой обработке сигналов. То же относится и к помехам на аналоговом входе в окрестности частоты дискретизации.
При дискретизации аналоговых узкополосных (модулированных) радиосигналов, спектр которых имеет вид рис. 3.12, также наблюдается размножение спектров, как показано
на рис. 3.13 при |
д = 4 |
|
|
(3.14) |
( ‒ несущая частота, F – ширина спектра модулирующего сигнала, 2 F – полоса частот радиосигнала).
37
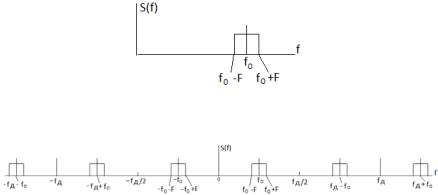
Рис. 3.10
Рис. 3.11
Ш = + |
|
|
|
|
|
|
|
Полная ширина спектра узкополосного сигнала равна |
|||||||
, тогда в соответствии с теоремой Котельникова |
|||||||
(3.2) |
|
д 2( |
+ ), |
|
|
|
|
в соответствии =с |
10 |
|
|
(3.15) |
|||
|
= 1 |
|
|
|
. На- |
||
при этом занимаемая сигналом полоса частот равна |
|
||||||
пример, при |
|
МГц и |
|
МГц частота |
дискретизации |
||
|
|
|
2 |
|
|||
(3.2) должна быть не менее 24 МГц.
Однако можно использовать и частоты дискретизации,
значительно меньшие границы (3.15). Например, если выбрать |
||
д = |
/2, |
(3.16) |
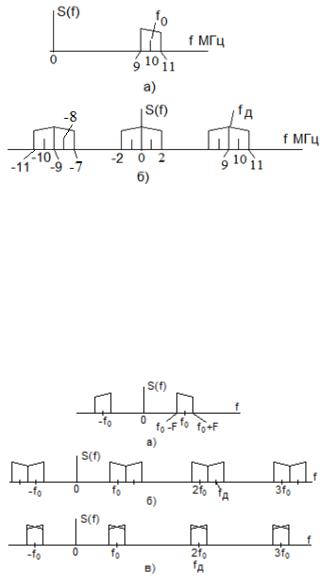
то для аналогового сигнала со спектром на рис. 3.12а спектр дискретизированного сигналад = 9 примет вид, показанный на рис. 3.12б. Как видно, при МГц возникает перенос спектра
узкополосного сигнала в область нижних частот. Подобные результатыд можно получить и при других (не любых) значениях , однако предельной границей частоты дискретизации узкополосных сигналов вида рис. 3.10 является величина
38
д = 4 . |
(3.17) |
|
Рис. 3.12
При выборе частоты дискретизации на границе (3.15) |
|
д = 2( + ), |
(3.18) |
спектр сигнала (рис. 3.13а) после дискретизации будет иметь вид, показанный на рис. 3.13б.
Рис. 3.13
39
