Учебное пособие 2026

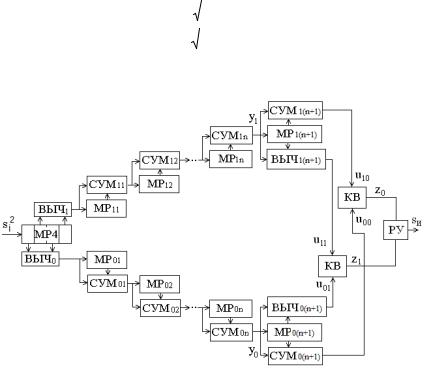
В квадратичных преобразователях КВ вычисляются

Рис. 8.9

Решение о переданном символе принимается после поступления элемента сигнала с ОФТ по импульсам тактовой

синхронизации демодулятора: если z0 > z1 , то сдвиг фазы 0, а

иначе он равен π .

Зависимости z0 и z1 от номера текущего периода i представлены на рис. 8.10. Функция z0 показана сплошной линией, а z1 - пунктиром, а прямоугольными импульсами отмечено изменение начальной фазы ϕ . В начале наблюдается переходной процесс заполнения регистров сдвига.

100

Рис. 8.10

Как видно, если сдвиг фаз между колебаниями принимаемого и предшествующего элементов равен π , то максимума по завершении приема элемента достигает величина z1 ,

при этом z0 = 0. Если фазы этих элементов одинаковы, то максимум имеет место в канале z0 , а z1 = 0. Таким образом,

решение о принятом информационном символе принимается по наибольшему значению z0 или z1 .

Неравенство z0 > z1 при подстановке (8.12) – (8.14) можно записать в виде: при

принимается решение о сдвиге фазы 0, а иначе – π . Соответствующая (8.15) структурная схема демодулятора показана на рис. 8.11.

На рис. 8.12 сплошной линией показана зависимость нормированных значений zi /2N (8.15) от номера текущего

периода i/N без помех при N = 256, пунктиром показано изменение фазы сигнала. В моменты формирования решения результат аналогичен показанному на рис. 8.10.

101

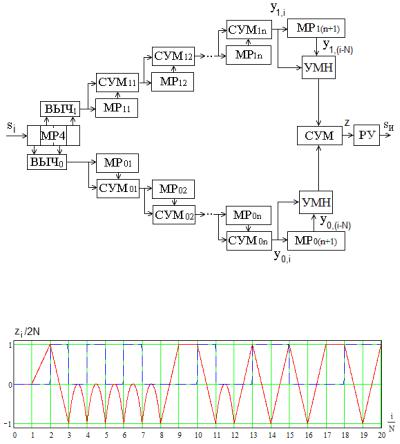
Рис. 8.11

Рис. 8.12

8.4. Некогерентный демодулятор четырехпозиционного сигнала с ОФМ

У сигнала с четырехпозиционной ОФМ сдвиг фаз между соседними символами может принимать значения 0 , π / 2, π и 3π / 2 . Структурная схема демодулятора показана на рис. 8.13.

102

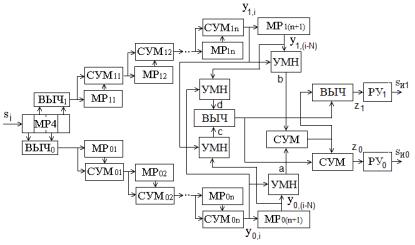
Рис. 8.13

По показанным на рис. 8.13 величинам y0,i , y1,i и за-

по которым в решающих устройствах РУ0 и РУ1 (компарато-

103

рах) принимаются решения о значениях принимаемых четырехпозиционных информационных символов sИ со значения-

ми 00, 01, 10, 11.

При отсутствии шума по окончании информационного символа y0,i , y1,i принимают значения

идалее

z0 = a+b+c−d = (2NS)2 cos(a π /2)+(2NS)2 sin(a π /2),(8.22)z1 = a+b−c+ d = (2NS)2 cos(a π /2)−(2NS)2 sin(a π /2).

104

По окончании приема символа величины z0 и z1 не

зависят от начальной фазы сигнала и равны ±(2NS)2 при всех значениях информационных символов.

На рис. 8.14 представлены зависимости от номера i/N принятого периода сигнала нормированных откликов z0 и z1

на входе решающих устройств при отсутствии шума и

N = 256.

Рис. 8.14

Пунктиром показаны изменения фаз элементов сигна-

ла, деленных на 2π . При целочисленных i/N принимаются решения

105

9. ЦИФРОВЫЕ ИЗМЕРИТЕЛИ

9.1. Интегратор

Цифровой интегратор выполняет операцию численного интегрирования сигнала (функции) s(t) на заданном времен-

ном инетервале TИНТ от t −TИНТ до текущего значения t,

t−TИНТ

Эти устройства применяется в различных устройствах управления и обработки сигналов.

Интервал интегрирования TИНТ разбивается на N −1 отрезков с шагом ∆,

N = 2n , n ‒ целое число.

На интервале TИНТ в моменты ti = ∆ i с помощью АЦП формируются дискретные отсчеты si = s(ti ), i - номер

отсчета, по которой численно определяется интеграл (9.1). Применяются [118, 119] разнообразные методы вычисления определенного интеграла:

‒ прямоугольников

106

и другие.

Метод парабол (Симпсона) обеспечивает наименьшую

погрешность при заданном числе интервалов N −1, которое в простых вычислениях обычно выбирается от 30 до 50. Общим свойством рассмотренных методов является снижение по-

грешности с ростом N , особенно при N >>1000, однако при этом возникают вычислительные трудности и необходимо использовать быстрые цифровые алгоритмы.

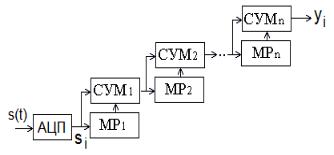
Наиболее прост интегратор на основе по формулы прямоугольников (9.3), структурная схема интегратора показана на рис. 9.1.

Рис. 9.1

107

Рассмотрим интегрирование гармонического сигнала с единичной амплитудой и частотой F вида

= sin(2πFt)−sin(2πF(t −TИНТ )).

На рис. 9.2 показаны результаты имитационного моделирования работы интегратора методом прямоугольников при

F =1000Гц, N = 2048 (n =11), частоте дискретизации АЦП fКВ =1МГц (∆ =1мкс) длительности интервала интегрирования TИНТ = 2,048мс. На рис. 9.2а сплошной линией показан результат интегрирования F(t) (9.3), а точечной – его точное значение F0(t) (9.7). В начале в течение TИНТ возникает переходной процесс заполнения регистров сдвига, а затем F(t) практически совпадает с F0(t) (рис. 9.2б), график погрешности F(t)− F0(t) показан на рис. 9.2в (менее 0,5%).

Рис. 9.2

Цифровой интегратор (рис. 9.1) для обеспечения малой погрешности требует, чтобы частота дискретизации была много больше частоты сигнала.

108

Значительно лучшие результаты обеспечивает интегратор на основе метода Симпсона. Структурная схема интегратора показана на рис. 9.3. Входной сигнал x(t), поступает на

вход АЦП, который в моменты времени ti , определяемые

ГТИ 3 ( i – порядковый номер), с интервалом времени τ формирует отсчеты xi входного сигнала. В текущий момент ti ,

k > N, обрабатывается (интегрируется) выборка отсчетов объемом

N = 2m+2 +1 (9.8)

(m – целое число). Выбор N (9.8) необходим для организации быстрой вычислительной процедуры в каналах накопления отсчетов КНО0 и КНО1.

Значение интеграла на интервале времени от ti −(N −1)τ до ti вычисляется по формуле парабол (9.5) в со-

ответствии с выражением

Структурная схема интегратора показана на рис. 9.3.

109