
Учебное пособие 1850
.pdf
x
x
1 |
|
|
|
Vz |
|
|
|
Vy |
; |
||
2 |
|
|
|
y |
|
|
|
z |
|||
|
|
|
|
|
|
|
|
||||
|
1 |
|
|
Vz |
|
|
|
Vy |
|
; |
|
2 |
|
|
y |
|
|
|
z |
|
|||
|
|
|
|
|
|
|
|||||
y
y
1 |
|
|
|
Vx |
|
|
|
Vz |
|
; |
|
2 |
|
|
|
z |
|
x |
|||||
|
|
|
|
|
|||||||
|
1 |
|
|
Vx |
|
|
Vz |
; |
|||
2 |
|
|
z |
|
x |
||||||
|
|
|
|
||||||||
x
z
1 |
|
|
|
Vy |
|
|
V |
x |
; |
|||
2 |
|
|
|
x |
|
y |
||||||
|
|
|
|
|
|
|||||||
1 |
|
|
Vy |
|
V |
x |
. |
|||||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
x |
|
|
y |
||||||
предыдущую формулу и аналогичные ей можно записать в виде:
Vx C Vx |
Vx |
|
x |
z y |
y z |
y z |
y y ; |
|
|||
x |
|
||||||||||
|
|
|
|
|
|
|
|
|
|||
Vy C Vy |
Vy |
y |
z z |
z x |
z x |
x z ; |
|
||||
|
|
|
|
||||||||
y |
|
||||||||||
|
|
|
|
|
|
|
|
|
|||
Vz C Vz |
|
|
Vz |
|
z |
y x |
x y |
x y |
y x . |
|
|
|
|
z |
|
||||||||
|
|
|
|
|
|
|
|
|
|||
Выясним физический смысл отдельных слагаемых, |
|||||||||||
входящих в систему уравнений. |
|
|
|
|
|
||||||
Члены |
|
|
Vx x , Vy y , |
Vz z |
|
определяют |
|||||
составляющие |
скорости |
|
относительной |
деформации |
|||||||
растяжения или сжатия вдоль осей координат. |
|
|
|
||||||||
Действительно, |
длина |
грани |
параллелепипеда |
x |
|||||||
направленной вдоль оси ox, вследствие разности скоростей на
ее концах за секунду изменится на величину Vx |
x |
x . |
Разделив это выражение на длину грани |
x , |
получим |
скорость относительной продольной деформации вдоль оси ОХ. Аналогично происходит деформация вдоль осей ОУ и OZ.
Члены x , y , z есть величины, пропорциональные
составляющим скорости угловых деформаций двугранных углов параллелепипеда.
Действительно, рассмотрим одну грань параллелепипеда в плоскости УОХ (рис. 1.4).
21

.
. .
Рис. 1.4 |
Рис. 1.5. |
Вследствие разности скоростей угловых точек грань АВ |
|
прямоугольника ABFE за время |
t повернется на угол |
(положение АВ'), грань АЕ — на угол  (положение АЕ'), точка
(положение АЕ'), точка
F переместится в точку F'. Таким образом, прямоугольник ABFE деформируется и превратится в параллелограмм AB'F'E', при этом грани АВ и FE повернутся против часовой стрелки с угловой скоростью Vy x , а грани BF и АЕ — по часовой
стрелке с угловой скоростью |
Vx |
y . |
Сумма Vx y Vy |
x |
характеризует составляющую |
скорости угловой деформации относительно оси OZ. Аналогично можно рассмотреть две другие грани параллелепипеда и определить две составляющие скорости угловой деформации параллелепипеда относительно осей ОХ и ОУ.
Полусуммы, обозначенные через x , y , z ,
характеризуют скорость относительного сдвига каждой пары параллельных граней параллелепипеда.
Члены x , y , z являются составляющими вектора угловой скорости вращения .
22
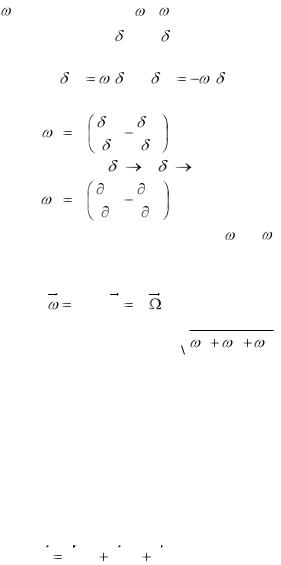
Допустим, что жидкость вращается вокруг оси ОУ с угловой скоростью y , а величины Vy, x , y равны нулю.
В этом случае проекции скоростей Vx и Vz в точке A (рис. 1.5), расположенной на малом расстоянии от осей координат,
определяются равенствами: Vx |
y |
z и |
Vz |
y |
x , |
|||||||||
откуда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
Vx |
|
|
|
Vz |
. |
|
|
||
y |
|
|
|
|
|
|
|
|
|
|||||
2 |
|
|
z |
|
|
x |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
||||
В предельном случае, когда |
x |
0, |
|
|
z |
0, |
|
|||||||
|
|
1 |
|
|
Vx |
|
|
Vz |
. |
|
|
|||
y |
|
|
|
|
|
|
|
|
|
|||||
2 |
|
|
z |
|
|
x |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
||||
Аналогично можно получить выражения для |
x и z . |
|||||||||||||
Угловую скорость вращения в векторной форме можно записать в виде
1 |
rotV |
1 |
. |
|
2 |
2 |
|||
|
|
Модуль вектора угловой скорости 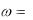

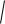
2 |
2 |
2 . |
x |
y |
z |
Следует отметить, что поступательное, вращательное движение и деформация элемента жидкости происходят одновременно независимо друг от друга.
Таким образом, в полученной системе уравнений слагаемые Vx, Vv, Vz являются компонентами поступательной скорости, суммы в квадратных скобках — компонентами скорости деформации, в круглых скобках — компонентами вращательной скорости.
В векторной форме выражение для скорости жидкого элемента имеет вид
V V пост V деф V вр
Теорема Коши — Гольмгольца о разложении жидкого элемента является видоизменением известной теоремы Даламбера для твердого тела, однако она справедлива лишь для бесконечно малой жидкой частицы, так как разложение имеет
23
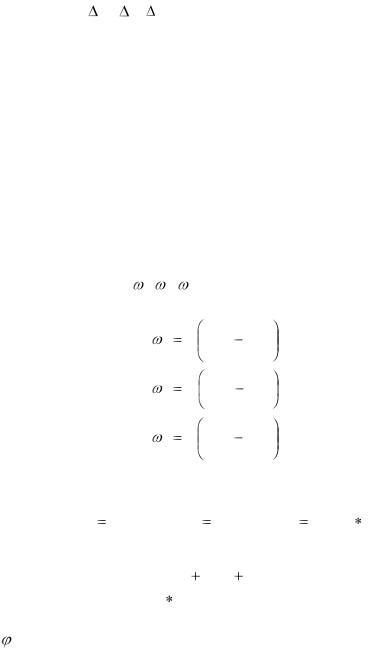
место только для частицы в точке С, находящейся на малом расстоянии ( x :, y , z ) от точки А.
Частный случай движения, когда частицы не вращаются вокруг мгновенных осей, называется безвихревым или
потенциальным.
2. ПОТЕНЦИАЛЬНОЕ И ВИХРЕВОЕ ДВИЖЕНИЕ ЖИДКОСТЕЙ И ГАЗОВ
2.1.Потенциал скорости
Для большинства задач аэродинамики весьма важным является изучение потенциального движения.
Потенциальным движением жидкости называется безвихревое движение, т.е. такое движение, в котором компоненты вихря x , y , z равны нулю.
Из теоретической механики известно, что
|
|
1 |
|
dV |
|
|
dVy |
; |
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
2 |
|
dz |
|
|
dy |
|
|
|
|
|
|
|
|
|||
|
|
1 |
|
dVx |
|
|
dVz |
; |
y |
2 |
|
dx |
|
dz |
|||
|
|
|
|
|||||
|
|
|
|
|
|
|||
|
|
1 |
|
dVy |
|
|
dV |
|
|
|
|
|
|
|
|
x |
. |
z |
2 |
|
dy |
|
|
dx |
||
|
|
|
|
|||||
|
|
|
|
|
|
|||
Следовательно, для потенциального движения получаем соотношения
dV |
|
dVy |
|
dV |
|
dV |
dVy |
|
dV |
|
|
z |
|
|
; |
x |
|
z |
; |
|
|
x |
( ). |
|
|
|
|
|
|
|
|
||||
dz |
|
dy |
|
dx |
|
dz |
dy |
|
dx |
|
|
Рассмотрим дифференциальный трехчлен
Vx dx Vy dy Vz dz.
Выполнение условий ( ) говорит о том, что этот трехчлен является полным дифференциалом некоторой функции
(x, y, z) , т.е.
24

|
Vx dx Vy dy Vz dz |
|
|
(x, y, z). |
|
|
||||||||||
Функция (x, y, z) носит |
|
название |
|
потенциала |
скорости и |
|||||||||||
играет важную роль в аэродинамике. |
|
|
|
|
|
|
|
|||||||||
Так как d |
|
|
|
|
d |
|
|
|
d |
|
|
d |
|
то очевидно, |
||
(x, y, z) |
|
|
dx |
|
|
dy |
|
|
dz, |
|||||||
|
dx |
dy |
dz |
|||||||||||||
что |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Vx |
|
d |
; |
Vy |
|
d |
; |
|
Vz |
|
d |
. |
|
|||
|
|
|
|
|
|
|
|
|
||||||||
|
dx |
|
dy |
|
|
dz |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
т.е. проекция скорости на координатную ось равна частной производной от потенциала скорости по соответствующей координате. Это важное свойство потенциала скорости сохраняется и для произвольного направления. Наличие потенциала скорости дает возможность построить сравнительно простую теорию безвихревых течений.
2.2. Уравнение неразрывности для потенциального движения жидкости
В общем виде уравнение неразрывности имеет вид
d |
|
dV |
|
dVy |
|
dV |
0 |
|
|
x |
|
|
|
z |
|
|
|
|
|
|
|
||
dt |
|
dx |
|
dy |
|
dz |
|
Выражая проекции скорости через функцию тока, получаем, что
|
d |
|
d 2 |
|
d 2 |
|
|
d 2 |
|
0 |
|
|||||
|
dt |
dx2 |
dy2 |
dz2 |
|
|||||||||||
|
|
|
||||||||||||||
В случае, если жидкость |
|
несжимаемая, т.е |
const , |
|||||||||||||
уравнение неразрывности принимает вид |
|
|
||||||||||||||
|
|
|
d 2 |
|
|
d 2 |
|
|
d 2 |
|
0 |
|
|
|||
|
|
|
dx2 |
|
|
dy2 |
|
|
dz2 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Это уравнение носит название уравнения Лапласа, а функция , удовлетворяющая этому уравнению, – гармонической функции.
25

Уравнение Лапласа является линейным дифференциальным уравнением второго порядка в частных производных. Методы его решения достаточно хорошо изучены. Уравнение имеет бесчисленное множество решений.
Чтобы найти решение уравнения Лапласа при обтекании конкретного тела, вводятся граничные условия.
Пусть тело имеет поверхность, заданную уравнением f (x, y, z) 0 Это тело обтекается потоком, скорость которого в
бесконечности r |
параллельна оси Х и равна V . В этом |
||||
случае необходимо, чтобы при r |
,Vx |
V и Vy |
Vz 0. |
||
Предполагая, что поток безотрывно скользит по |
|||||
поверхности |
тела, имеем второе граничное условие: на |
||||
поверхности |
тела Vn |
0 , где Vn |
– |
проекция |
скорости на |
нормаль к поверхности тела.
2.3. Функция тока.
Для плоского течения несжимаемой жидкости уравнение неразрывности (Лапласа) имеет вид
dV |
|
dVy |
0 |
x |
|
|
|
dx |
|
dy |
|
Это уравнение удовлетворяется, если ввести функцию (x, y) , такую что
Vx |
d |
; |
|
|
Vy |
|
d |
. |
|
|
|
||
|
|
|
|
|
|
|
|
|
|||||
dy |
|
|
|
|
dx |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
Действительно, |
подставляя Vx |
и Vy |
в уравнение |
||||||||||
|
|
|
|
|
|
|
|
|
d 2 |
|
|
d 2 |
|
неразрывности, приходим к равенству: |
|
|
|
|
|
0 , из |
|||||||
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
dydx |
dxdy |
|||
которого следует тожество |
d 2 |
|
d 2 |
|
. |
|
|
|
|
|
|
||
dydx |
dxdy |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
||||
26
Таким образом, для всякого плоского потока жидкости существует некоторая функция , связанная с проекциями
скорости указанными соотношениями.
Можно показать, что эта функция сохраняет постоянное значение вдоль линии тока.
Действительно, уравнение линии тока для плоского потока имеет вид dx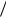 Vx dy
Vx dy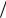 Vy , или Vy dx Vx dy 0 .
Vy , или Vy dx Vx dy 0 .
Подставляя вместо Vx |
и Vy |
их значения через функцию |
|||
, получаем: |
|
|
|
|
|
|
d |
dx |
|
d |
dy 0 |
|
|
|
|
||
|
dx |
|
dy |
||
Так как левая часть является полным дифференциалом функции  вдоль линии тока, то d
вдоль линии тока, то d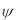 0 или
0 или 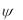 const вдоль линии тока.
const вдоль линии тока.
Благодаря этому свойству функцию  называют
называют
функцией тока.
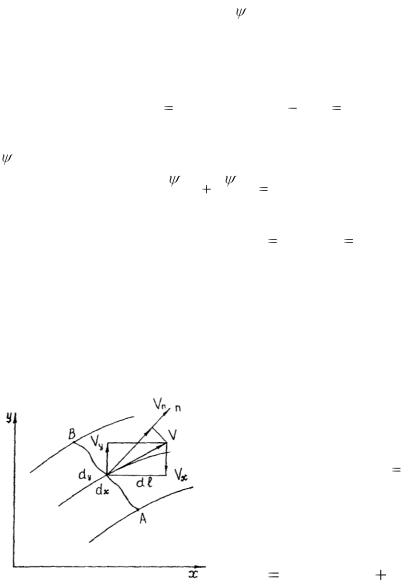
Функция тока имеет определенный физический смысл. Рассмотрим цилиндрическую поверхность единичной
высоты, опирающуюся на некоторый контур, соединяющий А и В (рис. 2.1).
|
Объемный |
расход |
||
жидкости |
через, |
элемент |
||
поверхности, |
имеющий в |
|||
основании |
элемент |
контура |
||
dl , |
равен |
dQ Vn dl . |
||
Нормальная |
составляющая |
|||
скорости Vn |
определяется по |
|||
|
|
|
|
формуле: |
Vn |
Vx cos(nx) |
Vy cos(ny) |
||
Рис. 2.1
А косинусы углов, образуемых нормалью с осями координат, равны
27
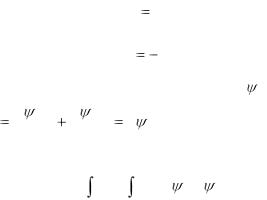
|
|
|
cos(nx) |
|
dy |
; |
|||
|
|
|
|
|
|
||||
|
|
|
|
|
|
dl |
|||
|
|
|
cos(ny) |
|
|
dx |
. |
||
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
dl |
||
Подставляя вместо Vx |
и Vy их выражения через получаем: |
||||||||
|
d |
d |
, |
|
|
|
|||
dQ |
|
dx |
|
dy d |
|
|
|
||
dx |
dy |
|
|
|
|||||
отсюда расход через кривую АВ равен
B B
QAB  dQ
dQ 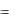 d
d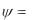 B
B 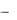 A
A
A A
Таким образом, объемный расход несжимаемой жидкости через произвольный отрезок кривой равен разности значений функции тока в конечных ее точках и не зависит от формы кривой.
Очевидно, что если точки А и В совпадают, то при однозначной функции тока 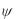 расход через замкнутую кривую
расход через замкнутую кривую
равен нулю.
Если кривая АВ является отрезком линии тока, то расход сквозь нее также равен нулю, так как вдоль линии тока функция тока равна постоянной величине.
Отсюда следует, что количество жидкости, протекающей в единицу времени между двумя произвольными линиями тока, есть постоянная, численно равная разности значений функции тока на этих линиях тока.
2.4.Циркуляция скорости
Ваэродинамике большую роль играет понятие о циркуляции скорости по заданному контуру.
Выделим в движущейся жидкости произвольный фиксированный в пространстве замкнутый контур С (рис. 2.2).
28
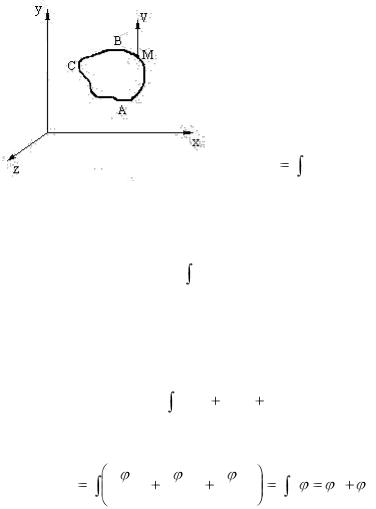
Пусть в некоторой его точке М скорость изображается вектором V . Составим произведение V cos(VdS)dS , где
dS – элементарная длина замкнутого контура. Возьмем от этого выражения интеграл по дуге АВ. Тогда будем иметь:
|
Г |
V cos(VdS)dS |
|
|
AB |
|
|
Рис. 2.2 |
Выражение |
Г |
называется |
циркуляцией скорости по дуге АВ.
Обычно циркуляция скорости вычисляется по всему замкнутому контуру С, т.е.
Г 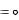 V cos(VdS)dS
V cos(VdS)dS
C
Направление интегрирования будем считать положительным, если охватываемая контуром область остается слева.
Учитывая, что под знаком интеграла стоит скалярное произведение векторов V и dS можно записать:
Г  (Vx dx Vy dy Vz dz)
(Vx dx Vy dy Vz dz)
C
В случае потенциального течения циркуляцию можно выразить через потенциал скорости, т.е.
Г |
d |
dx |
d |
dy |
d |
dz |
d |
|
A . |
|
|
|
|
B |
|||||||
dx |
dy |
dz |
||||||||
AB |
|
|
|
AB |
|
|
Это означает, что для потенциального течения циркуляция вдоль дуги АВ не зависит от формы дуги и равна разности значений потенциала скорости в конечных точках дуги. В случае когда точки А и В совпадают, т.е. контур замкнутый и функция  является однозначной функцией
является однозначной функцией
координат, циркуляция становится равной нулю.
29

2.5. Плоские потенциальные течения жидкости
Мы установили, что для потенциального плоского течения характерны две функции: потенциал скорости (x, y)
и функция тока |
(x, y) . |
|
|
|
|
|
|
|
|
|
|
|
|||
Составляющие скорости потока следующим образом |
|||||||||||||||
выражаются через эти функции: |
|
|
|
|
|
|
|||||||||
Vx |
d |
; Vx |
|
d |
; Vy |
d |
; Vy |
d |
. |
||||||
|
|
|
|
|
|
||||||||||
dx |
|
dy |
dy |
dy |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||
Из этих равенств следуют соотношения между |
|||||||||||||||
функциями и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d |
d |
|
d |
|
|
d |
|
|
||||
|
|
|
|
|
|
; |
|
|
|
|
|
. |
|
|
|
|
|
|
dx |
dy |
|
dy |
|
dy |
|
|
|||||
Эти соотношения носят название условий Коши-Римана и в теории функций комплексного переменного они выражают условие, что комплексная комбинация этих двух функций от двух действительных переменных, т.е. (x, y) i (x, y) ,
является аналитической функцией комплексного переменного
z x |
iy . |
|
|
|
|
|
|
|
|
|
|
Обозначим |
эту |
функцию |
через |
|
W |
т.е. |
|||
W(z) |
|
(x, y) i (x, y) . |
|
|
|
|
|
|
||
|
Функция W (z) |
носит |
название |
комплексного |
||||||
потенциала, или характеристической функции течения. |
|
|||||||||
|
Возьмем |
производную от комплексного |
потенциала |
|||||||
W |
i |
по |
комплексному |
переменному |
z |
x iy . |
Из |
|||
теории функций комплексного переменного следует, что эта производная имеет вид
dW |
|
d |
i |
d |
i |
d |
|
d |
. |
|
|
|
|
|
|
||||
dz |
|
dx |
|
dx |
|
dy |
|
dy |
|
Или, заменяя производные через проекции скорости, получаем:
30
