Учебное пособие 1830

Из условия симметрии следует, что линии магнитной индукции тороида представляют собой окружности и что во всех точках этой линии напряжённости одинаковы. Поэтому напряжённость Н можно вынести за знак интеграла, а интегрирование проводить в пределах от нуля до 2πr, где r- радиус окружности, совпадающей с линией индукции, вдоль которой вычисляется циркуляция, т.е.

2 r

H d H d 2 rH.

L0

Сдругой стороны, в соответствии с законом полного тока циркуляция вектора напряжённости магнитного поля равна сумме токов, охватываемых контуром, вдоль которого вычисляется циркуляция:

n

H d Ii .

L i 1

Приравняв правые части равенств этих выражений получим

n

2 rH Ii .

i 1

Линия, проходящая вдоль тороида, охватывает число токов, равное числу витков тороида. Сила тока во всех витках одинакова. Поэтому

2πrН = NI,

откуда

H NI . 2 r

С учетом радиуса средней линии r = (R1+ R2)/2= (d1+ d2)/4, получим

H 2NI .

(d1 d2 )

Магнитная индукция В0 в вакууме связана с напряжённостью поля соотношением В0=μ0Н. Следовательно,

19

Сколько витков N содержит обмотка на кольце, если при силе тока I = 4А индукция В магнитного поля в воздушном зазоре равна 0,5 Тл. Рассеянием магнитного потока в воздушном зазоре можно пренебречь. Явление гистерезиса не учитывать.

Решение

Пренебрегая рассеянием магнитного потока, мы можем принять, что индукция поля в воздушном зазоре равна индукции поля в чугуне. На основании закона полного тока запишем

IN = H + H0 0 .

По графику зависимости индукции от напряженности магнитного поля для ферромагнетиков (см. приложение) находим что при B = 0,5 Тл, напряжённость Н магнитного поля в чугуне равна 1,5 кА/м. Так как для воздуха μ = 1, то напряжённость поля в воздушном зазоре

H0 B 0 0,4 МА/м.

Искомое число витков

N = (H +H0 0) / I = 900.

20

2.КОЛЕБАНИЯ И ВОЛНЫ

2.1.Основные формулы

Механические колебания

Дифференциальное уравнение гармонических колебаний материальной точки и его решение

x 02x 0, x Acos( 0t 0),

где x – смещение колеблющейся точки от положения равновесия; А – амплитуда колебаний, т.е. максимальное смещение от положения равновесия; ω0 – собственная частота колебаний.

Уравнение траектории точки, участвующей в двух взаимно перпендикулярных колебаниях

Амплитуда и фаза результирующего колебания, возникающего при сложении двух одинаково направленных колебаний с одинаковыми частотами.

A2 = A12 + A22 + 2 A1 A2 cos ( 2 - 1),

Дифференциальное уравнение затухающих колебаний

иего решение

где =r/2m – коэффициент затухания; r – коэффициент сопротивления; 02 2 – угловая частота затухающих

колебаний; А = A0 e- t – амплитуда колебаний в момент времени t.

где А(t) и A(t+T) – амплитуды двух последовательных колебаний, отстоящих по времени друг от друга на период; Ne – число колебаний, в течение которых амплитуда уменьшается в е=2,73 раз.

Дифференциальное уравнение вынужденных колебаний и его решение для установившихся колебаний:

x 2 x 02x f0 cos вt,

x Acos( вt ),

где F0 cos ωв t - внешняя периодическая сила, действующая на

tg 2 в

02 в2

22

Резонансная частота и резонансная амплитуда

2.2.Электрические колебания

Дифференциальное уравнение собственных электрических колебаний в контуре и его решение

q 02q 0, q q0 cos( 0t ),

1

контура, 02 2 - частота затухающих колебаний.

Добротность контура

1 L

Q = R C

Закон сохранение энергии в идеальном колебательном контуре (LС-контур)

qm2 LIm2 = q 2 LI 2 const,

2C 2 2C 2

23

Дифференциальное уравнение вынужденных электрических колебаний при последовательном включении в контур переменного напряжения и его решение

q x 2 q 02q Um cos вt, L

q qm cos( вt ),

I Imcos( вt 1),

где - разность фаз между колебаниями заряда и внешней ЭДС; в - частота внешней ЭДС; Im=ωв qm – амплитуда тока,1 = - /2 – сдвиг по фазе между током и внешней ЭДС.

2.3.Волны

Уравнение плоской бегущей волны

где - смещение точки, имеющей координату x в момент времени t, k = 2 / - волновое число, υ – фазовая скорость,- длина волны.

24

Уравнение стоячей волны

(x,t) 2A0 coskx cos t,

Длина стоячей волны, т.е. расстояние между двумя соседними пучностями или двумя соседними узлами, и длина бегущей волны связаны соотношением:

ст = / 2

Скорость распространения в веществе:

а) упругой продольной волны

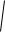E ,

где E – модуль Юнга, - плотность вещества.

б) упругой поперечной волны

G ,

где G – модуль сдвига,

в) упругой продольной волны в газах

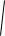RT ,

где = Сp /Cv – показатель адиабаты, - молярная масса.

г) электромагнитной волны

где , - диэлектрическая и магнитная проницаемости среды, с 3 108 м/с - скорость электромагнитных волн в вакууме.

25

Эффект Доплера для акустических волн

зв пр 0 ,

зв ист

где ν – частота звука, воспринимаемого движущимся приёмником, υзв - скорость звука, υпр – скорость приемника ( υпр > 0 , если приемник приближается к источнику), υист – скорость источника (υист > 0, если источник приближается), 0 - частота звука, испускаемого источником.

2.4. Примеры решения задач по колебаниям и волнам

Пример 1. Частица совершает гармонические колебания вдоль оси х около положения равновесия x=0, частота колебания 0=4с-1. В некоторый момент времени координата частицы x0 = 25 см и ее скорость 0х = 100 см/с. Найти координату x и скорость частицы через t = 2,4 с после этого момента.

Решение

Запишем уравнение гармонических колебаний частицы

в виде:

x = Acos( 0t + 0),

тогда уравнение проекции скорости на ось Ox будет иметь вид:

x x A 0 sin( 0t 0 ) .

Для нахождения параметров данных уравнений воспользуемся начальными условиями. При t = 0 имеем:

х0 = Аcos 0,

26

Координата и проекция скорости частицы х в момент времени t = 2,4 с

x= 35·cos(4·2,4 –π/4)=-28,8см,

x 35 4sin(4 2.4 /4) 79,6см/с.

Пример 2. Точка совершает гармонические колебания вдоль некоторой прямой с периодом Т = 0,6 с и амплитудой А = 10 см. Найти среднюю скорость точки за время, в течении которого она проходит путь А/2: а) из положения равновесия; б) из крайнего положения.

Решение

Выберем за начало отсчета времени момент, когда точка проходит положение равновесия. Тогда уравнение колебаний имеет вид:

х = Аsin 0t.

Исходя из этого уравнения определим момент времени t1, соответствующий смещению точки х = А/2. Имеем:

откуда t1 = T /12 .

Значение средней скорости точки при ее движении из положения равновесия определяется из формулы:

S A

cр1 t 2t1 ; ср1 = 100 см/с.

Время движения точки из крайнего положения до половины амплитуды будет равно:

27