Практикум по высшей математике. дифференциальное исчисление. Пантелеев И.Н

40. Областью определения функции является совокупность всех значений аргумента, при которых данное аналитическое выражение имеет смысл.

50. Преобразование графиков при некоторых простейших изменениях функции y = f(x):

а) график функции y = f (x - a) получается из исходного переносом всех точек на а единиц по оси абсцисс вправо, если а положительно, и влево, если а отрицательно;

б) график функции y = f(x)+b получается из исходного переносом всех точек на b единиц по оси ординат вверх, если b положительно, и вниз, если b отрицательно;

в) график функции y=Af(x) (А > 0) получается из исходного растяжением его вдоль оси ординат в А раз, если

исходного при k >1 уменьшением абсцисс в k раз, а при k < 1

увеличением абсцисс в 1k раз, если же k < 0, то абсциссы

меняют знак и график функции симметричен относительно оси Оy.

Последовательно выполняя рассмотренные сдвиги и деформации графика исходной функции, можно получить график и функции более сложного вида

f(x) = A f [ k(x - a)] + b.

3.1. Дана функция f(x) = 2х3- х2 + xx +−14 - 3. Найти частное

значение функции при х = 1.

Решение. Чтобы найти частное значение функции при х = 1, достаточно это значение аргумента подставить вместо х.

Получим f(1)= 2 13 – 12 + 11+−14 -3 = -2.

91

3.2. Дана функция f(x) = х2 + log a х + sin πax .

Найти значение функции при х = а.

Решение. Подставляем вместо х ее частное значение f(a) = а2 + log a а + sin πaa = а2 +1.

3.3. Функция задана параметрически

x = a cost,y = bsin t.

Требуется записать эту функцию в неявном виде.

Решение. Чтобы записать функцию в неявном виде, следует исключить параметр t. Возводя в квадрат

(x)2 = (a cos t)2

+

( y)2 = (b sin t)2

и преобразуя, получим

3.4. Построить графики функций:

− 2x + 4 при x ≥ 2.

92

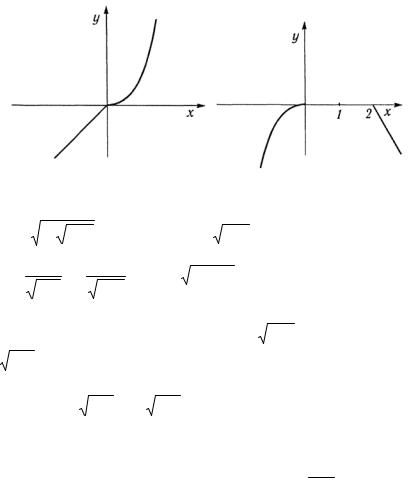
Решение.

а) Строим график функции для x ≤ 0 и для x > 0 (рис. 1.1).

б) Строим график функции последовательно для участков:

х < 0; 0 ≤ х < 2; х >2 (рис. 1.2).

и 1+x ≤ 1; 1+x ≤1; x ≤0 x [-1, 0].

б) Выражение под знаком логарифма должно быть больше

неравенства должны выполняться одновременно, то x (-3,1].

в) Выражение имеет смысл, когда -1 ≤ x1−3 ≤ 1 и x≠3.

Отсюда

93

г) Выражение имеет смысл при х - 1 > 0 и 5 - х > 0 . Решая эту систему неравенств, имеем х >1 и х < 5. Отсюда x (1,5).

д) В силу свойств логарифмической и степенной функции имеем следующую систему неравенств: sin x>0 и lg(sinx) ≥0.

Решение. а) За исходную функцию возьмем y=sin х, а

данную функцию представим в виде y=2sin3(x - 2 ). В данном

3

случае A=2; k =3; a = 2 .

3

1. Строим одну волну синусоиды (рис. 1.3).

Рис. 1.3

94

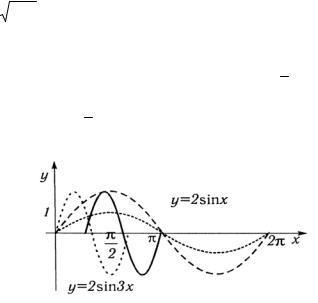
2. Увеличиваем ординаты всех точек в два раза y= 2 sin x.

3.Уменьшаем в три раза абсциссы точек графика и строим график функции y = 2 sin 3x.

4.Переносим точки графика функции y = 2sinЗх на 23

вправо по оси абсцисс, получаем график одной волны данной функции.

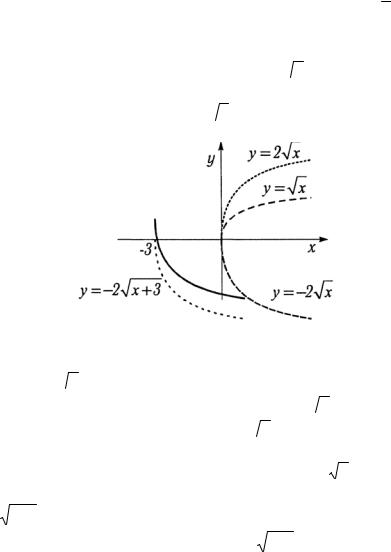
б) За исходную функцию возьмем у = у x . В данном случае A=-2; а = -3; b = 1.

1. Строим график функции у = у x (рис. 1.4).

Рис. 1.4

2.Увеличивая ординаты в два раза, строим график функции у =2 x .

3.Меняем знак на противоположный у = -2 x . График

этой функции симметричен графику у = 2 x относительно оси абсцисс.

строим график данной функции.

95

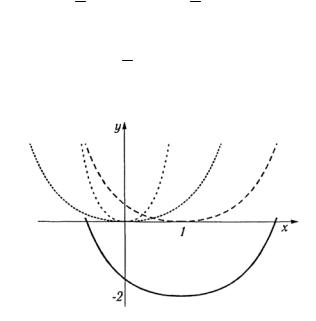
в) Преобразуем данную функцию к виду

y = 12 (x2-2x+1) - 2 = 12 (x-1)2 - 2.

За исходную функцию возьмем y = x2. В данном случае

A = 12 , a = 1, b= -2.

1. Строим график исходной функции y = x2 (рис. 1.5).

Рис. 1.5

2. Уменьшаем ординаты графика функции в два раза и

96

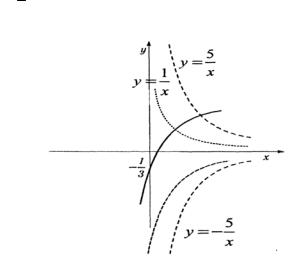
Выполняем следующие последовательные преобразования (рис. 1.6): строим пока только одну ветвь гиперболы; растягиваем по оси Оу в пять раз; заменяем графиком, симметричным относительно оси Ох; строим вторую ветвь гиперболы; делаем горизонтальный сдвиг координатной

системы на 3 единицы вправо и вертикальный сдвиг на 3

2

единицы вниз.

Рис. 1.6

97

1.4. Вычисление пределов. Раскрытие неопределенностей

10. Число b называется пределом функции f(x) при х → а, если для любого ε >0 найдется такое δ >0, что | f (х) - b|< ε как

только |х — а| < δ . Обозначают предел lim f (x) = b .

x→a

Предел функции f(х), если он существует, при стремлении

x к a справа обозначают lim f (x) .

x→a+0

Аналогично, предел функции при стремлении х к а слева

98

делением числителя и знаменателя на множитель, стремящийся к нулю, или с помощью первого замечательного предела.

60. Неопределенность вида ( ∞− ∞) раскрывается делением на х в старшей степени.

70. Неопределенность вида (0 ∞) и ( ∞− ∞) раскрывается

путем преобразования функции к неопределенностям 0 или

0

( ∞− ∞).

80. Неопределенность вида (1∞ ) раскрывается посредством преобразования предела ко второму замечательному пределу.

90. Бесконечно малые функции α(x) и β(x) называются

следующим правилом.

Предел отношения двух бесконечно малых не изменится, если их под знаком предела заменить на эквивалентные. Обозначая эквивалентность бесконечно малых следующим образом α(x) β(x) при x → 0, запишем наиболее известные

99

б) Разлагаем числитель и знаменатель на множители

в) Поскольку при x = 1 многочлены в числителе и знаменателе обращаются в ноль, то их можно разложить на множители, причем одним из сомножителей будет (х - 1). Тогда, деля многочлены на (х - 1) получим

100