
Учебное пособие 1740
.pdf
th x = |
sh x |
|
cth x = |
ch x |
|
2 |
2 |
|
, |
|
, |
ch |
x – sh x =1. |
||
ch x |
sh x |
Найдем производные для гиперболических функций, при этом напомним, что
(e–x)' = e–x (–1) = –e–x (как производная сложной функции):
|
|
|
x |
− e |
−x |
′ |
|
|
1 |
|
|
|
|
|
|
|
|
e |
x |
+ e |
−x |
|
|||||||||
(sh x) |
′ |
|
e |
|
|
|
|
|
= |
((e |
x |
) |
′ |
− (e |
−x |
′ |
|
|
|
|
= ch x. |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
= |
|
2 |
|
|
|
|
2 |
|
|
|
) ) = |
|
|
2 |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Итак, (shx)' = chx. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Аналогично доказывается, что (chx)' = shx. |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
(th x)′ = |
sh x ′ |
= |
|
ch x chx −shx shx |
= |
ch 2 x −sh 2 x |
. |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
ch 2 x |
|
|
|
|
ch 2 |
x |
|||||||||||||||||||
|
|
|
|
ch x |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
Так как ch2x – sh2x =1, то получаем: (th x)′ = |
|
|
|
1 |
|
. |
|
||||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ch 2 x |
|
|||||
Аналогично можно показать, что (cth x)′ = − |
|
|
|
1 |
. |
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sh 2 x |
|
||||||
2.5. Дифференцирование функций, заданных неявно. Логарифмическое дифференцирование
Пусть переменные x, y связаны между собой некоторым уравнением
F(x, y) = 0, |
(2.1) |
причем y является функцией от x, тогда говорят, что функция y задана неявно уравнением (2.1).
Например, уравнение y3 – 5x2 – 3x = 0 задает неявно функцию y, которую можно из этого уравнения выразить через x явно: y = 3 3x +5x 2 .
Уравнение x2 + y2 = a2 неявно задает две функции: y =  a 2 − x 2 и y = –
a 2 − x 2 и y = –  a 2 − x 2 .
a 2 − x 2 .
51
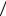
Однако не всегда, функции, заданные неявно могут быть выражены явно через элементарные функции. Так, из уравнения y + x = 2siny, которое неявно задает функцию y, нельзя выразить y явно через элементарные функции.
Как найти y' для функции, заданной неявно, уравнением (2.1)? Для этого надо найти производные по x от обеих частей этого уравнения, помня, что y – функция от x и приравнять эти производные. Из полученного уравнения найти y'.
Например, найдем y' для функции, заданной неявно уравнением x2 + y2 = a2:
(x2 + y2 )′ |
= (a2 )′ |
, 2x + 2y y' = 0, |
x |
x |
|
отсюда y' = – x y . |
|
|
Применим этот метод для нахождения производной для показательно-степенной функции y = u(x)v(x), где u(x) > 0, u(x), v(x) – дифференцируемые функции.
Прологарифмируем равенство y = uv, получим:
|
|
|
|
|
lny = v lnu. |
|
|
|
Дифференцируем полученное равенство: |
|
|
||||||
|
1 |
y' = v' lnu + v |
1 |
u', |
откуда y' = y(v' lnu + v |
1 |
u'), |
|
|
|
|
u |
|||||
|
y |
|
u |
|
|
|||
подставляя сюда |
y = uv, |
имеем: |
|
|
||||
|
|
|
y' = uv lnu v'+ v uv–1 u'. |
|
|
|||
Этот прием |
нахождения производной |
|
называется |
|||||
логарифмическим дифференцированием.
Пример. y = xsinx, (x > 0). Найти y'. Решение. lny = sinx lnx, (lny)' = (sinx lnx)',
52

1y y' = cosx lnx + sinx 1x , y' = xsinx(cosx lnx + sinx 1x )
или y' = xsinxcosx lnx + sinx xsinx – 1.
2.6. Функции, заданные параметрически, и их дифференцирование
Рассмотрим задание линии на плоскости, при котором переменные x, y являются функциями третьей переменной t (называемой параметром):
x =ϕ(t) |
. |
(2.2) |
|
||
y = g(t) |
|
|
Для каждого значения t из некоторого интервала соответствуют определенные значения x и y, а, следовательно, определенная точка M (x, y) плоскости. Когда t пробегает все значения из заданного интервала, то точка M (x, y) описывает некоторую линию L. Уравнения (2.2) называются параметрическими уравнениями линии L.
Если функция x = ϕ(t) имеет обратную t = Φ(x), то подставляя это выражение в уравнение y = g(t), получим y = g(Φ(x)), которое задает y как функцию от x. В этом случае говорят, чтоуравнения(2.2) задаютфункциюy параметрически.
Пример 1. Пусть M (x, y) – произвольная точка окружности радиуса R и с центром в начале координат. Пусть t – угол между осью Ox и радиусом OM (см. рис. 2.3). Тогда x, y выражаются через t:
x = R cos t |
, 0 ≤ t ≤ 2π, |
(2.3) |
|
||
y = R sin t |
|
|
Уравнения (2.3) являются параметрическими уравнениями окружности. Исключим из уравнений (2.3) параметр t. Для этого каждое из уравнений возведем в квадрат и сложим, получим:
53
x2 + y2 = R2(cos2t + sin2t) или x2 + y2 = R2 – уравнение окружности в декартовой системе координат. Оно определяет две
функции: y = R2 − x2 и y = – |
R2 − x2 . |
|
|
Каждая из этих функций задается параметрическими |
|||
уравнениями (2.3), но для первой функции t [0, π], |
а для |
||
второй t [π, 2π]. |
|
|
|
Пример 2. Параметрические уравнения |
|
||
x = a cost |
, 0 ≤ t ≤ 2π |
(2.4) |
|
|
|
||
y = bsin t |
|
|
|
задают эллипс с полуосями a, b (рис. 2.4). Исключая из уравнений параметр t, получим каноническое уравнение эллипса:
|
|
|
|
|
|
|
|
x2 |
|
y2 |
|
|
|||
|
|
|
|
|
|
|
|
|
+ |
|
= 1. |
|
|
|
|
|
y |
|
|
|
|
|
a2 |
b2 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
y |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
x |
|
|
|
|
|
x |
||
0 |
|
|
|
R |
|
|
|
|
|||||||
|
|
|
|
|
|
|
a |
||||||||
|
|
|
|
|
|
0 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
Рис. 2.4 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|||||
Рис. 2.3 |
|
|
|
|
|
|
|
|
|
|
|||||
Пример 3. Циклоидой называется линия, описанная точкой, лежащей на окружности, если эта окружность катится без скольжения по прямой (рис. 2.5). Введем параметрические уравнения циклоиды. Пусть радиус катящейся окружности равен a, точка M, описывающая циклоиду, в начале движения совпадала с началом координат. Определим координаты x, y точки M после того, как окружность повернулась на угол t (рис. 2.5), t = MCB. Длина дуги MB равна длине отрезка OB, так как окружность катится без скольжения, поэтому
OB = at, AB = MD = asint, CD = acost,
54
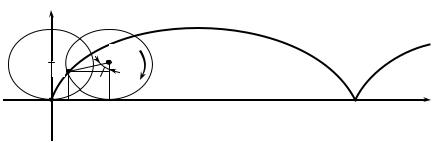
x = OB – AB = at – asint = a(t – sint),
y = AM = CB – CD = a – acost = a(1 – cost).
Итак, получены параметрические уравнения циклоиды:
x = a(t −sin t) |
(2.5) |
|
|
− cost) |
|
y = a(1 |
|
|
При изменении параметра t от 0 до 2π окружность поворачивается на один оборот, при этом точка M описывает одну арку циклоиды. Уравнения (2.5) задают y как функцию от x. Хотя функция x = a(t – sint) имеет обратную функцию, но она не выражается через элементарные функции, поэтому функция
y |
|
|
|
a M |
C |
|
|
D |
|
|
|
t |
|
|
|
0 A |
B |
2πa |
x |
|
|
Рис. 2.5 |
|
y = f (x) не выражается через элементарные функции. Рассмотрим дифференцирование функции, заданной па-
раметрически уравнениями (2.2). Функция x = ϕ (t) на некотором интервале изменения t имеет обратную функцию t = Φ (x), тогда y = g(Φ(x)). Пусть x = ϕ (t), y = g (t) имеют производные, причем xt′ ≠ 0. По правилу дифференцирования сложной
функции y′ |
= y′ t′ |
. На основании правила дифференцирова- |
||||||||
x |
t x |
|
|
1 |
|
|
|
|
|
|
ния обратной функции t′ |
= |
|
|
, |
поэтому: |
|||||
|
|
|
|
|||||||
|
|
x |
|
x′ |
|
|
|
|||
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
y |
′ |
|
|
|
|
|
|
y′ |
= |
|
|
t |
. |
(2.6) |
||
|
|
|
|
|
||||||
|
|
x |
|
|
x′ |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
t
55
Полученная формула (2.6) позволяет находить производную для функции, заданной параметрически.
Пример 4. |
Пусть функция y, зависящая от x, задана па- |
|||
x = a cos t, |
0 |
≤ t ≤ π. Найти |
y′x . |
|
раметрически: |
|
|||
y = bsin t, |
|
|
|
|
Решение. |
y′ |
= |
yt′ |
= |
b cos t |
= – |
b |
ctgt. |
|
x |
|
x′ |
|
− a sin t |
|
a |
|
|
|
|
t |
|
|
|
|
|
Пример 5. Найти угловой коэффициент k касательной к циклоиде в точке M0, соответствующей значению параметра
t0 = π .
4
Решение. Из уравнений циклоиды: |
|
|
|||||||
y′ |
= asint, |
x′ = a(1 – cost), поэтому |
|
|
|||||
t |
|
t |
|
|
|
|
|
|
|
|
|
|
y′ |
a sin t |
|
|
sin t |
|
|
|
|
y′ = |
t |
= |
|
= |
|
|
. |
|
|
x |
x′ |
a(1 − cos t) (1 |
−cos t) |
|
|||
|
|
|
t |
|
|
|
|
|
|
Угловой коэффициент касательной в точке M0 равен значению y′x при t0 = π 4 :
4 :
|
sin |
π |
|
|
|
|
|
2 |
|
|
2 |
|
2(2 + |
2) |
|
2 |
2 + 2 |
|
|
|
k = |
4 |
|
= |
|
|
|
2 |
|
= |
= |
= |
= |
2 +1, |
|||||||
|
|
π |
|
|
|
2 |
2 − 2 |
4 − 2 |
|
|
2 |
|||||||||
1 − cos |
4 |
|
1 − |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
k = |
2 +1. |
|
|
|
|
|
|
|
2.7. Дифференциал функции
Пусть функция в точке x0 имеет производную. По определению:
56
|
lim |
y |
= f ′(x0), поэтому по свойствам предела (разд. 1.8) |
|||||
|
x→0 |
x |
|
|
|
|
|
|
y = f (x0) + α, где α – бесконечно малая при |
x → 0. Отсюда |
|||||||
x |
|
|
|
|
|
|
|
|
|
|
|
y = |
f ′(x0) |
x + α x. |
|
(2.7) |
|
|
При x → 0 второе слагаемое в равенстве (2.7) является |
|||||||
бесконечно малой высшего порядка, по сравнению с |
x: |
|||||||
lim |
α |
x = |
lim α = 0, поэтому y и f ′(x0) |
x – эквивалент- |
||||
x→0 |
x |
|
x→0 |
|
|
f ′(x0) ≠ 0). |
|
|
ные, бесконечно малые (при |
|
|
||||||
|
Таким образом, приращение функции |
y состоит из двух |
||||||
слагаемых, |
из которых |
первое f ′(x0) x является главной |
||||||
частью |
приращения |
y, |
линейной относительно |
x (при |
||||
f ′(x0) ≠ 0).
Дифференциалом функции f (x) в точке x0 называется главная часть приращения функции и обозначается: dy или df (x0). Следовательно,
df (x0) = f ′(x0) x. |
(2.8) |
Пример 1. Найти дифференциал функции dy и приращение функции y для функции y = x2 при:
1) произвольных x и x; |
2) x0 = 20, x = 0,1. |
Решение
1) y = (x + x)2 – x2 = x2 + 2x x + ( x)2 – x2 = = 2x x + ( x)2, dy = 2x x.
2) Если x0 = 20, x = 0,1, то
y = 40 0,1 + (0,1)2 = 4,01; dy = 40 0,1= 4.
Запишем равенство (2.7) в виде: 57
y = dy + α x. |
(2.9) |
Приращение y отличается от дифференциала dy на бесконечно малую высшего порядка, по сравнению с x, поэтому в приближенных вычислениях пользуются приближенным ра-
венством y ≈ dy, если |
x достаточно мало. |
|
Учитывая, что |
y = f (x0 + x) – f (x0), |
получаем при- |
ближенную формулу: |
|
|
f(x0 + x) ≈ f(x0) + dy. |
(2.10) |
|
Пример 2. Вычислить приближенно |
4,1 . |
|
Решение. Рассмотрим: f(x) =  x ; x0 = 4, x = 0,1; тогда 4,1 = f(x0 + x). Используя формулу (2.10), получим:
x ; x0 = 4, x = 0,1; тогда 4,1 = f(x0 + x). Используя формулу (2.10), получим:
4,1 = f (x0 + |
x) ≈ f (x0) + dy, |
f (x0) = 4 =2, |
dy = f'(x0) x = |
||||
|
|
1 |
0,1 = |
0,1 |
= 0,025. |
|
|
|
|
2 |
4 |
|
|
||
|
|
4 |
|
|
|
||
Значит, |
4,1 |
≈ 2,025. |
|
|
|
|
|
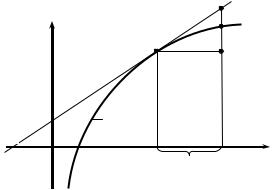
Рассмотрим |
геометрический |
смысл |
дифференциала |
||||
df(x0) (рис. 2.6). |
|
|
|
|
|
|
|
Проведем |
к графику функции y = f (x) |
касательную в |
|||||
точке M0(x0, f (x0)), пусть ϕ – угол между касательной KM0 и
осью Ox, тогда f '(x0) = tgϕ. Из M0NP:
PN = tgϕ x = f '(x0) x = df(x0).
Но PN является приращением ординаты касательной при изменении x от x0 до x0 + x. Следовательно, дифференциал функции f (x) в точке x0 равен приращению ординаты касательной.
Найдем дифференциал функции y = x. Так как (x)' = 1, то dx = 1 x = x. Будем считать, что дифференциал независимой переменной x равен ее приращению, т.е. dx = x.
58
Если x – произвольное число, то из равенства (2.8) полу-
чаем df(x) = |
f ′(x)dx, откуда f ′(x) = |
df (x) |
или |
f ′(x) = |
dy |
. |
dx |
|
|||||
|
|
|
|
dx |
||
Таким образом, производная для функции y = f (x) равна отношению ее дифференциала к дифференциалу аргумента.
P
y
M  ϕ M N
ϕ M N
y = f(x)
K  ϕ
ϕ
0 |
|
x0 |
|
|
x0 + x x |
|
|
x |
|||
|
Рис. 2.6 |
|
|
|
|
Рассмотрим свойства дифференциала функции.
Еслиu(x), v(x) – дифференцируемыефункции, тосправедливыследующиеформулы:
d(u + v) = du + dv; d(u v) = u dv + v du;
u |
= |
du v −u dv |
, (v ≠ 0). |
d |
v2 |
||
v |
|
|
(2.11)
(2.12)
(2.13)
Для доказательства этих формул используются формулы производных для суммы, произведения и частного функции. Докажем, например, формулу (2.12):
d(u v) = (u v)' x = (u v' + u' v) x = =u v' x + u' x v = u dv + v du.
Рассмотрим дифференциал сложной функции:
59
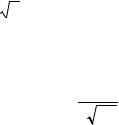
y = f (x), x = ϕ (t), т.е. y = f (ϕ (t)). |
|
|||
Тогда dy = |
yt′dt, но |
yt′ = y′x xt′ , |
поэтому dy = |
y′x xt′ dt. |
Учитывая, что |
x′dt = dx, |
получаем |
dy = y′ dx = f ′ |
(x)dx. |
|
t |
|
x |
|
Таким образом, дифференциал сложной функции y = f(x), где x = ϕ (t), имеет вид dy = f ′(x)dx, такой же, как в том слу-
чае, когда x является независимой переменной. Это свойство называется инвариантностью формы дифференциала.
2.8. Производные и дифференциалы высших порядков
Пусть функция f (x) определена и дифференцируема на некотором промежутке X, тогда ее производная f ′(x) также
является функцией от x на этом промежутке. Если f ′(x) имеет
производную на промежутке X, то эта производная называется
производной второго порядка функции y = f (x) и обозначает-
ся: y'' или f ′′(x).
Итак, f ′′(x) = ( f ′(x))'.
Производная от производной второго порядка называется
производной третьего порядка и обозначается: y''' или f ′′′(x).
Вообще, производной n-го порядка называется произ-
водная от производной (n – 1)-го порядка и обозначается: y(n)
или f (n)(x). Итак, f (n)(x) = (f (n-1)(x))'.
Производные y'', y''', ... называются производными высших порядков.
Пример 1. f (x) = |
|
x |
. Найти |
f ′′′(x) |
и f ′′′(4). |
|
|
|||
Решение. f ′(x) = |
(x1/ 2 )′ = |
1 |
|
x−1/ 2 , |
f ′′(x) = – |
1 |
x−3 / 2 , |
|||
|
4 |
|||||||||
|
|
|
2 |
|
|
|
|
|
||
f ′′′(x) = |
|
3 |
x−5 / 2 = |
3 |
, |
|
|
|
||
8 |
8 x5 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|||
60
