
Диагностика и испытание радиотехнических систем. Никитин Л.Н., Муратов А.В
.pdfМИНИСТЕРСТВО ОБЩЕГО И ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
Воронежский государственный технический университет
Л.Н.Никитин
ДИАГНОСТИКА И ИСПЫТАНИЕ РАДИОТЕХНИЧЕСКИХ СИСТЕМ
Учебное пособие
Воронеж 1999
УДК 621.396.664
Диагностика и испытание радиотехнических систем: Учеб. Пособие/ Л.Н.Никитин; Воронеж: Изд-во ВГТУ, 1999. 129 с.
Учебное пособие предназначено для студентов специальности 200800 “Проектирование и технология РЭС”, изучающих курс “Диагностика и испытание телевизионных систем” и может быть использовано студентами других специальностей радиотехнического профиля и аспирантами, занимающимися изучением и исследованием технологических процессов при проектировании и изготовлении радиотехнических устройств и радиосистем.
Тематика учебного пособия соответствует программе дисциплины, утвержденной методической комиссией радиотехнического факультета.
Ил. 54. Библиогр.: 6 назв.
Научный редактор д-р техн. наук, профессор А.В.Муратов.
рецензенты: кандидат физ. матем. наук, А.Н.Лукин; кафедра ФТТ ВГУ.
Рукопись набрана в текстовом редакторе WORD 8.0 и записана на магнитный диск в архиве файла RAR, включающего текст и внедренную графику.
Печатается по решению редакционно-издательского совета Воронежского государственного технического университета.
©Никитин Л.М., 1999.
©Оформление. Издательство
Воронежского государственного технического универси-
тета, 1999.
ВВЕДЕНИЕ
Широкое использование радиоэлектронных средств (РЭС) в различных областях науки и техники приводит к необходимости обеспечения высокой надежности ее работы при различных внешних воздействиях окружающей среды.
Об уровне надежности судят по способности РЭС безотказно работать в течение заданного времени в определенных условиях. Поэтому для оценки надежности и степени соответствия РЭС предъявляемым требованием осуществляют диагностику и испытания на всех этапах конструирования и производства. Полученная при этом информация о качестве работы РЭС и о причинах ее отказов совместно с данными реальной эксплуатации позволяет принять своевременные меры по совершенствованию схемы и конструкции, а также технологии производства.
Учебное пособие написано по программе курса “Диагностика и испытание видеотелевизионных систем”, читаемого в ВГТУ по специальности “Проектирование и технология РЭС“. В его основу положено комплексное изложение темы, в связи с чем информация о существующих видах диагностики и испытаний рассматривалась вцелом для обеспечения качества изделий.
Материал пособия излагается на основе действующих государственных и отраслевых стандартов.
1. Простые и сложные признаки
Пусть имеется система D, которая находится в одном из n возможных состояний. Эта система называется "система диагнозов", а каждое из состояний - диагнозом. В большинстве случаев непрерывные различные состояния системы представляются совокупностью эталонов (диагнозов), причем выбор числа диагнозов часто определяется задачами исследования. Распознавание состояний системы D осуществляется путем наблюдения за другой, связанной с ней системой, - системой признаков.
Простым признаком называется результат обследования, который может быть выражен одним из двух символов или двоичным числом (например, 1 и
0; + - и т.п.).
С точки зрения теории информации простой признак можно рассматривать как систему, имеющую одно из двух возможных состояний. Простой признак может означать наличие или отсутствие измеряемого параметра в определенном интервале; он может иметь и качественный характер./1/
Для целей диагностики область возможных значений измеряемого параметра часто разбивается на интервалы и характерным является наличие параметра в данном интервале. В связи с этим результат количественного обследования может рассматриваться как признак, принимающий несколько возможных состояний.
Условимся называть сложным признаком (разряда m) результат наблюдения (обследования), который может быть выражен одним из m символов. Если в качестве символов выбрать цифры, то сложный признак может быть выражен m-разрядным числом. Сложный признак может быть связан и с обследованием качественного характера, если оценка содержит несколько градаций (например, шум - увеличенный, нормальный, слабый - трехразрядный признак).
Разряды признака называются диагностическими интервалами. Разберем некоторые признаки.
Одноразрядный признак (m=1) имеет одно возможное состояние. Такой признак не несет какой-либо диагностической информации и его следует исключить из рассмотрения.
Двухразрядный признак (m=2) обладает двумя возможными состояниями.
Состояние двухразрядного признака Rj можно обозначить kj1 kj2. Трехразрядный признак имеет три возможные значения: kj1, kj2, kj3.

m - разрядный признак имеет m - возможных состояний kj1... kjm.
1.1. Диагностические веса признаков
Если в результате обследования выявлено, что признак kj имеет для данного объекта значение kjs, то это значение будем называть реализацией признака kj. Обозначая ее через kj* имеем kj* = kjs.
В качестве диагностического веса реализации признака kj для диагноза Di примем:
P(Di/kjs) |
|
|
ZDi = ZDi(kjs) = log2 |
, |
(1.1) |
P(Di) |
|
|
где P(Di/kjs) - вероятность диагноза Di при условии, что признак kj получил значение kjs; P(Di) - априорная вероятность диагноза.
С точки зрения теории информации величина ZDi(kjs) представляет собой информацию о состоянии Di, которой обладает состояние признака kjs.
Если вероятность состояния Di после того, как стало известно, что признак kj имеет реализацию в интервале s, увеличилась [P(Di/kjs/)> P(Di)], то ZDi(kjs)>0, т.е. диагностический вес данного интервала признака для данного диагноза положителен. Если наличие параметра в интервале s не изменяет вероятности диагноза, то ZDi(kjs) = 0, т.к. P(Di/kjs/) = P(Di). Наконец диагностический вес интервала s признака kj по отношению к диагнозу Di может быть отрицательным (отрицание диагноза). Диагностический вес наличия признака kj в интервале s можно записать в виде, более удобном для конкретных вычислений:
ZDi(kjs) = log2(P(kjs/Di)/P(kjs)), |
(1.2) |
где P(kjs/Di) - вероятность появления интервала s признака kj для объектов с диагнозом Di; P(kjs) - вероятность появления этого интервала у всех объектов с различными диагнозами.
Эквивалентность равенств (1) и (2) вытекает из тождеств:
P(kjs) P(Di/kjs) = P(Di) P(kjs/Di) = P(kjs Di). |
(1.3) |
1.2. Связь диагностических весов реализаций простого признака
Простой признак kj может иметь две реализации:
kj1 = kj; kj2 = k j (kj - наличие признака; k j - отсутствие признака).

В связи с этим можно говорить о наличии или отсутствии признака kj. Диагностический вес наличия признака kj для диагноза Di:
|
|
ZDi(kj) = log2[P(kj/Di)/P(kj)], |
(1.4) |
||||||||
Диагностический вес отсутствия признака: |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Z Di(kj) = log2[ P (kj/Di)/ P (kj)], |
(1.5) |
|||||||||
Т.к. существуют очевидные соотношения: |
|
||||||||||
|
|
|
|
|
|
||||||
|
|
|
|
P( |
k j |
) = 1 - P(kj) |
(1.6) |
||||
|
|
|
|
|
|
||||||
|
|
P (kj/Di) = 1 - P(kj/Di) |
(1.7) |
||||||||
то |
|
||||||||||
|
ZDi(kj) = log2([1 - P(kj/Di)]/[ 1 - P(kj) ]) |
|
|||||||||
|
|
= log2([1 - P(kj)2 ZDi(kj)]/[ 1 - P(kj) ]) |
(1.8) |
||||||||
Из формулы (1.8) вытекает, что ZDi(kj) и ZDi( k j ) всегда имеют равные знаки.
Если признак kj является случайным для данного диагноза [P(kj/Di) = P(kj)], то оба диагностических веса равны нулю.
1.3. Условный и независимый диагностические веса
Равенства (1.1) и (1.2) определяют независимый диагностический вес данной реализации признака для диагноза Di. Он характерен для ситуации, в которой обследование по признаку kj проводится первым или когда результаты обследования по другим признакам еще неизвестны (например, при одновременном обследовании по нескольким признакам).
Он также характерен для случая, когда вероятность появления данной реализации признака не зависит от результатов предыдущих обследований.
Однако известно, что диагностическое значение реализации признака во многих случаях зависит от того, какие реализации признаков получились в предыдущих обследованиях.
Бывает, что сам по себе признак не имеет особенного значения, но его появление после некоторого другого позволяет однозначно поставить диагноз (установить состояние системы).
1.4. Диагностический вес реализации комплекса признаков
Диагностический вес реализации комплекса признаков не зависит от порядка проведения обследования. Это справедливо и для двух (или

нескольких) комплексов признаков.
Отметим, что понятие диагностического веса реализации признака применимо только по отношению к данному диагнозу, как степень его подтверждения или отрицания. Усреднение диагностического веса по всем реализациям признака и по всем диагнозам приводит к понятию информативной или диагностической ценности обследования.
1.5. Диагностическая ценность обследования.
Частная диагностическая ценность обследования
Диагностический вес той или иной реализации признака еще не дает представления о диагностической ценности обследования по данному признаку. Например, при обследовании по простому признаку может оказаться, что его наличие не имеет диагностического веса, тогда как его отсутствие чрезвычайно важно для установления диагноза.
Условимся считать диагностической ценностью обследования по какому-либо признаку для конкретного диагноза величину информации, вносимую всеми реализациями признака в установлении этого диагноза.
Диагностическая ценность обследования учитывает все возможные реализации признака и представляет собой математическое ожидание величины информации, вносимой отдельными реализациями.
|
ZDi(kj) = m P(kjs/Di)ZDi(Rjs), |
(1.9) |
|
s 1 |
|
где Rjs - |
признак; Di - диагноз. |
|
Т.к. |
величина ZDi(Ri) относится только к одному диагнозу |
Di, то |
будем называть ее частной диагностической ценностью обследования по признаку kj.
Следует также отметить, что ZDi(kj) определяет независимую диагностическую ценность обследования. Она характерна для случая, когда обследование проводится первым, или когда результаты других обследований неизвестны. Величина ZDi(kj) может быть записана в трех эквивалентных формах:
m |
|
|
|
ZDi(kj) = |
P(kjs/Di)log2 |
[P(kjs/Di)/ P(kjs)]; |
(1.10) |
S 1 |
|
|
|
ZDi(kj) = m |
P(kjs/Di)log2 |
[P(Di/kjs)/ P(Di)]; |
(1.11) |
S 1 |
|
|
|
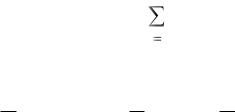
ZDi(kj) = m P(kjs/Di)log2 [P(Dikjs)/ P(Di) P(kjs)]. (1.12)
S1
1.6.Диагностическая ценность для простого признака
ZDi(kj) = P(kj/Di)log2 [P(kj/Di)/ P(kj)] +
+ P( k j /Di)log2 [P( k j /Di)/ P( k j )] = P(kj/Di)log2 [P(kj/Di)/ /P(kj)] +
+[1 - P(kj/Di)]log2([1 - P(kj/Di)] /[1- P(kj)]) |
(1.13) |
Если признак kj является случайным для диагноза Di , т.е. P(kj/Di)/ P(kj) = 1, то обследование по такому признаку не имеет диагностической ценности (ZDi(kj) = 0).
Наибольшую диагностическую ценность имеют обследования по признакам, которые часто встречаются при данном диагнозе, а вообще редко и, наоборот, по признакам, встречающимся при данном диагнозе редко, а вообще - часто. При совпадении P(kj/Di) и P(kj) обследование не имеет никакой диагностической ценности. Эти выводы совпадают с интуитивными правилами, используемые на практике, но теперь эти правила получают точную количественную оценку.
Диагностическая ценность обследования вычисляется в единицах информации (двоичных единицах или битах) и не может быть отрицательной величиной. Последнее понятно из логических соображений: информация при обследовании, не может "ухудшить" процесс распознавания действительного состояния.
1.7. Выбор величины диагностических интервалов
Величина ZDi(kj) может быть выбрана не только для оценки эффективности обследования, но и для целесообразного выбора величины диагностических интервалов (числа разрядов). Очевидно, что для упрощения анализа удобно уменьшить число диагностических интервалов, однако это может привести к уменьшению диагностической ценности обследования.
В примере, приведенном в [1, стр.147] видно, что диагностическая ценность обследования возросла вдвое при переходе от двух диагностических интервалов к четырем, а дальнейшее увеличение уже не привело к возрастанию ZDi(kj). Этот результат имеет общий характер. С увеличением числа диагностических интервалов диагностическая ценность признака возрастает или остается прежней, но анализ результатов становится более трудоемким. Следует иметь в виду, что увеличение числа
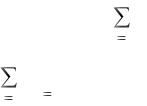
диагностических интервалов часто требует привлечения дополнительного статического материала для получения необходимой достоверности значения вероятностей интервалов.
1.8. Общая диагностическая ценность обследования
Известно, что обследование, обладающее небольшой диагностической ценностью для одного диагноза, может иметь значительную ценность для другого. Введем понятие общей диагностической ценности обследования по признаку kj для всей системы диагнозов D, определив ее как количество информации, вносимое обследованием в систему диагнозов:
|
ZD = n |
P(Di) ZDi(kj) = |
|
|
i 1 |
|
|
= n |
m |
|
|
P (Di)P(kjs/Di)log2 [P(kjs/Di)/ P(kjs)]. |
(1.14) |
||
i 1 |
s 1 |
|
|
Величина ZD(kj) представляет собой ожидаемое (среднее) значение информации, которое может быть внесено обследованием установление неизвестного заранее диагноза, принадлежащее рассматриваемой системе (совокупность) диагнозов.
1.9. Диагностическая ценность обследования по комплексу признаков
Общая диагностическая ценность
Рассмотрим сначала случай, когда комплекс признаков К состоит из двух признаков k1 и k2, имеющих m1 и m2 разрядов. Будем сначала считать, что результаты обследования по признаку k1 заранее неизвестны и требуется определить диагностическую ценность по одновременному обследованию k1
и k2.
Диагностическая ценность обследования по этому комплексу признаков для всей системы диагнозов измеряется количеством информации, вносимой системами k1 и k2 в систему D:
ZD(k1k2) = H(D) - H(D/k1k2), |
(1.15) |
где H(D) - априорная энтропия системы диагнозов; H(D/k1k2) - ожидаемая энтропия системы диагнозов после обследования по признакам k1 и k2.
Учитывая равенство:
H(Dk1k2) = H(k1) + H(k2 /k1) + H(D /k1k2), |
(1.16) |
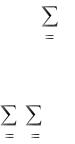
получим |
|
ZD(k1k2) = H(D) + H(k1) + H(k2 /k1) - H(Dk1k2). |
(1.17) |
Установим следующее важное равенство: |
|
ZD(k2 /k1) = H(D/k1) - H(D/k1k2). |
(1.18) |
Отметим, что H(D/k1) представляет собой ожидаемое значение энтропии системы диагнозов после проведения обследования по признаку k1, причем значения конкретной реализации признака k1 не требуется. Величина ZD(k2 /k1) выражает разность "средних" значений энтропии системы после обследования по признаку k1 и после обследования по комплексу признаков k1 и k2.
Частная диагностическая ценность
Определим частную диагностическую ценность для комплекса
признаков k1 и k2 для диагноза Di. |
|
|
ZD(k1 k2) = n |
P(Di) ZDi(k1 k2) |
(1.19) |
i1
Всоответствии с этим равенством частная диагностическая ценность:
ZDi(k1 k2) = m1 m 2 P(k1sk2p/Di)log2([P(k1sk2p/Pi)/
s 1p 1 |
|
/P(k1sk2p)]). |
(1.20) |
Будем считать признаки k1 и k2 независимыми при |
|
P(k2p/k1s) = P(k2p) |
(1.21) |
и условно независимыми для диагноза Di при |
|
P(k2p/Di k1s) = P(k2p /Di). |
(1.22) |
Если признаки k1 и k2 удовлетворяют условиям (1.21) и (1.22) |
|
одновременно (диагностически независимые признаки), то |
|
ZDi(k1 k2) = ZDi(k2) |
(1.23) |
и тогда |
|
ZDi(k1 k2) = ZDi(k1 ) + ZDi(k2) |
(1.24) |
Общий случай
Выше рассматривался комплекс двух признаков. Для комплекса Y
