Учебное пособие 1565

На практике получил большее распространение Графический метод приближённой оценки вещественных корней. Для этих целей строится гра-

фик функции по вычисленным её значениям.

Графически корни можно отделить 2-мя способами:

1. Построить график функции y = f(x) и определить координаты пересечений с осью абсцисс− это приближенные значения корней уравнения. На графике 3 корня.

Рис. 1. Отделение корней на графике f(x).

2. Преобразовать f(x)=0 к виду j(x) = y(x), где j(x) и y(x) – элементарные функции, и определить абсциссу пересечений графиков этих функций.

Рис. 2. Отделение корней по графикам функций j(x) и y(x).

Графический метод решения нелинейных уравнений широко применяется в технических расчётах, где не требуется высокая точность.

Для отделения вещественных корней можно использовать ЭВМ. Алгоритм отделения корней основан на факте Изменения знака функции в окрестности корня. Действительно, если корень вещественный, то график функции пересекает ось абсцисс, а знак функции изменяется на противоположный.

Рассмотрим схему алгоритма отделения корней нелинейного уравнения на заданном отрезке в области определения функции.

11

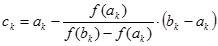
Алгоритм позволяет определить приближённые значения всех действительных корней на отрезке [a, b]. Введя незначительные изменения в алгоритм, его можно использовать для определения приближённого значения максимального или минимального корня.

Приращение неизвестного Δx не следует выбирать слишком большим, чтобы не «проскочить» два корня.

Недостаток метода – использование большого количества машинного времени.

Задания:

1)Исследовать уравнение f(x)=0 на отрезке [a;b] на существование и единственность корня, используя аналитический и графический методы.

2)Вычислить три приближения корня методом половинного деления и оценить погрешность последнего приближения.

Варианты заданий.

№1.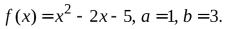

№2.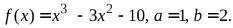

№3.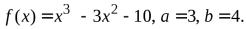

№4. .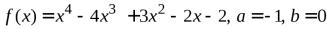

№5. .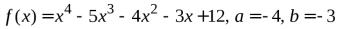

№6. .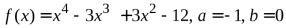

№7. .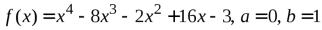

ЛАБОРАТОРНАЯ РАБОТА № 11 РЕШЕНИЕ НЕЛИНЕЙНЫХ УРАВНЕНИЙ МЕТОДАМИ ХОРД,

КАСАТЕЛЬНЫХ, КОМБИНИРОВАННЫМ МЕТОДОМ ХОРД И КАСАТЕЛЬНЫХ

Цель работы: получить навыки решения уравнений данными методами

Алгоритм нахождения корня нелинейного уравнения по методу хорд

1. Найти начальный интервал неопределенности 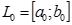одним из методов отделения корней. Задать погрешность расчета (малое положительное

число 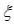) и начальный шаг итерации ().

2.Найти точку пересечения хорды с осью абсцисс:

3.Необходимо найти значение функции 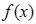в точках 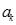, и 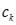. Далее необходимо проверить два условия:

12

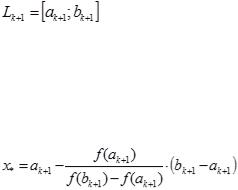
-если выполняется условие 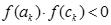, то искомый корень находится внутри левого отрезка положить, ;

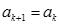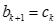-если выполняется условие 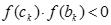, то искомый корень находится

внутри правого отрезка принять , .

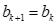В результате находится новый интервал неопределенности, на котором находится искомых корень уравнения:

4. Проверяем приближенное значение корня уравнения на предмет заданной точности, в случае:

- если разность двух последовательных приближений станет меньше за-

данной точности 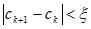, то итерационный процесс заканчивается. Приближенное значение корня определяется по формуле:

- если разность двух последовательных приближений не достигает необходимой точности 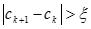, то необходимо продолжить итерационный процесс 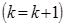и перейти к п.2 рассматриваемого алгоритма.

Задания:

1) Найти три приближения корня для уравнения f(x)=0 на отрезке [a; b] а) методом хорд; б) методом касательных. Вычислить погрешность третьего приближения для каждого метода.

2) Найти приближенный корень уравнения корень уравне-

ния на отрезке [a; b] с точностью до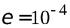комбинированным методом хорд и касательных.

Использовать варианты заданий для лабораторной работы № 10.

ЛАБОРАТОРНАЯ РАБОТА № 12

МЕТОД ПРОСТОЙ ИТЕРАЦИИ ДЛЯ НЕЛИНЕЙНЫХ УРАВНЕНИЙ

Цель работы: изучить метод простой итерации для нелинейных уравне-

ний

Чтобы применить метод простой итерации для решения нелинейного уравнения F(x)=0, необходимо преобразовать его к следующему виду:

13

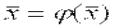
Это преобразование (приведение уравнения к виду, удобному для итерации) можно выполнить различными способами; некоторые из них будут рассмотрены ниже. Функция называется итерационной функцией.

Выберем каким-либо образом приближенное значение корня и под-

ставим его в правую часть уравнения (2). Получим значение .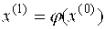

Подставим теперь 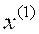в правую часть уравнения (2), имеем 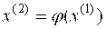. Продолжая этот процесс неограниченно, получим последовательность приближений к корню, вычисляемых по формуле

. (3)

Если существует предел построенной последовательности 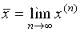, то,

переходя к пределу в равенстве (3) и предполагая функцию 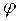непрерывной, получим равенство

(4)

Это значит, что – корень уравнения (2).

Ключевой момент в применении метода простой итерации – эквивалентное преобразование уравнения F(x)=0 к виду (2).

Способ 1. Если содержит в себе выражение некоторой обратимой

на [с; d] функции 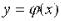, причем такой, что 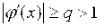на [c; d], то следует попытаться заменить уравнение на равносильное с использованием обратной

для функции 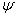: 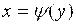. Этот способ основан на известном соотношении

между производными взаимообратных функций и следствии из него:

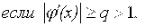То .

Прибавим к правой и левой частям х и получим: 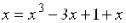. Проверим условие сходимости:

Пример. Привести уравнение к виду, пригодному для решения методом простой итерации на интервале [0,8; 2].

Прибавим к правой и левой частям х и получим: 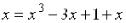. Проверим условие сходимости:

14

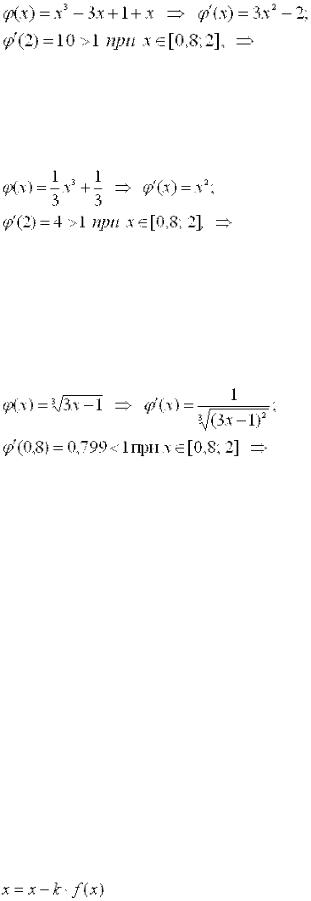
Условие сходимости не выполняется.

Другой вариант уравнения: 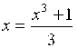. Проверим условие сходимости:

Условие сходимости не выполняется.

Так как ни одно из приведенных нами уравнений не удовлетворяет условию сходимости, то применим описанный способ:

;

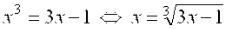Условие сходимости выполняется. Таким образом, для уточнения нужного нам корня методом простой итерации можно использовать уравнение

.

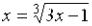Способ 2. В случае, когда способ 1 применить трудно или он не даст нужного результата, можно использовать следующий прием.

Пусть дано уравнение с единственным корнем в [a; b]. Предположим, что на отрезке [с; d] производная 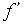функции F непрерывна, не равна констан-

те и принимает значения одного и того же знака. Будем считать, что 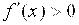, т. к. в противном случае можно рассматривать равносильное уравнение:

.

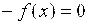Введем обозначения: .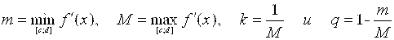

Ясно, что 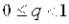. Заменим равносильное уравнение уравнением эквивалентным ему

15

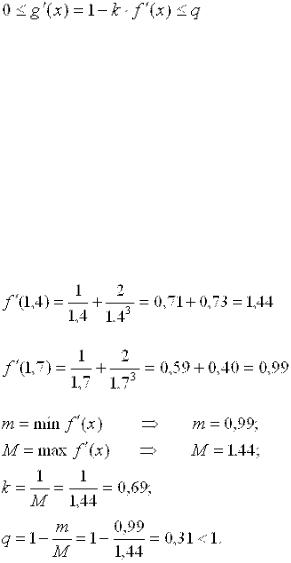
И покажем, что для функции 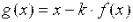на [c; d] имеет место условие сходимости.

Для 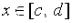справедливы неравенства: . Разделим их почленно на число М и для разностей между единицей и полученными дробями получим неравенство:

,

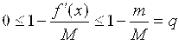Откуда и вытекает, что

При всех .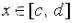

Пример. Привести уравнение 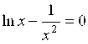к виду, пригодному для решения методом простой итерации на интервале [1,4; 1,7].

Так как условие сходимости не выполняется, то применим второй способ приведения уравнения:

;

;

;

Задания:

Методом простой итерации вычислить корень уравнения с точностью

до 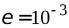. Отрезок, на котором корень существует и единственный, выделить самостоятельно.

16

Варианты заданий

№1. 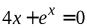. № 2. .

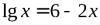№3. . № 4. .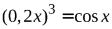

№5.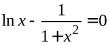. № 6. .

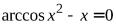№7. 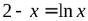. № 8. .

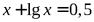ЛАБОРАТОРНАЯ РАБОТА№ 13 РЕШЕНИЕ СИСТЕМ НЕЛИНЕЙНЫХ УРАВНЕНИЙ

МЕТОДОМ НЬЮТОНА

Цель работы: получить навыки решения систем нелинейных уравнений методом Ньютона

Задания:

Решить систему уравнений с помощью метода Ньютона. Результаты получить с пятью верными знаками. Начальные приближения найти графически.

Варианты заданий.

№1. .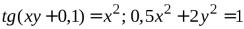

№2. .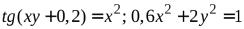

№3. .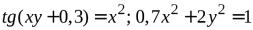

№4. .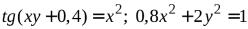

№5. .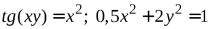

ЛАБОРАТОРНАЯ РАБОТА № 14 РЕШЕНИЕ ЗАДАЧ

ЗАДАНИЕ 1. ЦЕЛОЧИСЛЕННЫЕ ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ

Цель работы: получить навыки решения задач Задача 1. В текущем году заводу необходимо:

1)закупить два универсальных станка с ЧПУ общей стоимостью 200 тыс. руб. Для этого требуются трудовые ресурсы в объеме 250 человекодней и производственные площади 100 м2;

2)смонтировать транспортный конвейер стоимостью 100 тыс. руб. Необходимы трудовые ресурсы 190 человекодней и производственные площади 200 м2.

17

Для проведения этих мероприятий завод располагает финансовыми ресурсами 250 тыс. руб., трудовыми — 200 человекодней и производственными площадями 200 м2.

Недостаток средств и ресурсов можно компенсировать, проведя некоторые из следующих мероприятии:

1)внедрить новые резцы для обработки металла. Экономия трудозатрат

—130 человекодней, финансовые затраты — 50 тыс. руб.;

2)провести профилактический ремонт станочного парка. Трудозатраты

—10 человекодней, прибыль — 20 тыс. руб.;

3)внедрить систему контроля качества продукции. Экономия трудозатрат — 190 человекодней, затраты производственных площадей — 50 м2, прибыль — 5 тыс. руб.;

4)реализовать устаревшее оборудование. Трудозатраты — 60 человекодней, высвобождение производственных площадей — 200 м2, прибыль — 300 тыс. руб.;

5)провести инвентаризацию запасов материальных ресурсов. Трудозатраты — 20 человекодней, высвобождение производственных площадей —

150 м2.

Вопрос: Какое минимальное количество мероприятий следует провести, чтобы закупить станки с ЧПУ и смонтировать транспортный конвейер?

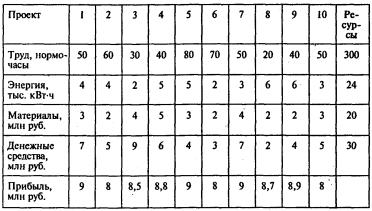
Задача 2. Для реконструкции машиностроительного предприятия было представлено 10 проектов, каждый из которых характеризуется четырьмя агрегированными показателями: затратами труда, энергии, материалов, денежных средств, а также ежегодной прибылью в случае реализации проекта. Соответствующие данные и объем имеющихся ресурсов приведены в таблице:

При выборе проектов необходимо учесть ряд ограничений технологического характера:

1)одновременно может быть реализовано не более семи проектов;

2)проекты 5 и 8 исключают друг друга;

3)проект 1 может быть реализован лишь при условии реализации проек-

та 2;

18

4) проект 4 может быть реализован лишь при условии реализации хотя бы одного из двух проектов: либо проекта 3, либо проекта 10.

Вопросы:

1.Какова максимальная прибыль?

2.Следует ли реализовывать проект 3?

ЗАДАНИЕ 2. ТРАНСПОРТНАЯ ЗАДАЧА

Задача 1. Фирма по прокату автомобилей «Золотое кольцо России» собирает заявки на аренду во всех городах центра России. Клиент имеет возможность получить автомобиль в любом удобном для него населенном пункте и оставить его в любом месте, где он заканчивает путешествие, в том числе и в своем родном городе. Работники фирмы забирают оставленные автомобили и перегоняют их для передачи новым клиентам.

Сейчас 4 автомобиля компании оставлены в Клину, 3 — в Ростове Великом, 6—в Ярославле и 1 — в Серпухове.

Имеются заказы на 5 автомобилей во Владимире, на 3 автомобиля в Санкт-Петербурге и на 6 автомобилей в Москве.

Расстояния между городами (в км) приведены в следующей таблице:

Составьте план, по которому следует перегонять автомобили новым клиентам. Ориентируйтесь на минимизацию расстояния, которое пройдут все перегоняемые автомобили.

Вопросы:

1.Чему равно минимальное расстояние, которое должны пройти все автомобили?

2.Сколько автомобилей следует перегнать в Москву из Ярославля?

3.На сколько увеличится минимальное расстояние, которое должны пройти все автомобили, если дополнительно стало известно, что еще один автомобиль оставлен в Серпухове и еще один клиент появился в Москве?

Задача 2. Фирма «Время — вперед» хочет разработать план сборки компьютеров. Прогноз спроса на компьютеры для каждого квартала следующего года показан в таблице:

19

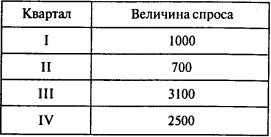
При работе в одну смену фирма может каждый квартал собирать 1200 компьютеров. Издержки по сборке одного компьютера составляют 10 тыс. руб. Если ввести вторую смену, то ежеквартально можно собирать еще 800 компьютеров. Однако сборка каждого компьютера во вторую смену обходится дороже — 11 тыс. руб. Компьютер может быть произведен в одном квартале, а сбыт

— в любом из последующих кварталов. В этом случае хранение каждого компьютера обходится в 500 руб. за квартал.

Составьте план производства, используя модель транспортной задачи. Вопросы:

1.Сколько компьютеров следует собрать в первом квартале, чтобы удовлетворить спрос с минимальными совокупными затратами?

2.На сколько процентов следует использовать мощности второй смены в первом квартале?

3.Сколько компьютеров следует собрать во втором квартале?

4.Сколько компьютеров следует собрать во втором квартале во вторую смену для сбыта в третьем квартале?

5.Каковы минимальные издержки?

ЗАДАНИЕ 3. ОСНОВЫ ТЕОРИИ ПРИНЯТИЯ РЕШЕНИЙ

Вопросы Вопрос 1. В теории принятия решении ситуация, которую не может кон-

тролировать лицо, принимающее решение, называется:

1)деревом решений;

2)состоянием среды;

3)решением в условиях неопределенности;

4)альтернативой;

5)таблицей решений.

Вопрос 2. Укажите правильное соответствие названий критериев принятия решений в условиях неопределенности:

1)minmax «критерий оптимизма»;

2)maxmin «критерий пессимизма»;

3)minmin «критерий пессимизма»;

4)maxmin «критерий безразличия»;

5)maxmax «критерий безразличия».

20