
Высшая математика. Контрольно-измерительные материалы для аттестации обучающихся в технических вузах. Алейников С.М., Горяйнов В.В
.pdf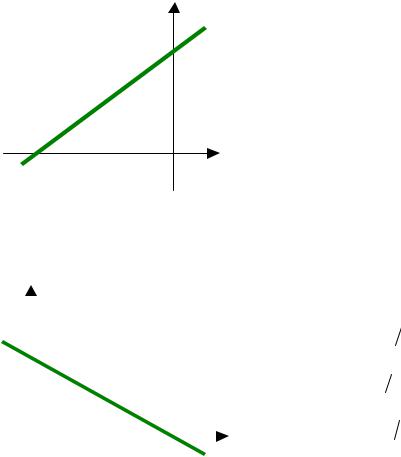
13. |
Прямые 3x − 2 y −7 = 0 и 3x + 2 y + 6 = 0 … |
|
а) пересекаются, |
б) параллельны, |
|
в) перпендикулярны, |
г) совпадают. |
|
14. |
Прямые 3x −5y −7 = 0 и 3x −5y + 6 = 0 … |
|
а) пересекаются, |
б) параллельны, |
|
в) перпендикулярны, |
г) совпадают. |
|
15. |
Прямые x − 2 y + 4 = 0 и 2x − 4 y +8 = 0 … |
|
а) пересекаются, |
б) параллельны, |
|
в) перпендикулярны, |
г) совпадают. |
|
16. |
Прямые x − 2 y + 4 = 0 и 2x + y +8 = 0 … |
|
а) пересекаются, |
б) параллельны, |
|
в) перпендикулярны, |
г) совпадают. |
|
17. Угловой коэффициент k прямой равен …
|
у |
а) –3, |
|
3 |
б) 1, |
|
|
в) –1, |
|
х |
г) 0, |
–3 |
0 |
д) 3. |
|
|
18. Угловой коэффициент k прямой равен …
у |
|
|
а) 2, |
|
|
|
|||
|
|
|
|
б) −3 2 , |
2 |
|
|
в) 2 3, |
|
|
|
|
|
|
|
|
|
|
г) −2 3 , |
0 |
3 |
|
|
|
|
|
х |
д) 3. |
|
|
|
|
|
|
|
|
|
|
31 |

19.Угловой коэффициент k прямой
у
0 |
5 |
х |
–1
20.Угловой коэффициент k прямой
у
х
–3 0
–2
равен … а) –1,
б) –5,
в) 1 5 ,
5 ,
г) −1 5 ,
5 ,
д) 5.
равен … а) 2,
б) −2 3 ,
3 ,
в) 2 3,
3,
г) −3 2,
2,
д) 3.
21. Уравнение прямой, перпендикулярной данной и проходящей через точку (2;−1),…
|
|
|
а) 3x + y −5 = 0 , |
|
у |
|
б) x +3y −5 = 0 , |
|
|
||
|
|
|
|
|
2 |
|
в) 3x − y −5 = 0 , |
|
|
х |
г) 3x + y +5 = 0 , |
|
|
|
|
–6 |
0 |
|
|
|
|
||
|
|
|
д) x +3y +5 = 0 . |
|
|
|
|
|
|
|
32 |

22. Уравнение прямой, перпендикулярной данной и проходящей через точку (−2;1),…
а) 4x +5y −3 = 0 ,
у
5б) 4x −5y +3 = 0 ,
в) 4x −5y −3 = 0 ,
|
|
|
|
г) 5x + 4 y +3 = 0, |
–4 |
0 |
х |
||
д) 4x +5y +3 = 0.
23. Уравнение прямой, перпендикулярной данной и проходящей через точку (−3;0),…
у |
|
а) 3x + 2 y −9 = 0, |
|
6 |
б) −3x + 2 y +9 = 0 , |
|
|
в) −3x + 2 y −9 = 0 ,
0 |
9 |
х |
г) |
− |
− |
2 y |
− |
9 |
= |
0 , |
|
|
|
3x |
|
|
|
д) 3x + 2 y +9 = 0 .
24. Уравнение прямой, перпендикулярной данной и проходящей через точку (−3;1),…
у |
|
|
7 |
|
|
0 |
7 |
х |
а) −x + y −4 = 0,
б) x + y − 4 = 0 ,
в) −x + y −7 = 0,
г) x + y −7 = 0 ,
д) −x − y − 4 = 0 .
33
25. Уравнение прямой, перпендикулярной данной и проходящей через точку (0;1),…
у |
|
|
7 |
|
|
0 |
7 |
х |
а) y − x −1 = 0,
б) x + y − 4 = 0 ,
в) −x + 2 y −7 = 0 ,
г) x + y +1 = 0 ,
д) −x − y − 4 = 0 .
3.1.2.Кривые второго порядка
26.Координаты вершины параболы y2 −6y −6x −9 = 0 имеют вид …
а) C (3;−3), |
б) C (−3;−3), |
в) C (3;3), |
г) C (−3;0), |
д) C (−3;3). |
|
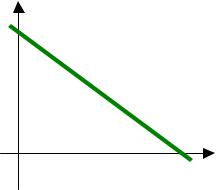
27. Уравнение 4x2 −3y2 + 20x +30 y +1 = 0 определяет … |
||
а) гиперболу, |
б) параболу, |
в) окружность, |
г) эллипс, |
д) прямую. |
|
28. Кривая 2x2 + 2 y2 − 4x + 6 y =9 имеет центр в точке с координатами …
а) |
|
|
3 |
|
, |
|
б) |
|
−1; |
− |
3 |
|
, |
в) |
|
− |
3 |
|
, |
1; |
2 |
|
|
|
2 |
|
1; |
2 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
г) |
|
−1; |
3 |
|
, |
д) |
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1;− |
4 |
. |
|
|
|
|
|
|
|
|||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
29. Кривая x2 + y2 − 4x + 6 y −10 = 0 имеет центр в точке с координата-
ми… |
|
|
а) (−2;−3), |
б) (2;−3), |
в) (2;3), |
г) (−2;3), |
д) (4;−6). |
|
30. Координаты вершины параболы x2 −6x −6 y −9 = 0 |
имеют вид … |
|
а) C (−3;−3), |
б) C (3;−3), |
в) C (3;3), |
|
34 |
|
г) C (−3;0), |
д) C (−3;3). |
|
31. Уравнение 2x2 +3y2 + 2x +3y +15 = 0 определяет … |
||
а) гиперболу, |
б) параболу, |
в) окружность, |
г) эллипс, |
д) прямую. |
|
32. Ветви параболы y2 + 4 y + 2x +8 = 0 направлены … |
||
а) влево, |
б) вправо, |
|
в) вниз, |
г) вверх. |
|
33. Радиус окружности x2 + y2 − 2x + 2 y −14 = 0 равен … |
||
а) 2, |
б) 3, |
в) 4, |
г) 5, |
д) 6. |
|
34. Координаты вершины параболы y2 − 4y −4x − 4 = 0 имеют вид …
а) C (−2;−2), |
б) C (−2;2), |
в) C (2;2), |
г) C (2;−2), |
д) C (−4;2). |
|
35. Уравнение 9x2 +9 y2 + 20x +30 y +19 = 0 определяет … |
||
а) гиперболу, |
б) параболу, |
в) окружность, |
г) эллипс, |
д) прямую. |
|
36. Кривая 2x2 + y2 − 4x + 4 y =9 имеет центр в точке с координатами …
а) (1;−2), |
б) (−1;−2), |
в) (1;2), |
г) (−1;2), |
д) (2;−1). |
|
37. Координаты вершины параболы x2 −4y − 4x − 4 = 0 имеют вид …
а) C (−2;−2), |
б) C (−2;2), |
в) C (2;−2), |
г) C (0;4), |
д) C (2;2). |
|
38. Кривая 2x2 +5y2 − 2x +5y =10 имеет центр в точке с координатами…
а) |
|
5 |
;− |
5 |
, |
|
б) |
|
− |
1 |
; |
1 |
|
, |
в) |
1 |
; |
1 |
|
, |
||
|
2 |
|
|
|
|
2 |
2 |
|
|
2 |
|
|||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|||||
г) |
|
− |
1 |
; |
− |
1 |
|
, |
д) |
|
1 |
;− |
1 |
|
|
|
|
|
|
|
|
|
|
2 |
2 |
|
|
|
2 |
. |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
||||
35
39. Уравнение 3y2 + 2x +3y +15 = 0 определяет … |
|
|
а) гиперболу, |
б) параболу, |
в) окружность, |
г) эллипс, |
д) прямую. |
|
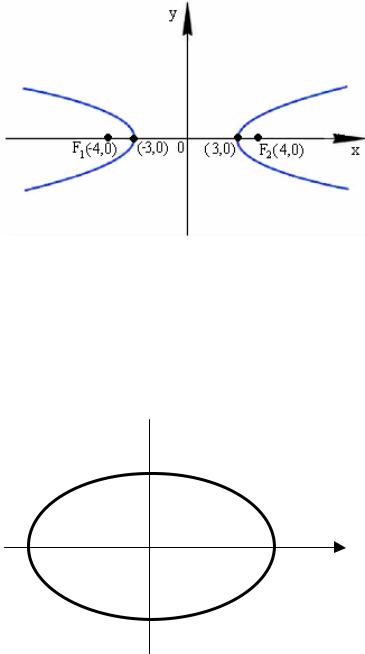
40. Каноническое уравнение гиперболы …
а) |
x2 |
− |
y2 |
=1, |
б) |
x2 |
+ |
y2 |
=1, |
в) |
x2 |
− |
y2 |
= 0 , |
|||
9 |
7 |
9 |
7 |
9 |
7 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
г) |
|
x2 |
− |
|
y2 |
=1, |
д) |
x2 |
− |
y2 |
=1. |
|
|
|
|
|
|
|
7 |
|
9 |
9 |
16 |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
41. Каноническое уравнение эллипса …
у
5
0 |
7 |
х |
а) |
x2 |
− |
y2 |
=1, |
б) |
x2 |
+ |
y2 |
=1, |
в) |
x2 |
+ |
y2 |
= 0 , |
|||
49 |
25 |
49 |
25 |
49 |
25 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
г) |
|
x2 |
− |
|
y2 |
= 0 , |
д) |
y2 |
+ |
x2 |
=1. |
|
|
|
|
|
|
|
49 |
|
25 |
49 |
25 |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
36 |
|
|
|
|
|
|
||

42. Ветви параболы y + 4x + 2x2 +8 = 0 направлены …
а) влево, |
б) вправо, |
|
|
||||||
в) вниз, |
г) вверх. |
|
|
||||||
43. Уравнение окружности… |
|
|
|
|
|
||||
|
|
|
|
|
у |
|
1 |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-1 |
|
|
0 |
х |
|||||
|
|
|
|
|
|
|
|
|
|
а) x2 −2x − y2 − 2 = 0 , |
б) x2 + 2x − 2 y + y2 − 4 = 0 , |
в) x2 − 2 y + y2 + 4 = 0 , |
г) x2 + 2x + y2 = 0, |
д) x2 + 2x + 2 y + 2 = 0 . |
|
44. Эксцентриситет эллипса равен… |
|
у |
|
5
0 |
7 |
х |
а) ε = |
12 , |
|
б) ε = |
49 6 |
, |
в) ε = |
25 6 |
, |
|||
|
25 |
|
49 |
||||||||
|
7 |
|
|
|
|
|
|
|
|||
г) ε = |
|
2 6 |
, |
д) ε = |
|
2 6 |
. |
|
|
|
|
5 |
|
7 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
37 |
|
|
|
|
|
|
|

45. Радиус окружности 2x2 + 2 y2 − 4x − 4 y − 28 = 0 равен… |
|
|
а) 2, |
б) 3, |
в) 4, |
г) 5, |
д) 6. |
|
46. Каноническое уравнение эллипса…
у
4
0 |
6 |
х |
а) |
x2 |
+ |
|
y2 |
=1, |
б) |
x2 |
|
− |
y2 |
=1, |
в) |
x2 |
+ |
y2 |
= 0 , |
||
36 |
16 |
36 |
|
16 |
36 |
16 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
г) |
|
y2 |
− |
|
x2 |
|
=1, |
д) |
y2 |
|
+ |
x2 |
=1. |
|
|
|
|
|
|
36 |
16 |
|
36 |
|
16 |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
47. Уравнение окружности…
у





 3
3
-3 |
0 |
х |
а) x2 + 6x + 6 y + y2 +9 = 0 , |
б) x2 + 6x −6 y − y2 +9 = 0 , |
|
в) x2 −6x −6 y − y2 +9 = 0, |
г) x2 +6x −6 y + y2 +3 = 0, |
|
д) x2 + 6x −6 y + y2 +9 = 0 . |
|
|
|
38 |
|
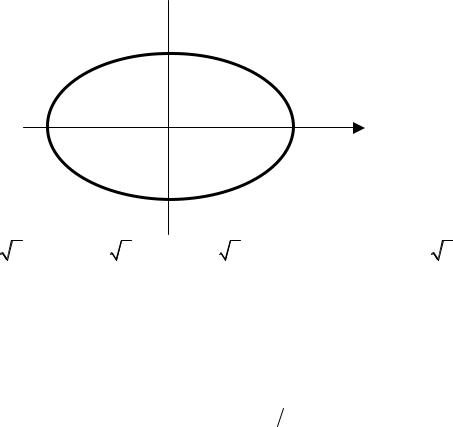
48. Эксцентриситет эллипса равен…
у
4
0 |
6 |
х |
а) ε = |
5 |
, б) ε = |
5 |
, в) ε = |
|
5 |
, г) ε = |
5 , д) ε = |
2 5 |
. |
|
3 |
|
6 |
|
|
2 |
|
3 |
3 |
|
49. Ветви параболы 4x + x2 +8 −3y = 0 направлены … |
|
|
||||||||
а) влево, |
|
|
б) вправо, |
|
|
|
||||
в) вниз, |
|
|
г) вверх. |
|
|
|
||||
50. Радиус окружности x2 + y2 −3x −3y −18 4 = 0 равен… |
|
|
||||||||
а) 2, |
|
|
|
б) 3, |
|
|
в) 4, |
|||
г) 5, |
|
|
|
д) 6. |
|
|
|
|
|
|
3.2.Аналитическая геометрия в пространстве
3.2.1.Плоскость в пространстве
51.Уравнение плоскости, проходящей через точку А(10,20,30) и параллельно плоскости yOz ,…
а) 10x + 20 y +30z = 0 , |
б) x =10 , |
в) 10x + 20 y =30 , |
г) y = 20 , |
д) x = −10 . |
|
52. Уравнение плоскости, проходящей через точку |
А(−2,−5,7) и парал- |
|
лельно плоскости xOz ,… |
|
|
а) −2x −5y + 7z = 0 , |
б) x = −2 , |
в) y +5 = 0 , |
г) −2x + 7z = −5 , |
д) −2x −5y + 7z + 2 = 0 . |
|
|
39 |
|

53. |
Уравнение плоскости, |
проходящей через точку А(8,−6,1) и парал- |
|
лельно плоскости xOy ,… |
|
|
|
а) 8x −6 y + z = 0, |
б) x =8 , |
в) y = 6 , |
|
г) z −1 = 0 , |
д) 8x −6 y = 0 . |
|
|
54. |
Параллельно оси OX проходит плоскость… |
|
|
а) 8y − 2z +1 = 0 , |
б) y + x =5 , |
в) y + x − z = 6 , |
|
г) 2x +3y − z −1 = 0 , |
д) 8x − y + z = 0. |
||
55. |
Параллельно оси OY проходит плоскость… |
|
|
а) x +3y +8z −4 = 0 , |
б) y + 4 = 0 , |
в) y − z = 6 , |
|
г) x + z −1 = 0, |
д) x −5y = 7 . |
|
|
56. |
Параллельно оси OZ проходит плоскость… |
|
|
а) −x + y +8z −3 = 0 , |
б) x + z = 0 , |
в) x + y −5z = 0 , |
|
г) z + 7 = 0 , |
д) 4x + y − 2 = 0 . |
||
57. |
Через ось OZ проходит плоскость… |
|
|
а) x − y + z −3 = 0 , |
б) 2x −3y = 0 , |
в) x + 2 y =5z , |
|
г) z −1 = 0 , |
д) y = 6z . |
|
|
58. |
Через ось OY проходит плоскость… |
|
|
а) 6z −5x = 0, |
б) y = 6 , |
в) 9 y =3z , |
|
г) 4x + y − z + 2 = 0, |
д) y − z +5 = 0 . |
|
|
59. |
Через ось OX проходит плоскость… |
|
|
а) 3x + z = 0, |
б) x = 2, |
в) 2 y = 3z , |
|
г) 8x +3y − 4z +1 = 0, |
д) y − z =8x . |
|
|
60. Уравнение плоскости, проходящей через точку А(0,1,2) и перпендекулярно вектору N {1;−1;0},…
а) x − y −1 = 0, |
б) x + y +1 = 0 , |
в) y + 2z −1 = 0, |
г) x − y +1 = 0 , |
д) y − 2z −1 = 0 . |
|
|
40 |
|
