Учебное пособие 1385

1. Основные понятия Марковских процессов

Внастоящее время теория Марковских процессов и

ееприложения широко применяются в самых различных областях науки и техники.

Благодаря сравнительной простоте и наглядности математического аппарата, высокой достоверности и точности получаемых решений, особое внимание Марковские процессы приобрели у специалистов, занимающихся исследованием операций и теорией принятия оптимальных решений.

Марковский источник полностью считается заданным (или определенным) следующими условиями:

1. Задано начальное распределение вероятностей цепи. Начальным распределением вероятностей

Марковской цепи называется распределение вероятностей состояний в начале процесса:

В частном случае, если начальное состояние системы S в точности известно S(0) = Si, то начальная вероятность Pi (0) = 1, а все остальные равны нулю.

2. Задан вектор переходных вероятностей цепи. Вероятностью перехода (переходной вероятностью)

на k-м шаге из состояния Si в состояние Sj называется условная вероятность того, что система S после k-го шага окажется в состоянии Sj при условии, что непосредственно перед этим (после k — 1 шага) она находилась в состоянии

Si.

Поскольку система может пребывать в одном из п состояний, то для каждого момента времени t необходимо

3

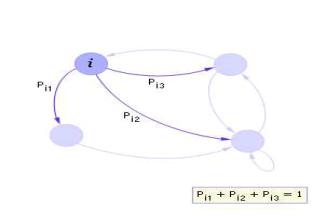
Рис. 1. Фрагмент графа переходов (переходы из i-го состояния являются полной группой случайных событий)

Каждый переход характеризуется вероятностью перехода Pij. Вероятность Pij показывает, как часто после попадания в i-е состояние осуществляется затем переход в j-е состояние. Конечно, такие переходы происходят случайно, но если измерить частоту переходов за достаточно большое время, то окажется, что эта частота будет совпадать с заданной вероятностью перехода.

Ясно, что у каждого состояния сумма вероятностей всех переходов (исходящих стрелок) из него в другие состояния должна быть всегда равна 1.

На основе матрицы перехода системы можно построить так называемый граф состояний системы, его еще называют размеченный граф состояний. Это удобно для наглядного представления цепи.

При рассмотрении конкретных систем удобно сначала построить граф состояний, затем определить вероятность переходов системы из одного состояния в то же самое (исходя из требования равенства единице суммы

5

элементов строк матрицы), а потом составить матрицу переходов системы.

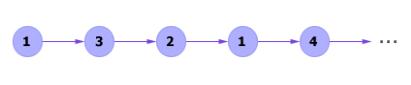
Реализация Марковского процесса (процесс его моделирования) представляет собой вычисление последовательности (цепи) переходов из состояния в состояние, как показано на рисунке 2. Цепь является случайной последовательностью и может иметь также и другие варианты реализации.

Рис. 2. Пример Марковской цепи, смоделированной по Марковскому графу, изображенному на рис. 1

При определении энтропии и количества информации в сообщениях, элементы которых охвачены корреляционными связями (т.е. коррелированы), что характерно для Марковской цепи, необходимо учитывать как безусловные, так и условные вероятности появления элементов.

Пусть сообщения составляют простую, т.е. односвязную цепь Маркова. В этом случае энтропия элемента xi определяться условной вероятностью p(xj / xi).

Для данного фиксированного xi энтропия сообщений будет определяться частной условной энтропией

( ⁄ ) = − ∑ ( ⁄ ) log2 ( ⁄ ) .

=0

Произведя усреднение по всем xi , получим выражение для средней энтропии сообщения

6

( ) = ∑ ( ) ( ⁄ ) =

=1

= − ∑ ( ) ∑ ( ⁄ ) log2 ( ⁄ ) =

=1 =1

=− ∑ ∑ ( ) log2 ( ⁄ ) .

=1 =1

При наличии коррелятивных связей между элементами энтропия сообщений, а следовательно, и количество передаваемой информации уменьшается, причем это уменьшение тем интенсивнее, чем сильнее коррелятивные связи и чем большее число элементов

элементами сообщения и когда все элементы алфавита вырабатываются с равными вероятностями. Очевидно, максимальная производительность источника полностью определяется размером алфавита М.

Для того чтобы характеризовать, насколько полно использует источник возможности алфавита, вводится параметр называемый избыточностью (коэффициентом избыточности), который определяется по следующей

На практике, удобно описывать работу Марковского

эргодиче ским, если вероятность перехода через произвольное большее некоторого фиксированного числа

т число шагов из каждого состояния si в произвольное

состояние sj больше нуля.

Если для некоторого эргодического Марковского источника с п состояниями известны только вероятности перехода из одного состояния в другое, то вероятности его состояний можно получить из системы уравнений

существуют) могут быть получены путем решения системы линейных алгебраических уравнений, которые получаются из дифференциальных уравнений Колмогорова, если приравнять производные к нулю, а вероятностные функции состояний P1(t), ..., Рn(t) в правых частях уравнений заменить соответственно на неизвестные финальные вероятности P1, ..., Рn.

Таким образом, для системы S с n состояниями получается система n линейных однородных алгебраических уравнений с n неизвестными P0, P1, ..., Рп, которые можно найти с точностью до произвольного множителя. Для нахождения точного значения P0, P1, ..., Рn к уравнениям добавляют нормировочное условие Р0 + P1 + ...+ Pn = 1, пользуясь которым можно выразить

8

любую из вероятностей Pi через другие и отбросить одно из уравнений.

Другим способом нахождения предельного состояния Марковской цепи является расчет цепи с учетом того, что цепь Маркова является регулярной. Это возможно, если выполняются следующие условия:

1. Предельная матрица вероятностей перехода существует.

П∞ = lim П .

→∞

Причем все n строк предельной матрицы представляют собой предельное распределение вероятностей состояний матрицы.

р∞

р∞ П∞ = ( ) .

р∞

2. Предельное распределение вероятностей состояний p∞ является единственным стационарным распределением вероятностей состояний любой

регулярной цепи Маркова p∞ = p0 .

3. Цепь Маркова везде будет регулярной, если существует некоторое натуральное значение шага n, при котором все компоненты некоторого столбца матрицы вероятностей перехода на этом шаге n, будет отлично от нуля. Другими словами, цепь Маркова является регулярной если, на некотором шаге n существует по меньшей мере одно состояние, которое может быть достигнуто из любого начального состояния.

9

Энтропия стационарного эргодического Марковского источника вычисляется исходя из того, что некоторое состояние источника Si является как бы подисточником без памяти, обладающим в свою очередь соответствующей энтропией. Тогда энтропия первоначального источника равна математическому ожиданию энтропии подисточников. Таким образом, стационарный эргодический Марковский источник с алфавитом из М символов, имеющий n состояний, т.е. N подисточников без памяти обладает энтропией, равной математическому оживанию энтропии подисточника.

N

H∞(X) = ∑ p∞H (X⁄Si),

i=1

где p∞ – предельное распределение вероятностей состояний.

Таким образом, при t→∞ в системе S устанавливается некоторый предельный стационарный режим: хотя система случайным образом и меняет свои состояния, но вероятность каждого из них не зависит от времени и каждое из состояний осуществляется с некоторой постоянной вероятностью, которая представляет собой среднее относительное время пребывания системы в данном состоянии. Это свойство позволяет обходиться при нахождении параметров системы на основе моделирования одной достаточно длинной реализацией.

Для вероятностей p1(t), p2(t),…, pn(t) можно составить систему линейных дифференциальных уравнений, называемых уравнениями Колмогорова, которые в случае нахождения предельных вероятностей превращаются в систему линейных алгебраических уравнений для каждого состояния. Совместно с нормировочным условием эти

10