Учебное пособие 1385

уравнения дают возможность вычислить все предельные вероятности.

Общее правило составления уравнений Колмогорова для предельных вероятностей pi(t) можно сформулировать следующим образом:

•в левой части уравнения стоит сумма произведений вероятностей всех состояний, из которых идут стрелки в i- ое состояние, на интенсивности соответствующих потоков минус сумма интенсивностей всех потоков, выводящих систему из данного (j-го) состояния, умноженная на вероятность данного (j-го) состояния;

•в правой части уравнения стоит 0.

Пример 1. Прогноз погоды.

Пусть а обозначает хорошую погоду, b – дождь, с – снег. Если сегодня хорошая погода, то завтра с равными вероятностями (согласно матрице переходных вероятностей) с равными вероятностями может быть хорошая погода, снег или дождь. Если, сегодня идет снег или дождь, то в половине случаев завтрашняя погода будет совпадать с сегодняшней, и на каждый из оставшихся прогнозов приходится лишь по одному шансу из четырех.

Матрицу переходных вероятностей можно изобразить в следующем виде:

Причем текущее состояние обозначается буквой слева от матрицы, а следующее состояние – буквой над матрицей. Сумма всех элементов любой строки матрицы

11

переходных вероятностей должна равняться 1, поскольку текущее состояние должно обязательно перейти в какое-то состояние.

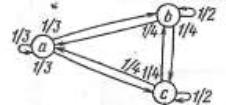
Удобно для наглядности процесса данную матрицу переходных вероятностей изобразить в виде графа переходов, представленных на рис. 3.

Рис. 3. Граф переходов

Предположим, что в качестве текущего (начального) состояния имеется вектор состояний (ра , рb , рс), где ра + рb

+ рс = 1.

Если известно, что сегодня хорошая погода (состояние а), т.е. ра = 1, тогда остальные возможные состояния будут иметь значения рb = рс = 0. Это означает, что текущее состояние точно определено.

В случае, если вектор начальных состояний нам не известен, то соответственно ра = рb = рс = 1/3.

Также, в общем случае, вектор начальных состояний может быть задан произвольным вектором значений.

Чтобы получить распределение вероятностей завтрашней погоды (в соответствии с уравнением Колмогорова-Чепмена) нужно умножить вектор-строку начальных состояний на матрицу переходных вероятностей:

12

Для нахождения вероятностей на 2 дня вперед нужно еще раз умножить этот вектор на матрицу переходных вероятностей. Поскольку умножение матриц (и векторов) ассоциативно, вместо этого можно сначала умножить матрицу переходных вероятностей на саму себя, получив квадрат матрицы, а затем умножить вектор начальных распределений на этот квадрат.

Квадрат матрицы переходных вероятностей равен:

Записывая матрицу в виде

Видим, что элементы квадрата матрицы переходных вероятностей меняются не сильно, как элементы первоначальной матрицы. Если возвести в квадрат эту матрицу, получим матрицу для предсказания погоды на 4 дня вперед. В частном случае несложно доказать, что последовательные степени матрицы переходных вероятностей сходятся к некоторой предельной матрице.

13

Рассчитаем распределение вероятностей состояний a, b, c для предельной матрицы (предельного состояния исследуемой системы). Для этого должно выполняться следующее равенство:

1⁄3 ( ) 1⁄4 1⁄2 1⁄4 = ( ).

(1⁄4 1⁄4 1⁄2)

Это эквивалентно системе из трех уравнений:

Для решения данной системы уравнений необходимо отбросить одно из уравнений и дополнить систему дополнительным условием

+ + = 1.

14

Решая полученную систему уравнений получаем следующее стационарное распределение

= 3⁄11 ; = 4⁄11 ; = 4⁄11.

Таким образом, независимо от первоначального распределения вероятностей для матрицы переходных вероятностей получаем предельное распределение вероятностей (3/11, 4/11, 4/11).

15

2. Энтропия источника сообщений

Получатель знает весь набор возможных сообщений, которые могут быть ему направлены, но какое именно сообщение передано ему сейчас – для него тайна. Именно в этом и заключается неопределенность состояния получателя. Если сообщение принято и есть уверенность, что понято правильно, то неопределенность исчезает. Другими словами сообщение содержало в себе ровно столько информации, сколько было неопределенности у получателя.

Таким образом, центральным вопросом становится способ определения меры неопределенности сообщения. Эта величина называется энтропией.

Если источник информации {Х, p(xi)}, i = 1,M, располагающий алфавитом из M букв, передал «случайно для себя» букву j , то количество переданной информации составит, согласно Шеннону, величину H (хj ) = - log2 p(хj). Чем больше вероятность p(хj), тем меньшее количество информации было передано.

Обычно в теории информации работают со средними значениями, поэтому источник принято характеризовать средней (больцмановской) энтропией, определяемой по формуле

Нср( ) = − ∑ ( ) ∙ log2 ( ) .

Можно показать, что средняя энтропия максимальна, если все сообщения равновероятны, т.е.

1

( ) = ; ( ) = log2 .

Если каждой паре xi yj поставлена в соответствие

16

вероятность p(xi yj), то имеем произведение ансамблей

{XY, p(xy)}. Для элементов объединенного ансамбля имеют место обычные свойства вероятностей:

∑ =1 ( , ) = ( ) , ∑ =1 ( , ) = ( ).

Из указанных свойств, в частности, следует, что если задано произведение ансамблей, то всегда могут быть найдены исходные ансамбли {X, p(x)} и {Y, p(y)}.

Обратное возможно лишь в случае, когда элементы исходных ансамблей независимы, при этом

p(xi yj) = p(xi )· p(yj ).

В общем случае для зависимых ансамблей p(xi yj) = p(xi) · p(yj / xi) = p(yj) · p(xi / yj),

т.е. для определения вероятности элемента объединенного ансамбля необходимо задание условной вероятности появления элемента одного из ансамблей, при условии, что реализовался элемент другого ансамбля:

( ⁄ ) = ( ) , ( ⁄ ) = ( ) .

( )

Математически канал связи задается множеством допустимых сообщений на входе, множеством допустимых сообщений на выходе и набором условных вероятностей P(y/x) получения сигнала y на выходе при входном сигнале x. Условные вероятности описывают статистические свойства “шумов” (или помех), искажающих сигнал в процессе передачи.

На практике чаще всего используется модель симметричного двоичного канала связи.

Схемы и матрицы основных симметричных каналов

17

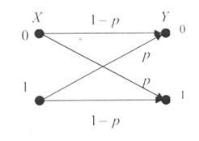
приведены на рис. 4, где р – вероятность трансформации сигнала; 1 - р - вероятность правильного прохождения сигнала.

Рис. 4. Схема и матрица двоичного симметричного канала связи

В реальных системах связи в результате искажений, которые возникают из-за шумов, действующих в канале связи, принятое сообщение отличается от переданного. Это означает, что в канале с шумами происходит потеря информации. Количество информации I(X) отражает свойство ненадежности системы.

Полную взаимную информацию ( ) можно определить исходя из начальных данных по следующим формулам:

В зависимости от условий поставленной задачи возможно найти все параметры системы, используя выше приведенные формулы.

Методы блочного кодирования, необходимые для решения данной задачи, приведены в следующей главе.

19