Учебное пособие 1344

Пример 6. Построить функцию эмпирического распределения.

В строке меню выберите Graphs/ Histograms. В открывшемся окне установите закладку Advanced. В новом окне выберите имя переменной с помощью

Variables. Далее установите Graph Type: Regulаr; Showing Type: Cumulative

(Накопление частоты), Fite Tуре(Подбираемый тип): Exponential (для нашего примера) или off (без подбора); Categories (Число интервалов группирова-

ния):250 - ОК.

Рис. 17

На экране - функция эмпирического распределения (с точностью до мелкого группирования с 250 интервалами).

Пример 7. Построить интервальный ряд (сгруппировать данные).

В строке меню: Statistics/Basic Statistics/Tables,- далее –Frequencies Tables задайте No. of exact intervals: 10 (10 интервалов группирования) или Step size: 2,- starting at: 0. Нажмите кнопку Summary, наблюдаемую панель выведите на печать или сохраните.

Задание к работе

1.Создать файл Primer.sta 1v*100c, содержащий выборку объема п=100, из индивидуальных заданий. Аналогично примерам 1-2 вычислить выборочные характеристики и построить гистограмму частот.

2.Открыть файл Gemat.sta. Аналогично примерам 3-4 построить диа-

грамму рассеяния и гистограмму двумерного распределения для любой пары переменных.

3.Для генерированной выборки (из файла Gener.sta) построить вариационный ряд, функцию эмпирического распределения, гистограмму частот.

4.Определить выборочные характеристики генерированной выборки. Сравнить выборочное среднее и стандартное отклонение с соответствующими теоретическими значениями, установленными при генерации выборки.

21

Лабораторная работа 6

ВЕРОЯТНОСТНЫЙ КАЛЬКУЛЯТОР

Цель работы – исследовать геометрический смысл и изучить способы построения таблиц модельных распределений.

Вероятностный калькулятор (Probability Calculator) запускается из стартовой панели модуля Basic Statistics and Tables (Основные статистики и таблицы).

Пример 1. Выяснить геометрический смысл параметров нормального распределения N(a; σ).

Положите а=0, σ=1. В окне Probability Distribution Calculator в поле

Distribution: выделите мышью строку Z(Normal), заполните поля: теап:0, sc. dev.:1, p:0,5. Поднимите флажок Fixed Scaling, далее нажмите кнопку Compute.

В поле X открытого окна появится значение .0000. Это 0.5 -квантиль нормального распределения, т.е. корень уравнения F(Z)=0.5. В поле Density Function изображается кривая распределения с заштрихованной областью. Площадь отмеченной области равна указанному значениюр=0,5. Выберите далееCreate Graph и нажмите кнопку Compute. На экране появится график плотности, с отмеченным синим пунктиром квантилем. Из графика видно, что 0.5 — квантиль – является модой и медианой нормального распределения. Повторяя приведенную последовательность команд для разных значений mean ( а=1; 2; -2;...), убедитесь, что значение а является точкой максимума функции плотности нормального распределения. (График плотности нормального распределения сдвигается по оси ординат при изменении среднего. При возрастании среднего графики сдвигаются вправо). Пик плотности нормального распределения находится в точке с ординатой, равной среднему значению.

Это значение задается в поле mean (среднее). Меняя значение поля sd.dev.(a) при постоянном а и р, убедитесь, что при увеличении а плотность нормального распределения рассеивается относительно a, fmax уменьшается. При уменьшении а плотность сжимается, концентрируясь возле точки максимума, fmax растет (рис. 18).

Рис.18

22

Пример 2. Вычислить вероятность Р(175<ζ<185) случайной величины , распределенной нормально с параметрами: а=176,6; σ=7,63.

В окне Probability Distribution Calculator заполните поля: Distribution: Z(Normal),:теап:176,6; sd.dev.:7,63; X:185 , далее нажмите кнопку Compute. В

поле р появится значение: 0.891022 - запомните его.

Измените значение X на 175, нажмите кнопку Compute. Запомните новое значение поля р:0.468661. Вычислите Р(175<ζ<185)=0.891022- 0.468661=0.422361≈0.4.

Правила 2- и 3-сигма

Пусть имеется нормально распределённая случайная величина ξ с математическим ожиданием, равным а, и дисперсией σ2. Определим вероятность попадания ξ в интервал (а- 3σ; а + 3σ), то есть вероятность того, что ξ принимает значения, отличающиеся от математического ожидания не более чем на три среднеквадратических отклонения.

Р(а- 3σ < ξ < а + 3σ)=Ф(3) - Ф(-3)=2Ф(3).

По таблице находим Ф(3)=0,49865, откуда следует, что 2Ф(3) практически равняется единице. Таким образом, можно сделать важный вывод: нормальная случайная величина принимает значения, отклоняющиеся от ее математического ожидания не более чем на 3σ.

(Выбор числа 3 здесь условен и никак не обосновывается: можно было выбрать 2,8, 2,9 или 3,2 и получить тот же вероятностный результат. Учитывая, что Ф(2)=0,477, можно было бы говорить и о правиле 2-х "сигм".)

Если от точки среднего или от точки максимума плотности нормального распределения отложить влево и вправо соответственно два и три стандартных отклонения (2- и 3- сигма), то площадь под графиком нормальной плотности, подсчитанная по этому промежутку, равна 95,45% и 99,73% всей площади под графиком. (Т.е. 95,45% и 99,73% всех независимых наблюдений лежит в радиусе 2-х и 3-х стандартных отклонений от среднего значения.)

Пример 3. Проверка правила 2-х и 3-х сигм. Проверить, что если Х~

N(a;σ), то Р(|Х-а|<2а) =0.9545, Р(|Х-а|<3σ) =0.9973 независимо от значений а и σ. В окне Probability Distribution Calculator в поле: Distribution: выделите Z(Normal).

Пометьте опцию Two-tailed (двухсторонний), т.к. неравенство с модулем является двухсторонним. Задайте meatuO, sd.dev. Поскольку 2а~2, в поле X поставьте 2, нажмите кнопку Compute.

В строке р появится число 0.954500, в поле Density Fипсtiоп (Функция плотности) заштрихованная площадь под графиком плотности составит 95,45% всей площади под графиком (рис. 19). Сделайте то же самое для 3σ. Убедитесь, что заштрихованная площадь достигнет 99,73%.

23

Рис. 19

Задавая различные значения а, σ, убедитесь, что правила 2-х и 3 -х сигм имеют место при любых значениях нормального распределения.

Пример 4. Вычислить 0.95 и 0.99 -квантили хи-квадрат распределения с 7 степенями свободы. Выяснить влияние числа степеней свободы на форму и расположение кривой распределения.

В окне Probability Distribution Calculator в поле: Distribution: выделите строку Chi. Заполните поля: df:7, p:0,95 - Compute. В поле Chi появится число:14.068419. Это 95% -я точка (.95 -квантиль), т.е. корень уравнения F(1)=0.95. Значит, Р(χ2≤14,068419)=0.95. Чтобы вычислить вероятность противоположного неравенства, поднимите флажок (1 -Cumulative p).

Поменяйте значение поля р: на 0.99 - Compute. В поле Chi появится число 18,477779. Это 99% - я точка (.99 - квантиль). Выберите опцию Create Graph—Compute. Вы построили график плотности и функции распределения хи-квадрат с 7 степенями свободы.

Задавая различные значения параметра k в поле df (2;5;12;...), убедитесь, что при увеличении k пик плотности распределения снижается и смещается вправо. График плотности становится более симметричным, приближаясь по форме к кривой Гаусса.

Пример 5. Выяснить влияние числа степеней свободы на форму и расположение кривой распределения Стьюдента.

В поле Distribution: выделите строку t (Student). Заполните поля: df: 5, р:,5. поле t система заполнит числом 0. Пометьте опцию Create Graph, далее нажмите Compute. Рассмотрите график и повторите алгоритм для df=10, 35, 50, 100. Убедитесь в том, что график плотности t -распределения симметричен относительно оси Оу и напоминает кривую Гаусса. С возрастанием числа степеней свободы k максимальное значение плотности увеличивается, хвосты более круто убывают к 0.

Вводя в поле р значения 0.5; 0.7; 0.95; 0.99, составьте таблицу значений

24

функции t –распределения с 10 степенями свободы (таблицу квантилей)(табл. 4).

Наоборот, введите в поле t значение 1. Система вычислит р: .829553.

Следовательно, P(t <1) =0.829553. Поднимите флажок (1 - Cumulative р).

Содержимое поля р изменится на.170447. Калькулятор вычислил вероятность противоположного события: P(t ≥1)=0.170447.

Пример 6. (Распределение Фишера). Убедитесь с помощью вероятностного калькулятора, что F- распределение сосредоточено на положительной полуоси. Определить 0.5 - и 0.75 -квантили F10,10 -распределения. Вычислить ве-

роятности P(F10,10 ≤1)u P(F10,10 ≤2).

В поле Distribution: выделите строку F. Заполните поля: р:,5; dfl:10; df2:10, далее нажмите Compute. Калькулятор вычислит значение поля F: 1. Поменяйте значение поля р:75. Значение поля F: изменится на 1,551256. Измените значение поля р: на 2, потом на 1. Калькулятор вычислит вероятности:

P(F10,10≤2)=0,144846 и P(F10,10 ≤1)=0,5.

Придавая различные значения df1 и df2, наблюдайте графики. Обратите внимание на то, что, в отличие от нормальной, криваяF-распределения несимметрична при небольших значениях степеней свободы(п и k<30). С возрастанием п и k кривая F-распределения медленно приближается к нормальной кривой.

Задание. Построить график плотности распределения Стъюдента с 5 степенями свободы. По уровню р:0.95 найдите значение t. Постройте график плотности распределения Стъюдента с 25 степенями свободы. Сравните графически плотность распределения Стьюдента с плотностью стандартного нормального распределения.

Биномиальное распределение и игровые задачи

Параметрами биномиального распределения являются вероятность успеха р (q=1-p) и число испытаний п. Вероятность m-успехов в п-испытаниях вычисляется по формуле

р(т;п)=В(т;п)*рт(1-р)п-т, m=0,l,...,n, B(m;n)=n!/((n-m)!*m!).

Создайте пустую электронную таблицу 1v*10c, назовите файл testsm.sta. Переменной VAR1 присвойте имя ВЕРОЯТ, в нижнем поле Long Name введите выражение, определяющее переменную: =Binom(v0,0.3,10) -OK.

Программа вычислит вероятность успеха и занесет их в таблицу в значения первой переменной. В данной таблице вероятность успеха – выпадения герба – равна 0,3. Из таблицы видно, что вероятность выпадения одного герба в 10 бросаниях- 0.12106, вероятность выпадения двух гербов в 10 бросаниях -

25

0.2334 и т.д.

Вероятность успеха легко изменить, сделав ее равной, например, 0.5. Это означает, что бросается симметричная монета и вероятность успеха равна вероятности неудачи. В поле Long Name достаточно изменить формулу, записав вместо 0.3 значение 0.5.

Если вы забыли функцию, вычисляющую биномиальные вероятности, в системе, то воспользуйтесь средством Function Browser. Нажав кнопку Functions в окне спецификации переменной, вы откроете диалоговое окно Function Browser, в котором в окне Category выберите Distributions, в окне Item выберите Binom. Нажмите Enter. Функция биномиального распределения появится в окне спецификации переменной в поле Long Name. Осталось только задать необходимые параметры и запустить вычисление. В дальнейшем нам понадобится вычислять не только биномиальные вероятности, но и биномиальные коэффициенты B(m;n). Это легко сделать, умножая биномиальные вероятности с вероятностью успеха р= 1/2 на 2 в степени п.

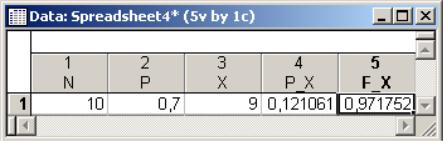
Выполним теперь расчеты для биномиального распределения с параметрами п=:10 и р=0.7 в точке х~9. Введем в таблицу заданные значения: N=10, Р=0.7, Х=9. Далее в окне спецификации четвертого столбца, названного Р_Х , в поле Long Name введем формулу для биномиального распределения =Binom(9;0,7;10)-OK. Аналогичным образом в окне спецификации для пятого столбца F_X введем формулу для функции биномиального распределения вида:

=IBinem(9;0,7;10) - OK.

Врезультатеполучимследующиеответы:Р{Х=9}=0.121; F(9)=0.972(рис.20).

Рис. 20

Рассчитаем далее распределение вероятностей и функцию распределения для множества точек х=0,1,2,..., 10 путем формирования 11 строк таблицы. В поле Long Name введем формулу для биномиального распределения

=Binom(v3;0,7;10)-OK. Далее в окне Displаy Format выберем опцию Number, а в окне Decimal places (количество точек после запятой)-5. Таблица с исходными данными и вычисленными результатами имеет следующий вид (рис. 21).

26

Рис. 21

Используя полученную таблицу, построим полигон вероятностей и функцию распределения для заданного биноминального распределения. Выберем

Graphs/2D Graphs/ Line Plot (Variables) и зададим имена переменных Р_Х и F_X. Установим Graph type:Multiple–OK (рис. 22).

Рис. 22

27

Задача шевалье де Мере

Однажды азартный игрок спросил, стоит ли ему ставить на выпадение двух шестерок одновременно при бросании двух костей 24 раза или нет?

Создайте рабочий файл play.sta. Дважды щелкните на имени переменной и откройте окно спецификации переменной varl. В п оле Lоng Name запишите формулу =Binom(v0,1/36,24), далее - ОК. Программа вычислит биномиальные вероятности. В первом столбце этой таблицы даны последовательно вероятности выпадения двух шестерок один раз, два разa, три раза и т.д. Нам нужно в ы- числить вероятность выпадения, по крайней мере, одной пары шестерок. Следовательно, все эти вероятности нужно сложить. Таким образом, вероятность выпадения, по крайней мере, одной пары шестерок при 24 бросаниях пары костей равна 0.49140. В длинной серии игр, состоящих из 24 бросаний пары костей, игрок, ставящий на выпадение двух шестерок одновременно, в среднем устойчиво проигрывает.

Вопрос: как изменить условия игры, чтобы находиться в выигрыше?

Изменённая задача шевалье де Мере

Предположим, что шевалье де Мере стал ставить на выпадение пары шестерок в 25 бросаниях.

Повторите все действия предыдущей задачи с переменной VAR2. В поле Long Name запишите формулу =Binom(v0,l/36,25), далее - ОК. Складывая значения во втором столбце, легко найти, что вероятность выпадения, по крайней мере, пары шестерок в 25 подбрасываниях пары костей больше 0.5.

Еще одна задача игрока.

Некогда один англичанин по имени С. Пепайес послал Ньютону письмо,

вкотором спрашивал, на что лучше ставить:

-на выпадение одной шестерки при бросании кости 6 раз?

-на выпадение двух шестерок при бросании кости 12 раз?

-на выпадение трех шестерок при бросании кости 18 раз?

-на выпадение четырех шестерок при бросании кости 24 раза? Используем по-прежнему файл play.sta. Увеличим его размеры, добавив

14 случаев (Cases - Add - 14. After case: 10) - ОК. Начнем с первого пари. Запишем биномиальные вероятности для первого пари в случае переменной VAR1. В поле Long Name запишите формулу =Binom(v0,l/6,6), далее - ОК. Далее то же самое для переменных VAR2, VAR3, VAR4, подставляя соответствующие вероятности для второго, третьего и четвертого пари.

В строке с номером i в данном файле дана вероятность выпадения i шестерок в первом, втором, третьем и четвертом пари. Суммируя значения вероятностей в столбцах, получим:

-0.665 для первого случая;

-0.619 для второго случая;

28

-0.597 для третьего случая;

-0.584 для четвертого случая.

Задание к работе

С помощью вероятностного калькулятора решите следующие задачи. 1. Задача о Гулливерах и лилипутах.

Представьте, что вы попали в страну, где рост взрослых мужчин приближенно имеет нормальное распределение со средним 176,6 см и стандартным отклонением 7,63 см. Какова вероятность, что случайно выбранный мужчина имеет рост больше 195 см, т.е. является Гулливером? Какова вероятность, что случайно выбранный мужчина имеет рост меньше 155 см, т.е. является лилипутом?

2.Для нормального распределения с выбранными параметрами вычислить вероятность попадания в интервал, содержащий mean и не содержащий mean.

3.Составить таблицы нормального, хи-квадрат, Стьюдента и Фишера распределений (по 10 значений). Вычислить 0,95 и 0,99 – квантили модельных распределений для различных значений параметра.

4.Проанализируйте влияние параметров распределения на форму кривых плотностей для следующих непрерывных распределений: экспоненциального, нормального Фишера, Стьюдента, хи -квадрат.

5.С помощью пакета STATISTICA проанализируйте влияние параметров распределения на форму полигона вероятностей для следующих, дискретных распределений: биномиального, Пуассона.

6.Решите задачу (генуэзская лотерея).

В генуэзской лотерее среди 90 номеров имеется ровно 5 выигрышных. Перед розыгрышем лотереи вы можете поставить любую сумму:

1)на любой из 90 номеров;

2)на любые два номера;

3)на любые три номера;

4)на любые четыре номера;

5)на любые пять номеров.

Вы выигрываете только в том случае, если поставили на 1, 7, 9 и все эти номера оказались среди выигрышных. Как обеспечить выигрыш?

Замечание. Вероятности вычисляются по следующей формуле:

Р(к)=В(k;5)/В(k;90), где В(k;5)=5!/(k!(5-k)!); В(k;90)=90!/(k!(90-k!)), k=1,2,3,4,5.

Лабораторная работа 7

ПРОВЕРКА СТАТИСТИЧЕСКИХ ГИПОТЕЗ. КРИТЕРИЙ СОГЛАСИЯ ХИ-КВАДРАТ ПИРСОНА

Цель работы – изучить способы проверок статистических гипотез, используя функции пакета STATISTICA.

Пусть Fθ = {F{x;θ),θ Θ } - заданное параметрическое семейство функ-

29

ций распределения (параметр θ или скалярный, или векторный) и Х = (Х,,Х2,...,Хп)- выборка из распределения L(ξ) с неизвестной функцией распреде-

ления. Требуется проверить гипотезу H0: L(ξ) Fθ . Статистика имеет вид

p j (θ) = P(ξ (z j −1, z j ) H0 ) - вероятности исходов, которые представляют собой

некоторые функции от неизвестного параметра θ; θ =θn - оценка максимального правдоподобия для θ.

то гипотеза Н0 отклоняется.

Проверка гипотез о законе распределения

Пример 1. Проверка гипотезы о нормальном законе распределения размеров головок заклепок, сделанных на одном станке, по выборке объема n=200; измерения приведены в таблице лабораторной работы № 5.

Откройте или создайте заново файл Diamz.sta. В модуле Statistics выберите Distribution Fitting (подбор распределений). В поле Continuous Distributions: Normal – OK. Установите имя переменной с помощью Variable, затем нажмите кнопку Plot of observed and expected distribution. Получим графическое представление значений наблюдаемых и ожидаемых частот.

Вернитесь в окно Fitting Continuous Distributions, выберите закладку Parameters, а затем нажмите на кнопку Summary. Число групп Number of Categories: 13 - OK.

В таблице частот нужны столбцы observed frequency (наблюдаемыe частоты) и expected frequency(ожидаемыe частоты), а также столбец разности - observed expected. В таблице приведено значение статистики χ2 (Chi-Square): 159.21, количество степеней свободы df=1. Приведено значение вероятности p=P{ χ2≥12}=0.000007.

Последнее равенство означает, что если гипотеза верна, вероятность поручить значение Х2 ≥ 12.000 равна 0.000007. Это слишком малая вероятность, поэтому отклоняем гипотезу о нормальности.

Посмотрим гистограмму наблюдений (или гистограмму рассеяния): Griphs —— Histograms - ... -ОК. Видим, что в выборке d2 имеется одно ано-

30