
- •Preface
- •Contents
- •1 Introduction
- •References
- •2.1…Review of Dynamic Engineering Theories of Thin-Walled Beams of Open Section
- •References
- •3.1…Theory of Thin-Walled Beams Based on 3D Equations of the Theory of Elasticity
- •3.1.1 Problem Formulation and Governing Equations
- •3.1.2.1 Solution on the Quasi-Longitudinal Wave
- •3.1.2.2 Solution on the Quasi-Transverse Shear Wave
- •3.2…Construction of the Desired Wave Fields in Terms of the Ray Series
- •References
- •4.2.3 Numerical Example
- •Appendix
- •References
- •5 Conclusion
- •6.3…The Main Kinematic and Dynamic Characteristics of the Wave Surface
- •Reference
Chapter 3
Transient Dynamics of Pre-Stressed
Spatially Curved Thin-Walled Beams
of Open Profile
Abstract The dynamic stability with respect to small pertubations, as well as the local damage of geometrically nonlinear elastic spatially curved open section beams with axial precompression have been analyzed. Transient waves, which are the surfaces of strong discontinuity and wherein the stress and strain fields experience discontinuities, are used as small pertubations, in so doing the discontinuities are considered to be of small values. Such waves are initiated during low-velocity impacts upon thin-walled beams. The theory of discontinuities and the method of ray expansions, which allow one to find the desired fields behind the fronts of the transient waves in terms of discontinuities in time-derivatives of the values to be found, are used as the methods of solution for short-time dynamic processes.
Keywords Pre-stressed spatially curved thin-walled beam of open section Small transient perturbations Surfaces of strong discontinuity Recurrent equations of the ray method Ray expansions
3.1Theory of Thin-Walled Beams Based on 3D Equations of the Theory of Elasticity
For investigating the dynamic behaviour of thin-walled beams of open section, we shall proceed from three-dimensional (3D) equations of isotropic elasticity written in the Cartesian system of coordinates x1; x2; and x3:
3.1.1 Problem Formulation and Governing Equations
Let us consider a certain unperturbed equilibrium of an elastic body characterized by the displacement vector u0i ; stress tensor r0ij; and the vector of volume forces Xi0
Y. A. Rossikhin and M. V. Shitikova, Dynamic Response of Pre-Stressed Spatially |
19 |
Curved Thin-Walled Beams of Open Profile, SpringerBriefs in Applied Sciences and Technology, DOI: 10.1007/978-3-642-20969-7_3, Yury A. Rossikhin 2011

20 |
3 Transient Dynamics of Pre-Stressed Spatially Curved Thin-Walled Beams |
(surface forces are absent). The characteristics of the unperturbed equilibrium state satisfy the following geometrically nonlinear equations and boundary conditions on the surface [1]:
frjk0 ðdik þ ui0;kÞg; j þ Xi0 ¼ 0; |
ð3:1Þ |
rjk0 ðdik þ ui0;kÞmj ¼ 0; |
ð3:2Þ |
where dik is the Kronecker’s symbol, mj are the components of the unit vector normal to the boundary surface, Latin indices take on the magnitudes 1, 2, 3, a Latin index after comma denotes the partial derivative with respect to the corresponding spatial coordinate x1; x2; x3; and the summation is understood over the repeated indices.
Let us perturb the body with some small deviations from the unperturbed equilibrium: ui; rij; Xi ¼ q€ui; where q is the material density, and an overdot
denotes the time-derivative. The |
characteristic |
components of |
the perturbed |
|
e |
|
|
|
|
motion eui; reij; and Xi take the form |
|
|
|
|
0 |
0 |
þ rij; |
e |
ð3:3Þ |
eui ¼ ui þ ui; |
reij ¼ rij |
Xi ¼ qvi; |
||
where vi is the displacement velocity.
The components of the perturbed state satisfy the following equations and
boundary conditions: |
|
|
|
|
|
|
|
¼ 0; |
|
reikðdik þ eui;kÞ |
|
e |
ð3:4Þ |
|
|
; j þ Xi |
|||
|
|
|
|
ð3:5Þ |
rejk dik þ eui;k mj ¼ 0: |
||||
Substituting (3.3) in (3.4) and (3.5), carrying out the linearization of the
resulting equations, and taking (3.1) and (3.2) into account, we find |
|
|||
n |
|
|
o |
|
rjk dik þ ui0;k |
|
þ rjk0 ui;k ; j¼ q€ui; |
ð3:6Þ |
|
n |
|
|
o |
|
|
rjk dik þ ui0;k |
þ rjk0 ui;k mj ¼ 0: |
ð3:7Þ |
|
Suppose that the unperturbed state deviates a little from the initial undeformed state. In the majority of engineering problems the given assumption is found to be valid. In this case, the terms u0i;k can be neglected, and Eqs. 3.2, 3.6 and 3.7 at r0ij ¼ cij; where cij ði; j ¼ 1; 2; 3Þ are certain constant values (moreover, some of them could be vanished according to the conditions of the problem under consideration), take the following form:
rij; j þ rjl0 ui;lj ¼ qvi; |
ð3:8Þ |
rijmj ¼ 0; |
ð3:9Þ |

3.1 Theory of Thin-Walled Beams Based on 3D Equations |
21 |
Fig. 3.1 Scheme of a spatially curved linear elastic beam of arbitrary open cross-section
rij0 mj ¼ 0: |
|
ð3:10Þ |
Equations 3.8–3.10 should be considered together with the relationship |
|
|
|
|
ð3:11Þ |
rij ¼ kvl;ldij þ l vi; j þ vj;i ; |
||
where k and l are Lame constants.
Suppose that the wave surface of strong discontinuity exists in a spatially curved thin-walled beam of open section. Then let us differentiate (3.8), (3.11) and (3.9) k times with respect to time, write them on the both sides of the wave surface, and take their difference. As a result we obtain
|
|
|
|
|
|
|
ð3:12Þ |
rij;ðkþ1Þ ¼ k vl;lðkÞ dij þ l vi; jðkÞ þ vj;iðkÞ |
; |
||||||
|
|
|
|
|
|
|
ð3:13Þ |
rij;jðkÞ þ rjl0 eil; jðk 1Þ ¼ q vi;ðkþ1Þ ; |
|
||||||
|
|
|
|
|
|
|
ð3:14Þ |
|
rij;ðkÞ mj ¼ 0; |
|
|
||||
|
|
|
|
|
|
|
|
where eij ¼ vi;j; and Z;ðkÞ |
¼ okZ=otk |
|
þ |
okZ=otk |
: |
|
|
Equation 3.13 lacks the discontinuities in the external forces, since they are continuous on the wave surface of strong discontinuity.
For the ease of further treatment, let us introduce two sets of coordinates:
k; s; n with the unit vectors kfkig; sfsig; and nfnig; and k; x, y with the unit vectors k; kfkig; and sfsig: The axes k; s; n are the natural axes for the curved axis
of the beam, in so doing the k-axis is the tangent to the beam’s axis, the s-axis is its binormal, the n-axis is its main normal, s is the arc length calculated from a certain point with the coordinate s0 along the beam axis (Fig. 3.1), while the x- and y-axes are the main central axes of the beam’s normal section. The angle uðsÞ is the angle between the x- and s-axes and the y- and n-axes.

22 |
3 Transient Dynamics of Pre-Stressed Spatially Curved Thin-Walled Beams |
|||||||
|
Following [2], it can be shown that (for details see Appendix 1) |
|
||||||
|
|
|
|
dsi |
¼ kiðK þ sÞ ki cos uðsÞ; |
ð3:15Þ |
||
|
|
|
|
ds |
||||
|
|
|
dki |
¼ siðK þ sÞ þ ki sin uðsÞ; |
ð3:16Þ |
|||
|
|
|
|
|
|
|||
|
|
|
ds |
|||||
|
|
dki |
|
|
||||
|
|
|
¼ ki sin uðsÞ þ si cos uðsÞ; |
ð3:17Þ |
||||
|
|
ds |
||||||
where K ¼ du=ds; while ðsÞ and sðsÞ are the curvature and the torsion of the beam’s axis, respectively. Note that it is precisely these three values, K(s), ðsÞ and sðsÞ; that are of prime engineering interest in studying the spatially curved thin-walled beams of open profile. Moreover, as it will be shown in the further analysis, these values produce new features in the dynamic response of such beams as compared with straight thin-walled beams of open cross-section.
Considering the conditions of compatibility (see Sect. 6.1)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d½rij;ðkÞ& |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
G 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
o rij;ðkÞ |
k |
|
|
o½rij;ðkÞ& |
s |
|
; |
|
|
|
|
3:18 |
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
þ |
|
ð |
Þ |
||||||||||||||||||||||||||||||||||||||||||||
rij; jðkÞ ¼ |
|
|
|
rij;ðkþ1Þ kj þ |
|
|
ds |
|
|
kj þ |
|
|
ox |
|
|
|
|
j |
|
|
|
oy |
|
|
|
j |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d½eil;ðkÞ& |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
o eil;ðkÞ |
|
|
|
|
o eil;ðkÞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
e |
il; jðkÞ |
¼ |
G 1 e |
|
|
|
|
|
|
|
|
|
|
|
kj þ |
|
k |
|
|
s |
; |
|
|
|
ð |
3:19 |
Þ |
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
il;ðkþ1Þ kj þ |
|
|
ds |
|
|
|
|
|
ox |
|
|
|
|
j þ |
|
|
oy |
|
|
|
j |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d vi;ðkÞ |
|
|
|
|
|
o vi;ðkÞ |
|
|
|
o vi;ðkÞ |
|
|
|
|
|
||||||||||||||||||||||
e |
|
|
¼ |
v |
i;lðkÞ |
|
|
|
|
|
|
|
G 1 v |
i;ðkþ1Þ kl þ |
|
|
|
|
|
|
k |
l þ |
s ; |
|
|
|||||||||||||||||||||||||||||||||||||||||||
il;ðkÞ |
|
|
|
¼ |
|
|
|
|
|
|
|
|
|
ds |
|
|
kl þ |
|
|
ox |
|
|
|
|
|
|
|
|
oy |
|
|
l |
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ð3:20Þ |
|||||
as well as formulas (3.15)–(3.17), Eqs. 3.12 and 3.13 can be rewritten as |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
r |
ij;ðkþ1Þ |
¼ |
G 1 |
|
|
|
v |
l;ðkþ1Þ |
l |
d |
ij |
|
G 1 |
l |
|
v |
|
|
|
|
kj |
|
|
v |
j;ðkþ1Þ& |
ki |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
k½ |
|
&k |
|
|
|
|
|
|
½ |
|
|
i;ðkþ1Þ& |
þ ½ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
þ k |
|
d½vl;ðkÞ& |
kl |
þ |
o½vl;ðkÞ& |
k |
|
|
|
|
o½vl;ðkÞ&s |
|
|
|
dij |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
ds |
|
|
|
|
|
ox |
|
|
|
|
l þ |
|
|
oy |
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
d½vi;ðkÞ& |
kj þ |
d½vj;ðkÞ& |
|
|
|
|
|
o½vi;ðkÞ&k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
þ l |
|
|
|
|
ds |
|
|
|
|
|
ds |
|
|
|
ki þ |
|
|
ox |
|
|
j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
o½vj;ðkÞ& |
k |
|
|
|
o½vi;ðkÞ& |
s |
|
|
|
|
o½vj;ðkÞ&s |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
21 |
|
||||||||||||||||||||
|
|
|
|
|
|
þ |
|
|
|
|
|
þ |
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ð |
: |
Þ |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
ox |
|
|
|
|
i |
þ |
oy |
|
|
|
j |
|
|
|
oy |
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
v |
|
|
|
|
G 1 |
½rij;ðkþ1Þ&kj þ |
d½rij;ðkÞ& |
|
|
|
|
o½rij;ðkÞ&k |
|
o½rij;ðkÞ& |
s |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
q½ |
i;ðkþ1Þ& ¼ |
|
|
|
|
|
|
ds |
|
|
kj þ |
|
|
ox |
|
|
j þ oy |
|
|
|
|
|
|
j |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
þ |
|
G 2 |
v |
|
|
|
|
|
0 |
|
|
|
|
2G 1d½vi;ðkÞ& |
|
0 |
|
2G 1 |
o½vi;ðk 1Þ |
& |
0 |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
½ |
|
|
i;ðkþ1Þ&rkk |
|
|
|
|
d2 |
|
|
|
|
ds |
|
rkk |
|
|
|
|
|
|
|
|
ox |
|
|
|
|
|
|
rkx |
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
2G 1 |
o½vi;ðk 1Þ& |
0 |
|
|
|
|
|
½vi;ðk 1Þ |
& |
|
0 |
|
|
|
|
2 |
o |
|
d½vi;ðk 1Þ |
& |
|
0 |
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
rkk |
þ |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
oy |
rky þ |
|
|
|
|
ds2 |
|
|
|
|
|
ox |
|
|
|
|
ds |
|
|
|
|
|
|
|
rkx |
|
|
|
|
|||||||||||||||||||||||

3.1 Theory of Thin-Walled Beams Based on 3D Equations |
|
|
|
|
|
|
|
|
23 |
|||||||||||||||||||||
|
2 o |
d½vi;ðk 1Þ& |
|
0 |
o½vi;ðk 1Þ& |
n |
|
|
K |
|
0 |
|
0 |
|
sin |
o |
|
|
|
|||||||||||
þ |
rky þ |
ð |
þ sÞrky þ rkk |
u |
|
|
|
|||||||||||||||||||||||
oy |
|
|
ds |
|
|
|
|
ox |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
o½vi;ðk 1Þ& |
|
K |
|
|
0 |
|
0 |
|
cos |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
þ |
þ sÞrkx |
rkk |
u |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
oy |
|
|
ð |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
G 1 |
|
v |
|
|
|
|
d½vi;ðk 1Þ& |
|
|
0 sin |
|
|
0 |
cos |
|
; |
|
|
|
|
|
3:22 |
|
|||||
þ |
|
½ |
i;ðkÞ& |
|
u |
rky |
u |
|
|
|
|
ð |
Þ |
|||||||||||||||||
|
|
|
|
|
ds |
|
|
rkx |
|
|
|
|
|
|
|
|
||||||||||||||
where rkk0 |
¼ rij0 kikj; rk0x |
¼ rij0 kikj; and rk0y |
¼ rij0 kisj: |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
Analysis of the influence of the preliminary shear stresses r0 |
and r0 |
and the |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
kx |
|
ky |
|
|
|
|
axial compression or tension stresses r0kk and their different combinations on the dynamic response of thin-walled rods of open profile is a very complicated problem which is of great importance in civil engineering and bridge construction.
However, reference to Eq. 3.22 shows that the value r0kk is multiplied by the k ? 1-order jump and by the s-derivative of the k-order, i.e. it has a strong impact both on the velocities of the surfaces of strong discontinuity and on the discontinuities, in contrast to the values r0kx and r0ky which are multiplied only by the k- and k - 1-order jumps, i.e. they exert weak effect only on the jumps. That is why, below in Sect. 3.1.2 , we shall neglect r0kx and r0ky with respect to the value r0kk:
3.1.2Dynamic Response of Axially Pre-Stressed Spatially Curved Thin-Walled Beams of Open Profile
Thus, assuming further that r0kx ¼ r0ky ¼ 0 and r0kk 6¼ 0; from (3.22) we have
q½ |
v |
G 1 |
½rij;ðkþ1Þ&kj þ |
d½rij;ðkÞ& |
kj þ |
o½rij;ðkÞ& |
k |
o½rij;ðkÞ& |
s |
|
|
|
||||||||||||
i;ðkþ1Þ& ¼ |
|
|
ds |
|
ox |
|
j þ |
|
oy |
j |
|
|
||||||||||||
|
þ |
G 2 |
½ |
v |
i;ðkþ1Þ& |
2G 1 |
d½vi;ðkÞ& |
d2 |
½vi;ðk 1Þ |
& |
|
o½vi;ðk 1Þ& |
sin |
u |
||||||||||
|
þ |
|||||||||||||||||||||||
|
|
|
|
|
|
|
ds |
|
ds2 |
þ |
|
|
ox |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
o½vi;ðk 1Þ& |
cos |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
u |
rkk: |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
oy |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ð3:23Þ |
|
To satisfy Eq. 3.14, it is sufficient to put |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ð3:24Þ |
||
|
|
|
|
|
|
|
|
rij;ðkÞ kikj ¼ 0; |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ð3:25Þ |
||
|
|
|
|
|
|
|
|
rij;ðkÞ sisj ¼ 0; |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ð3:26Þ |
||
|
|
|
|
|
|
|
|
rij;ðkÞ sikj ¼ 0: |
|
|
|
|
|
|
|
|
||||||||
24 |
3 Transient Dynamics of Pre-Stressed Spatially Curved Thin-Walled Beams |
Fig. 3.2 Scheme of the cross section of a thin-walled beam with a generic open crosssection
Then the boundary surface will be free from the normal and tangential stresses. Now we expand the value ½vi;ðkÞ& entering into (3.21) and (3.23)–(3.26) in terms
of three mutually orthogonal vectors k; k, s. As a result we obtain
vi;ðkÞ ¼ xðkÞki þ hðkÞki þ gðkÞsi; |
ð3:27Þ |
where xðkÞ ¼ ½vi;ðkÞ&ki; hðkÞ ¼ ½vi;ðkÞ&ki; and gðkÞ ¼ ½vi;ðkÞ&si:
Suppose that for a thin-walled beam of open section the following velocity fields (involving seven independent functions at each fixed k) are fulfilled [3]:
0 |
e1x |
e1y |
e |
Þ; |
ð3:28Þ |
xðkÞ ¼ xðkÞðs; s1Þ ¼ xðkÞ |
ðsÞþ xðkÞ |
ðsÞyðs1Þþ xðkÞ |
ðsÞxðs1Þþ wðkÞxAðs1 |
||
hðkÞ ¼ hðkÞðs; s1Þ ¼ hð0kÞðsÞ xð1kkÞðsÞðyðs1Þ ayÞ; |
|
ð3:29Þ |
|||
gðkÞ ¼ gðkÞðs; s1Þ ¼ gð0kÞðsÞ þ xð1kkÞðsÞðxðs1Þ axÞ; |
|
ð3:30Þ |
|||
where s1 is the arc length measured along the cross-section profile from the point M0; which corresponds to the arc length of s01; to the point M½xðs1Þ; yðs1Þ&; which corresponds to the arc length of s1 (Fig. 3.2).
Gol’denveizer [3] proposed that the angles of in-plane rotation do not coincide with the first derivatives of the lateral displacement components and, analogously, warping does not coincide with the first derivative of the torsional rotation. Thus Gol’denveizer [3] pioneered in combining Timoshenko’s beam theory [4] and Vlasov thin-walled beam theory [5] and suggested to characterize the displacements of the thin-walled beam’s cross-section by seven generalized displacements.
In order to refine the structure of formula (3.28) in the case of a spatially curved thin-walled beam, let us differentiate (3.27), which involves only the terms x0ðkÞ; h0ðkÞ; and g0ðkÞ; with respect to s with due account for (3.15)–(3.17). As a result we obtain

3.1 Theory of Thin-Walled Beams Based on 3D Equations |
25 |
|
|
0 |
|
dx0 |
|
|
|
|
|
! |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
||||
d v |
iðkÞ |
|
|
0 |
|
0 |
|
|
|
|
||||
|
|
|
|
ðkÞ |
|
|
|
|
|
|
||||
ds |
|
¼ |
|
ds |
þ hðkÞ |
sin u gðkÞ |
cos u ki |
|
|
|||||
|
|
|
|
|
|
dhð0kÞ |
|
|
|
|
! |
|
||
|
|
|
|
|
|
|
0 |
|
0 |
ðK þ sÞ |
ki |
|
||
|
|
|
þ |
|
|
xðkÞ |
sin u þ gðkÞ |
|
||||||
|
|
|
|
ds |
|
|||||||||
|
|
|
|
|
|
dg0 |
|
|
|
|
|
! |
|
|
|
|
|
|
|
|
|
0 |
|
0 |
|
|
|
||
|
|
|
|
|
|
|
ðkÞ |
|
|
|
|
ð3:31Þ |
||
|
|
|
þ |
|
|
þ xðkÞ |
cos u hðkÞðK þ sÞ |
si: |
||||||
|
|
|
|
ds |
||||||||||
Moreover, we shall use the relationship for the discontinuity in the k-order derivative with respect to time t of the angular velocity
|
1k |
e1x |
e1y |
|
|
ð3:32Þ |
|||
|
XiðkÞ ¼ xðkÞki þ xðkÞki þ xðkÞsi: |
|||
Differentiating (3.32) with respect to s and considering (3.15)–(3.17) yields
|
|
dxð1kkÞ |
|
|
|
|
|
|
|
|
|
! |
|
|
||
d½XiðkÞ& |
¼ |
|
e1x |
|
sin |
e1y |
|
cos |
u ki |
|
|
|||||
ds |
|
ds |
þ xðkÞ |
|
|
u xðkÞ |
|
|
|
|
||||||
|
|
|
|
e1x |
|
|
|
|
|
|
|
|
! |
|
||
|
|
|
|
|
1k |
|
e1y |
|
|
|
|
|||||
|
|
|
|
dxðkÞ |
|
|
ðK þ sÞ |
ki |
|
|||||||
|
þ |
|
ds |
xðkÞ |
sin u þ xðkÞ |
|
||||||||||
|
|
|
|
e1y |
|
|
|
|
|
|
|
|
|
! |
|
|
|
|
|
|
|
1k |
|
e1x |
|
|
|
|
|||||
|
|
|
|
dxðkÞ |
|
|
|
|
|
ð3:33Þ |
||||||
|
þ |
|
ds |
þ xðkÞ |
cos u xðkÞðK þ sÞ |
si: |
||||||||||
If we suppose that transverse shear strains are absent, then we are led to the following relationships, which are in compliance with the Vlasov theory:
|
|
|
|
|
|
|
dg0 |
|
|
|
|
! |
|
||
e1x |
|
|
|
|
|
0 |
|
0 |
|
|
|
||||
|
|
|
|
|
|
ðkÞ |
|
|
|
|
|
||||
xðkÞ |
¼ |
|
|
ds |
þ xðkÞ cos u hðkÞðK |
þ sÞ |
; |
ð3:34Þ |
|||||||
|
|
|
|
|
|
|
dhð0kÞ |
|
|
|
! |
|
|||
e1y |
|
|
|
|
|
0 |
|
0 |
|
|
|
||||
xðkÞ |
¼ |
|
|
|
|
xðkÞ sin u þ gðkÞðK |
þ sÞ |
; |
ð3:35Þ |
||||||
|
ds |
||||||||||||||
|
|
|
dx1k |
|
|
|
|
|
|
! |
|
|
|||
|
|
|
|
e1x |
e1y |
|
|
|
|||||||
e |
|
ðkÞ |
|
|
|
|
|||||||||
wðkÞ ¼ |
|
ds |
|
|
þ xðkÞ sin u xðkÞ cos u |
|
|
|
|||||||
|
dx1k |
|
|
|
dg0 |
|
dh0 |
|
|
|
|
||||
¼ |
|
|
ðkÞ |
|
þ |
|
ðkÞ |
sin u |
ðkÞ |
cos u |
|
|
|
||
|
ds |
|
ds |
ds |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ð3:36Þ |
þ xð0kÞ 2 sin u hð0kÞ sin u þ gð0kÞ cos u ðK þ sÞ: |
|||||||||||||||
If we now substitute (3.34)–(3.36) in (3.28), then we obtain a formula for defining the k-order time-derivative in the discontinuity in the velocity of translation along the k-axis without account for transverse shear deformations.
26 3 Transient Dynamics of Pre-Stressed Spatially Curved Thin-Walled Beams
Following Gol’denveizer [3], in order to take the transverse shear deformations
into account, it is essential to substitute the derivatives dx1k |
=ds; dg0 |
=ds; and |
|||||||
|
|
|
|
|
|
|
ðkÞ |
ðkÞ |
|
dh0 |
=ds by the independent functions w |
ðkÞ |
; x1x ; and x1y ; respectively, i.e. to |
||||||
ðkÞ |
|
|
|
|
ðkÞ |
ðkÞ |
|
|
|
rewrite Eqs. 3.34–3.36 as |
|
|
|
|
|
|
|
||
|
xeð1kxÞ |
|
|
|
|
|
|
|
|
|
¼ xð1kxÞ þ xð0kÞ cos u hð0kÞðK þ sÞ ; |
ð3:37Þ |
|||||||
|
e1y |
|
|
|
|
|
|
|
|
|
1y |
0 |
|
|
0 |
þ sÞ ; |
ð3:38Þ |
||
|
xðkÞ |
¼ xðkÞ |
xðkÞ sin u |
þ gðkÞðK |
|||||
|
|
|
|
|
|
|
|
|
|
|
e |
e1x |
|
e1y |
cos u |
|
|
|
|
|
wðkÞ ¼ wðkÞ þ xðkÞ |
sin u xðkÞ |
|
|
|
||||
|
¼ wðkÞ þ xð1kxÞ sin u xð1kyÞ cos u |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
ð3:39Þ |
|
þ xð0kÞ 2 sin u hð0kÞ sin u þ gð0kÞ cos u ðK þ sÞ: |
||||||||
As a result, instead of formula (3.28), we obtain |
|
|
|
||||||
xðkÞðs; s1Þ ¼ xð0kÞðsÞ |
h |
|
|
|
|
i |
|
|
|
xð1kxÞðsÞ þ xð0kÞ cos u hð0kÞðK þ sÞ yðs1Þ |
|
||||||||
|
h |
|
|
|
|
i |
|
|
|
|
xð1kyÞðsÞ xð0kÞ sin u þ gð0kÞðK þ sÞ xðs1Þ |
|
|
||||||
|
h |
|
|
|
|
|
|
|
|
|
þ wðkÞðsÞ þ xð1kxÞðsÞ sin u xð1kyÞðsÞ cos u þ xð0kÞ 2 sin 2u |
||||||||
|
|
|
|
|
|
i |
|
|
ð3:40Þ |
|
hð0kÞ sin u þ gð0kÞ cos u ðK þ sÞ xAðs1Þ: |
|
|||||||
Formulas (3.29) and (3.30) remain unchanged.
If we put K ¼ ¼ s ¼ 0 in (3.40), then we are led to the case of a straight thin-
walled rod of open profile. |
|
|
|
|
In further treatment we will use formulas (3.28)–(3.30), |
but |
in |
the |
final |
e |
e |
1x |
; and |
e1y |
relationships we will carry out the substitution of the values wðkÞ; x k |
x k |
|||
|
|
ð Þ |
|
ð Þ |
by their magnitudes defined by formulas (3.37)–(3.39).
At k ¼ 0; the values entering in (3.29), (3.30) and (3.40) have the following physical meaning: x0ð0ÞðsÞ; h0ð0ÞðsÞ and g0ð0ÞðsÞ are the discontinuities in the velocities of translatory motion of the section as a rigid body together with the point C (the center of gravity of the cross-section) along the k-, x- and y-axes, respectively, x1ð0xÞðsÞ; x1ð0yÞðsÞ and x1ð0kÞðsÞ are the discontinuities in the angular velocities of the cross-section’s rotation as a rigid whole around the x-, y- and k-axes, respectively, wð0ÞðsÞ is the discontinuity in the velocity of warping of the cross section, xAðs1Þ is twice the area of the sector AM0M; the point A is the center of bending (Fig. 3.2) with the coordinates [5]

3.1 Theory of Thin-Walled Beams Based on 3D Equations |
27 |
|
1 |
Z |
|
1 |
Z |
|
|
ax ¼ |
|
xCðs1Þyðs1ÞdF; |
ay ¼ |
|
xCðs1Þxðs1ÞdF: |
ð3:41Þ |
|
Ix |
Iy |
||||||
|
|
F |
|
|
|
F |
|
Since the section is referred to the main central axes, then |
|
||||||
Z |
|
|
Z |
|
|
Z |
|
Ixy ¼ xðs1Þyðs1ÞdF ¼ 0; |
Sy ¼ xðs1ÞdF ¼ 0; Sx ¼ yðs1ÞdF ¼ 0: |
||||||
F |
|
|
F |
|
|
F |
ð3:42Þ |
|
|
|
|
|
|
|
|
Moreover, the choice of the point A with the coordinates defined by formulas (3.41) results in the fulfillment of the following relationships:
Z |
Z |
|
Ixx ¼ xðs1ÞxAðs1ÞdF ¼ 0; |
Ixy ¼ yðs1ÞxAðs1ÞdF ¼ 0: |
ð3:43Þ |
F |
F |
|
Note that the sectorial area, generally speaking, depends on two coordinates, namely: the initial point s01 and the terminal point s11; i.e. xAðs01; s11Þ: Let us choose
s1 |
in such a way that the relationship |
|
|
|
1 |
|
|
|
|
|
|
1 Z |
|
|
|
xAðs10; s11Þ ¼ |
|
xAðs10; s1ÞdF |
ð3:44Þ |
|
F |
|||
F
will be valid. Then, as it is shown in [5], taking the point with the coordinate s11 as
the origin of the arc length measuring, we obtain
Z
Sx ¼ xAðs11; s1ÞdF ¼ 0: |
ð3:45Þ |
F |
|
Let us name this point as the null sectorial point [5]. Since there may exist several such points, the null sectorial point nearest to the point A can be named as the main null sectorial point, and we shall take it as the initial point of reading.
Thus, using the above mentioned choice of the coordinates and the initial points of measuring, the functions 1, xðs1Þ; yðs1Þ; and xAðs11; s1Þ; as formulas (3.42)– (3.45) show, occur to be orthogonal.
If we substitute (3.21) in (3.24) and (3.25) and consider (3.27), then we are led
to the relationships |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
k |
|
|
|
|
|
dxðk 1Þ |
|
|
|
|
|
|
|
|
|
|
|
|
||
½ex;ðkÞ& ¼ ½ey;ðkÞ& ¼ |
|
|
G 1 |
xðkÞ |
þ |
|
gðk 1Þ |
cos |
u |
|
sin |
u |
; |
||||||||
2ðk þ lÞ |
ds |
||||||||||||||||||||
|
|
|
|
hðk 1Þ |
|
|
|||||||||||||||
where |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ð3:46Þ |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
½ex;ðkÞ& ¼ |
o ½vi;ðk 1Þ&ki |
|
; |
½ey;ðkÞ& ¼ |
o ½vi;ðk 1Þ&si |
|
: |
|
|
|
|
||||||||||
|
|
ox |
|
|
oy |
|
|
|
|
|
|
||||||||||
Equation 3.26, after the substitution of (3.21), (3.27), (3.29), and (3.30) in it, is fulfilled unconditionally.

28 3 Transient Dynamics of Pre-Stressed Spatially Curved Thin-Walled Beams
|
Multiplying (3.21) by kikj and considering (3.15)–(3.17) and (3.46) yields |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dxðkÞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
G 1E |
|
|
|
|
|
|
|
|
|
|
|
E |
|
|
E |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
rij;ðkþ1Þ kikj ¼ |
xðkþ1Þ þ |
|
|
gðkÞ |
|
cos |
u hðkÞ |
sin |
u |
: |
|
ð |
3:47 |
Þ |
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
ds |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
Multiplying (3.21) successively by kikj and kisj and considering (3.15)–(3.17), |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
we obtain |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
G 1 |
|
|
|
|
|
|
|
|
|
|
|
|
dhðkÞ |
|
|
oxðkÞ |
|
|
|
|
K |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
¼ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
þ lð |
þ sÞgðkÞ |
|
|
|
|
|
sin |
u |
; |
|
||||||||||||||||||||||||||||||||
|
rij;ðkþ1Þ ki j |
|
|
|
lhðkþ1Þ þ l ds |
|
|
þ l ox |
|
|
|
|
l xðkÞ |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ð3:48Þ |
||||
|
s |
|
|
|
G 1 |
|
|
|
|
|
|
|
|
|
|
|
|
dgðkÞ |
|
|
oxðkÞ |
|
|
|
|
K |
|
|
|
|
|
|
|
|
|
|
cos |
|
: |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lð |
þ sÞhðkÞ |
þ l |
xðkÞ |
u |
|
||||||||||||||||||||||||||||||||||
rij;ðkþ1Þ ki j |
¼ |
|
|
lgðkþ1Þ þ l ds |
|
|
þ l oy |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ð3:49Þ |
||||
|
Multiplying (3.23) successively by ki; ki; and si and considering (3.15)–(3.17), |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
we find |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
qxðkþ1Þ ¼ |
G 1 |
½rij;ðkþ1Þ&kikj |
þ |
dð½rij;ðkÞ&kikjÞ |
þ |
oð½rij;ðkÞ&kikjÞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
ds |
|
|
|
|
|
|
|
|
ox |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
oð½rij;ðkÞ&kisjÞ |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
s |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
þ |
þ |
|
|
|
½rij;ðkÞ&ki |
sin |
|
|
|
|
|
|
|
|
|
cos |
u |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
oy |
|
|
|
|
|
|
j |
|
|
|
|
u ½rij;ðkÞ&ki j |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dxðkÞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
G 1 G 1 |
|
|
|
|
|
|
|
2 |
|
2 |
|
|
|
|
|
sin |
|
|
|
|
|
cos |
|
|
|
|
|
0 |
|
|
|
|
|
||||||||||||||||||||||
|
þ |
xðkþ1Þ |
|
hðkÞ |
|
u |
gðkÞ |
u |
|
|
|
|
rkk |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ds |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
þ fiðk 1Þkirkk0 ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ð3:50Þ |
||||||||||||||
|
G 1 |
½rij;ðkþ1Þ&ki |
k |
j þ |
dð½rij;ðkÞ&kikjÞ |
þ ð |
K |
|
|
|
|
|
|
|
s |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
qhðkþ1Þ ¼ |
|
|
|
|
|
|
|
|
|
|
ds |
|
|
|
|
|
|
|
þ sÞ½rij;ðkÞ&ki |
j |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dhðkÞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
||||||||||
|
þ G |
|
|
|
G |
|
hðkþ1Þ |
2 |
|
|
|
|
|
|
|
2 |
gðkÞðK |
þ sÞ xðkÞ sin u |
|
rkk |
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
ds |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
½rij;ðkÞ&kikj sin u þ fiðk 1Þkirkk0 ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ð3:51Þ |
|||||||||||||||||||||||||||||||||
|
G 1 |
|
|
|
|
|
|
|
|
|
s |
|
|
dð½rij;ðkÞ&kisjÞ |
|
ð |
K |
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
qgðkþ1Þ ¼ |
|
|
½rij;ðkþ1Þ&ki j þ |
|
|
|
|
|
|
|
ds |
|
|
|
|
|
|
|
þ sÞ½rij;ðkÞ&ki j |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
dgðkÞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|||||||||||
|
þ G |
|
|
|
G |
|
gðkþ1Þ |
2 |
|
|
þ 2 hðkÞðK þ sÞ xðkÞ cos u |
|
|
|
rkk |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
ds |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
þ ½rij;ðkÞ&kikj cos u þ fiðk 1Þsirkk0 |
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ð3:52Þ |
|||||||||||||||||||||||||||||||||
where functions fiðk 1Þ are presented in Appendix 2.

3.1 Theory of Thin-Walled Beams Based on 3D Equations
Considering (3.48), (3.49) and (3.28)–(3.30), we have
oð½rij;ðkÞ&kikjÞ |
|
|
K |
1k |
e1y |
|
|
ox |
¼ lð |
|
þ sÞxðk 1Þ |
l xðk 1Þ sin u; |
|||
oð½rij;ðkÞ&kisjÞ |
¼ lð |
K |
1k |
e1x |
cos |
u: |
|
oy |
|
|
þ sÞxðk 1Þ |
þ l xðk 1Þ |
|
||
29
ð3:53Þ
ð3:54Þ
Substituting (3.28)–(3.30) in (3.47)–(3.49) and integrating the final equations over the cross-sectional area of the beam, we obtain
Z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx0 |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
1 |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ðkÞ |
|
|
|
|
|
|
|
|
||||
Nkðkþ1Þ ¼ ½rij;ðkþ1Þ&kikjdF ¼ G |
EFxðkþ1Þ |
þ EF |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
ds |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
F |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
EF gð0kÞ cos u hð0kÞ sin u |
þ EF ax cos u þ ay sin u xð1kkÞ; |
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ð3:55Þ |
||
|
Z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dhð0kÞ |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
1 |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
||||
Qkxðkþ1Þ ¼ ½rij;ðkþ1Þ&kikjdF ¼ G |
|
lFhðkþ1Þ |
þ lF |
|
|
|
|
|
|
|
|||||||||||||||||
|
ds |
|
|
|
|
||||||||||||||||||||||
|
F |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
þ lFxeð1kyÞ þ lFðK þ sÞgð0kÞ lF xð0kÞ sin u |
|
|
|
|
||||||||||||||||||||||
|
|
G 1 |
|
F 1k |
|
|
|
|
dx1k |
|
|
|
|
|
|
|
|
|
|
1k a |
|
|
3:56 |
|
|||
|
|
l |
a |
y þ l |
F |
|
ðkÞa |
y l |
F |
ð |
K |
|
|
|
|
; |
ð |
Þ |
|||||||||
|
|
xðkþ1Þ |
|
|
ds |
|
|
|
|
þ sÞxðkÞ x |
|
|
|||||||||||||||
|
Z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dg0 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
1 |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ðkÞ |
|
|
|
|
|||||
Qkyðkþ1Þ ¼ ½rij;ðkþ1Þ&kisjdF ¼ G |
|
lFgðkþ1Þ |
þ lF |
|
|
|
|
|
|
|
|||||||||||||||||
|
|
ds |
|
|
|
|
|||||||||||||||||||||
|
F |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e1x |
|
|
|
|
0 |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|||
|
þ lFxðkÞ lFðK þ sÞhðkÞ |
|
þ lF xðkÞ cos u |
|
|
|
|
||||||||||||||||||||
|
|
1 |
|
1k |
|
|
|
|
dx1k |
|
|
|
|
|
|
|
|
|
|
1k |
|
|
|
|
|||
|
|
|
|
|
|
|
|
ðkÞ |
|
|
|
|
|
|
|
|
|
|
|
ð3:57Þ |
|||||||
|
þ G |
lFxðkþ1Þax lF |
ds |
ax lFðK þ sÞxðkÞay |
: |
||||||||||||||||||||||
Substituting (3.28)–(3.30) in (3.50)–(3.52) and then integrating over the crosssectional area, we find
|
F |
0 |
|
G 1N |
|
|
dNkðkÞ |
|
|
2 Q |
|
sin |
|
|
2 Q |
|
cos |
|
|
|
|
|||||
q |
xðkþ1Þ |
¼ |
|
|
þ |
kxðkÞ |
u |
kyðkÞ |
u |
|
|
|
||||||||||||||
|
|
kðkþ1Þ þ |
|
|
ds |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
1 |
( |
|
0 |
|
|
|
dx0 |
|
|
|
0 |
|
|
0 |
|
) |
0 |
|
||||
|
|
|
|
1 |
|
|
|
|
|
ðkÞ |
|
|
|
|
|
|
|
|||||||||
|
|
|
þ G |
F G |
xðkþ1Þ |
2 |
|
|
|
2 hðkÞ |
sin u gðkÞ cos u |
rkk |
|
|||||||||||||
|
|
|
|
ds |
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
e1y |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
e1x |
|
|
|
|
|
|
|
|
|
|
|
|
|
1k |
|
|
|
||||
|
|
|
þ lF xðk 1Þ cos u xðk 1Þ sin u |
|
þ 2lFðK þ sÞxðk 1Þ |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
Ff 0 |
|
0 ; |
|
|
3:58 |
|
|
|
|
|
|
2G 1F a sin |
u |
þ |
cos |
|
1k |
0 |
þ |
|
|
ð |
Þ |
|||||||||||
|
|
|
|
y |
|
|
x |
|
u xðkÞrkk |
iðk 1Þkirkk |
|
|
||||||||||||||

30 3 Transient Dynamics of Pre-Stressed Spatially Curved Thin-Walled Beams
|
F |
0 |
|
|
G 1Q |
|
|
|
|
|
|
|
|
dQkxðkÞ |
|
|
K |
|
|
|
|
Q |
|
|
|
|
N |
|
|
|
|
sin |
|
|
|
|
|
|
||||||||||||||||
q |
hðkþ1Þ |
¼ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
kyðkÞ |
kðkÞ |
u |
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
kxðkþ1Þ þ |
ds |
þð þsÞ |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
( |
|
|
|
|
1 |
0 |
|
|
|
dhð0kÞ |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
) |
0 |
|
|
|||||||||
|
|
|
þG |
|
F |
|
|
G |
hðkþ1Þ 2 |
|
|
2 |
gðkÞðK þsÞ xðkÞ |
sinu |
rkk |
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
ds |
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx1k |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
F |
|
|
1k |
|
|
a |
|
|
G 2F |
|
1k |
|
a |
|
0 |
|
|
2G 1F |
|
|
ðkÞ |
a |
0 |
|
|
|
|
|||||||||||||||||||||
|
|
|
q |
|
|
|
|
y þ |
|
|
yrkk |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
xðkþ1Þ |
|
|
|
|
|
xðkþ1Þ |
|
|
|
|
|
|
|
ds |
|
|
yrkk |
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
þ |
2G 1Fa |
xð |
K |
|
|
|
1k 0 |
þ |
Ff |
0 |
|
|
k |
|
0 |
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
ð |
3:59 |
Þ |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
þsÞxðkÞrkk |
|
iðk 1Þ |
|
irkk |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
0 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
dQkyðkÞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
qFgðkþ1Þ |
¼ G |
|
Qkyðkþ1Þ þ |
|
|
|
ðK þ sÞQkxðkÞ þ NkðkÞ cos u |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
ds |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
( |
|
|
1 |
0 |
|
|
|
|
|
dg0 |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
) |
0 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ðkÞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
þ G |
|
F |
|
|
G |
gðkþ1Þ 2 |
|
þ |
2 |
|
hðkÞðK |
þ sÞ xðkÞ |
cos u rkk |
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
ds |
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx1k |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
F |
|
|
|
1k |
|
|
a |
|
|
G 2F |
|
|
1k |
|
|
a |
|
|
0 |
|
|
2G 1F |
|
|
|
ðkÞ |
a |
|
0 |
|
|
|
|||||||||||||
|
|
|
þ q |
|
|
|
|
|
|
|
|
|
|
xrkk |
þ |
|
|
|
xrkk |
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
xðkþ1Þ |
x |
|
|
|
xðkþ1Þ |
|
|
|
|
|
|
|
|
ds |
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
þ |
2G 1Fa |
|
K |
|
|
|
1k 0 |
þ |
Ff 0 |
|
|
s |
0 |
|
: |
|
|
|
|
|
|
|
|
|
|
ð |
3:60 |
Þ |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
yð þ sÞxðkÞrkk |
|
|
iðk 1Þ |
|
irkk |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
Substituting (3.55)–(3.57) in (3.58)–(3.60) with due account for (3.37)–(3.39) yields
2 |
2 |
2 |
0 |
0 |
|
|
1 |
|
2 |
0 |
dx0 |
|
|
|
||
|
|
|
|
ðkÞ |
|
|
|
|||||||||
G |
ðqG |
qG1 |
rkk |
Þxðkþ1Þ |
¼ 2G |
|
|
qG1 |
þrkk |
|
|
|
|
|
|
|
|
|
|
ds |
|
|
|
||||||||||
|
|
|
|
|
G 1 |
|
|
|
|
|
þ2rkk0 |
|
h |
|
||
|
|
|
|
|
qG12 þ2qG22 |
|
ax cosuþay sinu xð1kkÞ |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
ð3:61Þ |
|
|
|
|
|
|
gð0kÞ cosuþhð0kÞ sinu þF1ðk 1Þ; |
|||||||||||
G 2ðqG2 qG22 r0kkÞðh0ðkþ1Þ þ ayx1ðkkþ1ÞÞ
¼2G 1ðqG22 þ r0kkÞ
dds h0ðkÞ þ ayx1ðkkÞ þ ðK þ sÞ g0ðkÞ axx1ðkkÞ
þ G 1 qG12 þ qG22 þ 2rkk0 xð0kÞ sin u |
|
|
n |
o |
ð3:62Þ |
þ G 1qG22 xð1kyÞ xð0kÞ sin / þ gð0kÞðK þ sÞ |
þ F2ðk 1Þ; |

3.1 Theory of Thin-Walled Beams Based on 3D Equations |
|
31 |
|||||
G 2ðqG2 qG22 rkk0 Þðgð0kþ1Þ axxð1kkþ1ÞÞ |
|
|
|||||
|
|
d |
|
|
|
|
|
¼ 2G 1 |
qG22 þ rkk0 |
|
|
|
gð0kÞ axxð1kkÞ ðK þ sÞ hð0kÞ þ ayxð1kkÞ |
|
|
|
ds |
|
|
||||
G 1 qG21 þ qG22 þ 2r0kk x0ðkÞ cos u
|
|
|
|
n |
|
|
|
|
|
|
o |
|
|
|
|
|
|
þ |
G 1 |
q |
G2 |
|
1x |
0 |
cos |
0 |
ð |
K |
þ sÞ þ |
F |
3ðk 1Þ |
; |
ð |
3:63 |
Þ |
|
2 |
xðkÞ |
þ xðkÞ |
|
/ hðkÞ |
|
|
|
|
||||||||
where G12 ¼ Eq 1; |
G22 ¼ lq 1; and functions Fjðk 1Þ ðj ¼ 1; 2; 3Þ are presented in |
||||||||||||||||
Appendix 2.
Let us substitute formulas (3.28)–(3.30) in (3.47)–(3.49), then multiply (3.47) successively by x, y, and xA; and (3.48) by ðy ayÞ and (3.49) by ðx axÞ; and integrate the obtained equations over the cross-sectional area of the beam. As a
result we obtain
Z
|
|
M |
xðkþ1Þ |
¼ ½rij;ðkþ1Þ&kikj |
ydF |
¼ |
G 1 |
q |
G2I |
e1x |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
1 |
x xðkþ1Þ |
|
|
|
|||||||||||||||
|
|
|
|
F |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
e1x |
|
|
|
|
|
2 1k |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
dxðkÞ |
|
|
|
|
|
|
|
|
|
|
|
|
ð3:64Þ |
||||||||
|
|
|
|
þ qG1Ix |
|
|
|
IxqG1xðkÞ |
sin u; |
|
|
|
|
|||||||||||||
|
|
|
|
|
ds |
|
|
|
|
|||||||||||||||||
|
|
|
|
Z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M |
yðkþ1Þ |
¼ ½rij;ðkþ1Þ&kikj |
xdF |
¼ |
G 1 |
q |
G2I |
e1y |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
1 |
y xðkþ1Þ |
|
|
|
|||||||||||||||
|
|
|
|
F |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
e1y |
|
|
|
|
2 |
|
1k |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
dxðkÞ |
|
|
|
|
|
|
|
|
|
|
|
|
ð3:65Þ |
||||||||
|
|
|
|
þ qG1Iy |
|
|
|
qG1IyxðkÞ |
cos u; |
|
|
|
|
|||||||||||||
|
|
|
|
|
ds |
|
|
|
|
|||||||||||||||||
|
|
Z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e |
|
|
|
|
B |
|
|
|
|
dF |
|
|
G 1 |
|
|
G2I |
e |
|
|
|
G2I |
|
dwðkÞ |
; |
|
3:66 |
|
||||
ðkþ1Þ |
¼ ½rij;ðkþ1Þ&kikjxA |
¼ |
q |
x wðkþ1Þ þ q |
|
ð |
Þ |
|||||||||||||||||||
|
|
|
|
|
|
1 |
1 |
x ds |
|
|||||||||||||||||
|
|
F |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z |
|
|
|
|
|
|
|
Z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
MAðkþ1Þ ¼ |
½rij;ðkþ1Þ&kisjðx axÞdF ½rij;ðkþ1Þ&kikjðy ayÞdF |
|
|
|
||||||||||||||||||||||
|
|
F |
|
|
|
|
|
|
|
F |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z |
|
|
|
Z |
|
|
|
|
|
|
|
|
|
|
Z |
|
|
|
|
|
|
|
||
|
¼ |
½rij;ðkþ1Þ&kisjxdF |
|
|
½rij;ðkþ1Þ&kikjydF ax |
|
½rij;ðkþ1Þ&kisjdF |
|
|
|
||||||||||||||||
|
|
F |
|
|
|
F |
|
|
|
|
|
|
|
|
|
|
F |
|
|
|
|
|
|
|
||
|
|
Z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
þ ay |
½rij;ðkþ1Þ&kikjdF ¼ MCðkþ1Þ axQkyðkþ1Þ þ ayQkxðkþ1Þ |
|
|
|
||||||||||||||||||||
|
|
F |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 A 1k |
|
|
|
|
dx1k |
|
|
|
2 |
|
0 |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
2 A |
|
ðkÞ |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
¼ G |
qG2Ip xðkþ1Þ þ qG2Ip |
|
|
|
qG2F xðkÞ |
ax cos u þ ay sin u |
|
||||||||||||||||||
|
|
ds |
|
|
||||||||||||||||||||||
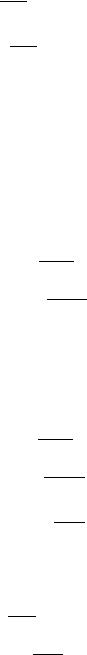
32 |
|
|
|
3 |
Transient Dynamics of Pre-Stressed Spatially Curved Thin-Walled Beams |
||||||||||||
|
|
|
|
|
( |
|
|
|
|
dg0 |
|
|
|
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
a |
F |
|
G2 |
G 1 |
0 |
|
|
ðkÞ |
|
|
K |
|
0 |
|
||
þ |
q |
gðkþ1Þ |
|
þ ð |
þ sÞhðkÞ |
|
|||||||||||
x |
|
2 |
|
|
|
ds |
|
|
|||||||||
|
|
|
|
|
( |
|
|
|
|
|
dhð0kÞ |
|
|
|
) |
|
|
|
a F |
|
G2 |
|
G 1 |
0 |
|
|
|
|
K |
0 |
|
||||
|
q |
|
hðkþ1Þ |
|
|
|
|
þ sÞgðkÞ |
|
||||||||
þ |
|
þ ds |
þ ð |
|
|||||||||||||
y |
|
2 |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
þ qG22 xeð1kyÞIy cos u þ xeð1kxÞIx sin u |
þ qG22F ay xeð1kyÞ ax xeð1kxÞ |
; ð3:67Þ |
|||||||||||||||
and Myðkþ1Þ are the discontinuities in the derivatives of the bending moments with respect to the x- and y-axes, Bðkþ1Þ are the discontinuities in the derivatives of the bimoment, MAðkþ1Þ are the discontinuities in the derivatives of the bending-torsional moment, and IpA ¼ Ix þ Iy þ ða2x þ a2y ÞF:
Now we substitute formulas (3.28)–(3.30) in (3.50)–(3.52), then multiply (3.50) by x, y, and xA; while (3.51) and (3.52) by ðy ayÞ and ðx axÞ; respectively, and integrate the obtained equations over the cross section of the beam. As a result, we obtain
e1y |
¼ |
G 1I 1M |
|
|
|
|
|
I 1 |
dMyðkÞ |
þ |
2 sin |
ulð |
K |
1k |
|
|
|
|||||||||||||||||||
qxðkþ1Þ |
|
|
y |
|
yðkþ1Þ þ |
y |
|
|
ds |
|
|
|
|
|
|
|
þ sÞxðk 1Þ |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx1k |
! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
þ |
2 cos |
ul |
|
G 1 |
1k |
|
|
|
|
ðk 1Þ |
|
|
2 2 |
e1y |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
ds |
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
xðkÞ |
|
|
|
|
|
|
|
lxðk 1Þ |
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1y |
|
|
|
|
|
|
|
|
|
|
|
! |
|
|
|
||
|
|
|
0 |
|
2 e |
1y |
|
|
|
|
|
|
|
|
|
e |
|
|
|
|
|
1 |
|
|
|
|
|
1k |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
1 dxðkÞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
þ rkk |
G |
xðkþ1Þ |
|
2G |
|
|
|
|
|
|
þ |
2G |
cos uxðkÞ |
|
|
|
|
||||||||||||||||||
|
|
|
|
ds |
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
Z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
þ Iy 1rkk0 |
F |
fiðk 1ÞkixdF; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ð3:68Þ |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e1x |
¼ |
G 1I 1M |
|
|
|
|
|
I 1 |
dMxðkÞ |
|
|
2 cos |
ulð |
K |
1k |
|
|
|
||||||||||||||||||
qxðkþ1Þ |
|
|
x |
|
xðkþ1Þ þ |
x |
|
|
ds |
|
|
|
|
|
|
|
þ sÞxðk 1Þ |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx1k |
! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
þ |
2 sin |
ul |
|
G 1 |
|
1k |
|
|
|
ðk 1Þ |
|
|
2 2 |
|
e1x |
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
xðkÞ |
|
|
ds |
|
|
|
|
|
|
lxðk 1Þ |
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1x |
|
|
|
|
|
|
|
|
|
|
|
! |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
0 |
G 2 e |
1x |
|
|
|
2G 1 |
dxðkÞ |
|
|
2G 1 |
sin |
1k |
|
|
|
|
|||||||||||||||||
|
þ rkk |
|
|
|
|
|
þ |
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
ds |
|
|
|
|
||||||||||||||||||||||||||
|
|
xðkþ1Þ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
uxðkÞ |
|
|
|
|
||||||||||||
|
|
|
|
|
Z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
þ Ix 1rkk0 |
F |
fiðk 1ÞkiydF; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ð3:69Þ |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e |
G 1I |
1B |
ðkþ1Þ |
þ |
I 1 |
dBðkÞ |
|
2 2 e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
qwðkþ1Þ ¼ |
|
x |
x |
|
|
ds |
|
|
|
lwðk 1Þ |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
G 2 e |
|
|
|
2G 1 |
dwðkÞ |
|
|
|
I 1 |
|
|
0 |
|
|
|
f |
|
|
|
dF; |
|
3:70 |
|
||||||||||
þ rkk |
|
|
|
|
þ |
rkk |
|
|
|
iðk 1ÞkixA |
ð |
Þ |
||||||||||||||||||||||||
|
|
wðkþ1Þ |
|
|
|
|
|
ds |
x |
|
|
|
|
|
|
|
||||||||||||||||||||
F
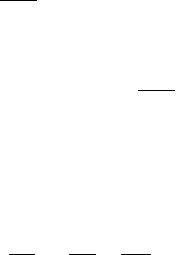
3.1 Theory of Thin-Walled Beams Based on 3D Equations |
|
|
|
33 |
|||||||||||||||||||||||||||||||
qxð1kkþ1ÞIpA qgð0kþ1ÞaxF þqhð0kþ1ÞayF |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
¼ |
G 1M |
|
|
|
|
|
dMAðkÞ |
|
þ |
cos |
u |
M |
yðkÞ þ |
sin |
u |
M |
|
|
|
|
|||||||||||||||
|
|
|
Aðkþ1Þ þ |
ds |
|
|
|
|
|
|
|
|
|
|
|
|
xðkÞ |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
G 1F axhð0kÞ þaygð0kÞ |
|
|
||||||
ax cosuþay sinu NkðkÞ ðK þsÞl |
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
dhð0k 1Þ |
! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
! |
|
|
|
||||
|
|
|
|
e1y |
|
|
|
|
|
|
|
|
|
|
|
|
e |
1x |
|
|
dgð0k 1Þ |
|
|
|
|
||||||||||
axF xðk 1Þ |
þ |
|
|
|
|
|
ayF xðk 1Þ þ |
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
ds |
|
|
ds |
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
þðK þsÞ axFgð0k 1Þ þayFhð0k 1Þ þIpAxð1kk 1Þ |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
) |
|||
þ sinu axFxð0k 1Þ Iy xeð1ky 1Þ |
|
þ cosu ayFxð0k 1Þ þIx xeð1kx 1Þ |
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
þrkk0 G 2 axFgð0kþ1Þ þayFhð0kþ1Þ þIpAxð1kkþ1Þ |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
( |
|
|
|
|
|
dg0 |
|
|
|
|
|
|
dh0 |
|
|
|
|
|
dx1k |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
2 |
0 G 1 |
|
a |
|
F |
ðkÞ |
|
|
a |
F |
|
|
ðkÞ |
|
|
IA |
|
|
ðkÞ |
|
|
|
K |
|
F a 0 |
a |
0 |
|||||||
|
|
|
þ |
|
|
|
|
|
|
þð |
þsÞ |
ygðkÞ |
|||||||||||||||||||||||
|
|
rkk |
|
|
x |
|
|
ds |
y |
|
|
|
|
ds |
þ p |
|
|
ds |
|
xhðkÞ |
þ |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
) |
|
|
||||
þ cosu axFxð0kÞ þIy xeð1kyÞ þ sinu ayFxð0kÞ þIx xeð1kxÞ |
|
|
|||||||||||||||||||||||||||||||||
|
|
|
Z |
|
fiðk 1Þsiðx axÞ fiðk 1Þkiðy ayÞ dF: |
|
|
|
|
|
|
ð3:71Þ |
|||||||||||||||||||||||
þrkk0 |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
F |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Substituting (3.64)–(3.67) and (3.37)–(3.39) in (3.68)–(3.71) yields |
|||||||||||||||||||||||||||||||||||
G 2ðqG2 qG12 rkk0 |
h |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
||||||||||||||
Þ xð1kxþ1Þ þ xð0kþ1Þ cos u hð0kþ1ÞðK þ sÞ |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
d h |
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
||||||||
|
|
|
|
¼ 2G 1 |
|
|
qG12 þ rkk0 |
|
|
|
|
xð1kxÞ þ xð0kÞ cos u hð0kÞðK þ sÞ |
|
||||||||||||||||||||||
|
|
|
|
|
|
|
ds |
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
þ 2rkk0 |
|
|
|
|
|
|
|
|
|
|
|
ð3:72Þ |
||||||
|
|
|
|
|
þ qG12 þ 2qG22 |
|
G 1xð1kkÞ sin u þ F4ðk 1Þ; |
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
h |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
G 2ðqG2 qG12 rkk0 Þ xð1kyþ1Þ xð0kþ1Þ sin u þ gð0kþ1ÞðK þ sÞ |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
d h |
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|||||||
|
|
|
|
¼ 2G 1 |
|
|
qG12 þ rkk0 |
|
|
|
xð1kyÞ xð0kÞ sin u þ gð0kÞðK þ sÞ |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
ds |
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ð3:73Þ |
|
|
|
|
|
þ qG12 þ 2qG22 |
|
þ 2rkk0 G 1xð1kkÞ cos u þ F5ðk 1Þ; |
|
|||||||||||||||||||||||||||
