
Учебное пособие 1295
.pdfдостигается путем инверсии программы-потребителя, что обеспечивает выполнение ее функции с помощью обращения к отдельным секциям инвертированной программы из програм- мы-поставщика.
3.4. Методы построения алгоритмов
При разработке алгоритмов следует пользоваться стандартными подходами. Если метод решения сначала не очевиден, то проблему следует проанализировать, чтобы точно определить исходные условия и цели. Может оказаться, что проблема станет разрешимой или частично разрешимой, если будет использована некоторая дополнительная информация. Иногда проблему можно разбить на части, которые проще поддаются решению. При определенных обстоятельствах может быть использован такой подход: сначала находится приближенное решение, которое затем уточняется.
Способ пошагового уточнения и другие методы декомпозиции программ определяют основу для построения программных модулей. Они обеспечивают методологию проектирования и удобные способы ведения записи в процессе разработки программ путем ее разбиения на отдельные модули [5]. Но эти методы оказываются менее пригодными при проектировании тех модулей, которые предназначены для преобразования данных.
3.4.1. Метод «разделяй и властвуй»
Некоторые проблемы по природе носят аддитивный характер. Такие проблемы можно разделить на части, и решение всей проблемы можно получить с помощью решения ее частей. При таком подходе можно использовать параллельную обработку. Задание начальных значений элементов массива осуществляется для всего массива и выполняется с помощью тех же
71

начальных значений для частей массива. Матричные операции сложения и вычитания выполняются таким же способом, так как эти операции определены для отдельных элементов. На том же принципе строится и численное интегрирование. Аналогичным примером из экономики служит двойной бухгалтерский учет, когда итоги по столбцам вычисляются для различных категорий, включающих дебиты и кредиты, после чего результаты в нужных сочетаниях сравниваются.
Простым примером использования аддитивности служит задача вычисления площади неправильного многоугольника с помощью разбиения его на треугольники и вычисления их площадей по отдельности (рис.3.1). Площадь всего многоугольника равна сумме площадей его частей.
A B
E D C
D C 
Рис. 3.1. Площадь неправильного прямоугольника: S=A+B+C+D+E.
В сортировке слиянием, выполняющейся разделением n элементов списка на две группы и с помощью сортировки каждой из них с последующим их слиянием, используется подход «разделяй и властвуй».
Сортировка Шелла также основана, на использовании принципа «разделяй и властвуй». Сначала список разбивается на n/2 подсписков, содержащих по два элемента каждый. Подсписки сортируются. На втором внешнем цикле сортировка производится над n/4 четырехэлементными, затем над n/8 восьмиэлементными списками. На первый взгляд не очевидно, что на каждом цикле сортируется различное число подсписков, так как подсписки перемешиваются друг с другом:
72
procedure сортировка Шелла (список); число групп = n/2;
while (число групп 1) do i:=1;
j:=1+ число групп; while j n do
if список (i) > список (j) обменять(список(i),список(j)); i:=i+1;
j:=j+1;
число групп:= число групп/2 end.
Во многих ЭВМ деление чисел на части выполняется на аппаратном или на микропрограммном уровне. Вычисления могут производиться каждый раз над одним байтом, при этом используется прямой и обратный переносы между соседними парами байтов. Это тоже иллюстрирует принцип «разделяй и властвуй».
Алгоритм двоичного поиска, однако, не является аддитивным, хотя в нем и используется разделение списка на части. Каждый раз берется одна из двух частей. Но при решении задачи поиска вершины в неупорядоченном дереве может быть использован алгоритм типа «разделяй и властвуй». Дерево разделяется на поддеревья, и поиск осуществляется по всем поддеревьям. Каждое из поддеревьев может быть в свою очередь также разделено на части. Получаем, таким образом, рекурсивную процедуру. Если дерево — двоичное, поиск по нему производится с помощью следующей процедуры:
procedure поиск (дерево); if дерево = nil
return (неудача)
else if дерево_вершина=вершина_требуемая return (удача)
73
else
искать (левое-поддерево); if удача
return (удача) else
искать (правое_поддерево); if удача
return (удача)
else return (неудача) end.
Поиск в левом поддереве и поиск в правом имеют одинаковый приоритет. При параллельной обработке они могут быть исследованы одновременно.
3.4.2. Метод последовательных приближений
Когда известно приближенное решение и есть способы для его уточнения, можно использовать подход, описанный ниже. Начиная с исходного приближения f0 производится последовательное уточнение решения f1, затем уточнение решений f2, f3 и т. д. Этот ряд представляет собой последовательность приближенных решений, которые или сходятся к действительному решению, или приближаются к нему настолько, насколько это нужно для практического использования. Каждый член последовательности может зависеть или только от предшествующего ему члена, или от всех более ранних приближений [2].
Метод Ньютона-Рафсона для вычисления квадратного корня представляет собой пример такого подхода. Последовательные приближения используются также для математических функций, обычно представляемых такими рядами, как
sin(x) x |
x3 |
x5 |
x7 |
|
||||
|
|
|
|
|
... |
(3) |
||
3! |
5! |
7! |
||||||
|
|
|
|
|
||||
74
Частичные суммы представляют собой сходящийся ряд приближений функции синуса. Они могут быть вычислены рекурсивно; при этом члены ряда задаются также с помощью рекурсивного соотношения:
|
|
|
|
для k 0, |
|||
|
|
tk |
|||||
sink (x) |
|
|
|
|
|||
|
|
|
|
|
|
для k 0, |
|
|
|
sink 1(x) tk |
|||||
|
|
для |
|
k 0, |
(4) |
||
|
|
|
|||||
x |
|
|
|||||
|
|
|
|
|
|
|
|
tk |
|
x |
2 |
tk 1 |
|
|
|
|
|
|
|
для |
k 0. |
||
|
|
|
|
|
|||
|
2k(2k 1) |
|
|||||
|
|
||||||
Каждый из членов зависит только от предшествующего, каждое новое приближение к функции синуса соответственно зависит от ранее полученного приближения и нового члена ряда. Итерационная реализация более эффективна, чем рекурсивная, так как при использовании рекурсии приходится выполнять избыточные вычисления членов ряда. К сожалению, эти ряды при больших значениях х сходятся слишком медленно, и поэтому их нельзя использовать в пакетах подпрограмм для вычисления функции синуса.
Другим примером сходящихся приближений служит численное интегрирование. Определенный интеграл представляет собой площадь между кривой, изображающей функцию, и осью абсцисс. Для вычисления интеграла отрезок, на котором он определен, делится на равные части, и на каждой из этих частей вычисляется приближение с помощью значения f(xk) x, где xk - некоторое значение x в пределах k-й части, а x - размер каждой из частей отрезка. Затем производится дальнейшее разбиение частей на более мелкие, и вычисляется следующее приближение. Когда два приближения достаточно близки друг к другу, то решение найдено. В этом примере использовались два различных способа построения алгоритма: аддитивный ме-
75
тод применялся для нахождения последовательных приближений к значению интеграла.
Метод последовательных приближений можно использовать, если известно, что существует такая формула, которая обеспечивает сходимость к желаемой величине. Затем, когда два приближенных ответа имеют достаточно близкие значения, они принимаются примерно одинаково близкими к действительному решению. Этот метод при численных расчетах следует использовать очень осторожно, так как влияние погрешностей вычислений на ЭВМ возрастает со временем.
3.4.3. Метод наискорейшего спуска
Название этого метода отражает заложенный в него принцип: для того чтобы достигнуть дна, требуется лишь идти вниз. Следует отметить, что движение вниз не гарантирует достижения самой низкой точки. Вместо этого отыскивается дно первого обнаруженного углубления. В начале поиска необходимо очень аккуратно выбирать исходную точку. Рассматриваемый метод позволяет получить хороший результат при решении задачи, когда нельзя найти оптимальное решение, потому что получение наилучшего решения или невозможно, или обходится слишком дорого.
Метод наискорейшего спуска отличается от метода последовательных приближений тем, что во втором случае за исходное берется любое приближение, которое затем улучшается. В рассматриваемом же методе направление каждого шага планируется так, чтобы он был направлен в сторону нужного решения. Использование метода последовательных приближений при создании программ заключается в том, что, принимая ка- кую-либо работающую программу за исходную, производится ее последовательное улучшение с помощью отладки и настройки. Способ наискорейшего спуска применяется в методах нисходящего проектирования и частично в методе пошагового уточнения.
76
Задача коммивояжера представляет собой классический пример задачи, которую легко поставить, но очень трудно решить. Коммивояжер должен посетить некоторое множество городов, и задача заключается в том, чтобы найти кратчайший маршрут, следуя которому он может попасть во все города не более одного раза и вернуться в исходную точку. Во все города можно попасть из любого другого или по прямому пути между ними, или через другие города. На рис. 3.2 показана постановка одной такой задачи. Города обозначены буквами. Город А является исходным пунктом маршрута. Цифрами указаны относительные расстояния между городами. Решение данной задачи выполняется с помощью недетерминированного алгоритма. Один из возможных способов получения решения заключается в генерации всех перестановок городов, когда А — исходный путь маршрута. Пря этом возможны такие комбинации, в которых рядом будут расположены города, не имеющие прямых путей между ними. Устранив эти комбинации, с помощью вычисления длины маршрутов среди оставшихся можно определить кратчайший из них.
Хорошее, но не обязательно оптимальное решение может быть найдено с помощью метода наискорейшего спуска. Начиная с города А, следующим для посещения выбирается ближайший другой город. От этого города берется следующий участок маршрута, представляемый кратчайшим расстоянием между этим городом и еще не посещенными городами. Этот процесс продолжается, пока не будут пройдены все города. Данный алгоритм имеет полиномиальную сложность. С помощью описанного метода после нахождения частичного пути А-В-Е (рис. 3.2) следует сделать выбор между Е-С и Е-D.
77
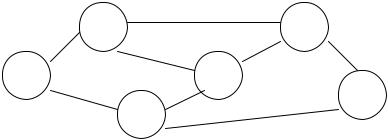
|
B |
4 |
C |
|
3 |
|
|||
2 |
1 |
1 |
||
|
A E
4 |
1 |
F |
D
5
Рис. 3.2. Граф 1 задачи о коммивояжере
Если выбран участок Е-С, получится маршрут А-В- Е-С- F-D-А, длина которого составляет 16. Этот путь представляет оптимальное решение для такого выбора. В том случае, когда выбран участок Е-D, маршрут найти нельзя, если только не устранить ограничение, по которому запрещается посещать один и тот же город дважды. На самом деле, если снять это ограничение, можно использовать более короткий путь, проходящий от F к D через С и Е. При этом общая длина маршрута будет равна 14.
3.4.4. Метод обратного прохода
Этим методом можно решить некоторые хорошо известные головоломки. Пусть имеются два резервуара; объем одного из них измеряется пятью, а объем другого — девятью чашками. Требуется с помощью этих резервуаров отмерить 6 чашек воды. Для решения задачи можно применить метод обратного прохода. Если можно было бы отмерить одну чашку воды, то, вылив ее в больший резервуар и добавив в него воду из другого резервуара объемом 5 чашек, можно было бы получить требуемый объем воды. Одна чашка воды может быть отмерена, если из полного меньшего резервуара отлить 4 чашки воды. Это можно сделать, если в большем резервуаре уже име-
78
ется 5 чашек воды. Таким образом, если наполнить меньший резервуар дважды и вылить эту воду в больший, в меньшем останется 1 чашка воды. Вода из большего резервуара выплескивается, и в него переливается оставшаяся 1 чашка из малого резервуара, из которого затем переливается еще 5 чашек воды. Таким образом найдена последовательность действий, соответствующая решению задачи, путем обратного прохода.
В другой задаче надо определить, сколько прыжков потребуется лягушке, чтобы выбраться из ямы глубиной 1 м, если за один прыжок лягушка поднимается на 30 см, а между прыжками сползает вниз на 20 см. Прослеживая путь лягушки в обратную сторону, находим, что она сможет выпрыгнуть из ямы, поднявшись на 70 см. Поскольку после каждого прыжка она поднимается на 10 см, ей потребуется 7 прыжков, чтобы подняться на 70 см. На восьмом прыжке лягушка выбирается наружу.
Метод обратного прохода применяется тогда, когда задан порядок (направление) решения некоторой задачи; замена этого направления на обратное может помочь упростить задачу без ее изменения. Этот метод можно использовать не всегда. Выдача последовательности чисел от 1 до 10 направлена, но необратима, так как перемена направления этой процедуры изменит результат. Задача нахождения всех простых чисел между 1 и 100 направлена и обратима, но, если начинать со старших чисел, решение ее существенно усложнится. Задача поиска пути в лабиринте направлена и обратима, если не осуществляется истинный поиск в «реальном» лабиринте. Однако, если за исходную точку взять выход и находить путь ко входу, такая задача аналогична первоначальной.
79

3.4.5. Метод динамического программирования
Метод динамического программирования заключается в одновременном использовании прямого и обратного проходов для решения задачи. Перемещение в одном направлении позволяет получить одно из возможных решений. Движение в другом направлении обеспечивает альтернативное решение. После сравнения этих решений выбирается лучшее из них. Классическим примером использования этого метода является решение варианта задачи о коммивояжере, в котором требуется найти кратчайшее расстояние между двумя пунктами. Эти пункты могут обозначать один и тот же город, при этом найденный путь представляет кратчайший циклический маршрут, следуя которому коммивояжер не повторяет ни один из участков пути.
4
2 7
5
1 9
3 8
6
Рис. 3.3. Граф 2 задачи о коммивояжере
На графе, приведенном на рис. 3.3, точками 1 и 9 отмечены соответственно исходный и конечный пункты маршрута. Допустим, что для каждого отрезка задана его длина. Применение обратного прохода для решения этой задачи заключается в том, что перед получением кратчайшего пути между точками 1 и 9 определяются кратчайшие пути от точки 2 к точке 9 и от точки 3 к точке 9. Для нахождения этих маршрутов необходимо определить кратчайшие пути из точек 4, 5 и 6 к точке 9.
Шаг 1. Анализ путей, ведущих к конечному пункту из соседних: 7-9, 8-9.
80
