
Учебное пособие 1295
.pdf
Когда s=S, то n=N, и приходим к выражению
|
|
S |
|
|
|
|
|
|
|
|
|
|
|
|
|||
conf ( N) |
s 1 |
, |
(24) |
||
|
|||||
N S 1N S
которое представляет степень уверенности в том, что все ошибки найдены. В таблице ниже приведены значения степеней уверенности, вычисленные по данным формулам, для разных значений намеренно внесенных и первоначально существующих ошибок.
Степень уверенности в обнаружении всех ошибок.
s=S |
n=N |
con f( N) |
5 |
0 |
0,83 |
10 |
0 |
0,91 |
20 |
0 |
0,95 |
5 |
1 |
0,71 |
10 |
1 |
0,83 |
20 |
1 |
0,91 |
5 |
2 |
0,625 |
10 |
2 |
0,77 |
20 |
2 |
0,87 |
Чем больше ошибок из числа намеренно внесенных было обнаружено, тем выше уверенность в надежности модуля. Но чем больше реально существующих ошибок обнаружено, тем вероятнее, что есть еще другие, которые пока обнаружить не удалось.
Уравнение
s |
N 1 conf ( N) |
, |
(25) |
|
|||
|
1 conf ( N) |
|
|
полученное из предыдущего уравнения, позволяет определить количество ошибок, которые должны быть намеренно внесены
161
в модуль, чтобы получить необходимую степень уверенности в его надежности. Причем считается, что тестирование продолжается до тех пор, пока все намеренно внесенные ошибки не будут обнаружены. Например, можно считать, что обнаружение 5 ошибок дает 90 % уверенности в том, что все ошибки найдены, если в модуль было намеренно внесено 60 ошибок и в процессе тестирования все были обнаружены.
Следует отметить, что необходимо вносить в модуль ошибки всех возможных типов, а именно: орфографические, пунктуационные, синтаксические, логические, ошибки в размещении, в типах данных и т.п. Можно ввести таблицу, в которой ошибки размещены в соответствии с их типами, и пользоваться ею. Можно случайно вносить ошибки в произвольным образом выбранные операторы модуля.
5.6.2. Ошибки объединения модулей
Фирмой IBM установлено, что в среднем одна ранее не обнаруженная ошибка появляется в каждых 100 операторах программы. Большинство ошибок содержится в сопряжениях модулей и операторах ввода-вывода. Такого рода ошибки затрагивают обычно сразу несколько модулей. После того как проведено тестирование отдельно каждого модуля, последние объединяются в систему. Экспериментально установлено, что в 90 % всех новых модулей и в 15 % старых необходимо вносить изменения. Приблизительно в 15 % новых модулей и 6 % старых следует внести более 10 % изменений. Если осталось D старых модулей и сформировано M новых, число необходимых изменений N определяется выражением
N=2*(0,9M+0,15D)+23*(0,15M+0,06D).
5.6.3. Другие оценки ошибок
Эксперименты показали, что число ошибок в неоттестированных программах пропорционально E2/3, где Е – мера Холстеда. Коэффициент пропорциональности равен примерно
162
1/3200. В программах, прошедших стадии тестирования и отладки, это отношение сохраняется, но коэффициент пропорциональности уменьшается.
Различные формулы оценки количества ошибок не учитывают вероятность внесения k новых ошибок при исправлении n старых.
Вероятность того, что новый тестовый прогон позволит обнаруживать ошибки, будет зависеть от процента оставшихся ошибок. Последние ошибки обнаружить труднее. Формула
|
1 |
n 1 |
1 |
|
|
|
avg(Tn ) |
|
, |
(26) |
|||
|
|
|||||
|
k 0 |
N k |
|
|||
позволяет установить среднее количество проверок, необходимых для обнаружения n ошибок. Здесь - неизвестное значение, которое может быть определено экспериментально.
Исходя из предыдущей формулы, получаем
|
|
|
n 1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
P |
avg(Tn ) |
|
N k |
|
|
|
|
|
k 0 |
|
, |
(27) |
|||
avg(TN ) |
N 1 |
1 |
|
||||
|
|
|
|
|
|
||
|
|
N k |
|
|
|
||
|
|
|
k 0 |
|
|
|
которая показывает, какой процент Р тестовых прогонов, необходимых для обнаружения всех N ошибок, был сделан, когда в процессе этих прогонов было найдено n ошибок. Если n=10, то по последней формуле получим, что половина всех ошибок может быть обнаружена в первых 22 % тестовых прогонов, необходимых для обнаружения всех ошибок. Процент прогонов возрастает до 37, если требуется найти 7 из 10 ошибок, и до 66, если требуется обнаружить 9 ошибок из 10, то есть третья часть времени затрачивается на обнаружение одной последней ошибки. Если в программе имеется 100 ошибок, то 90 обнаруживается за первые 44 % тестовых прогонов. Этот закон, устанавливающий, что эффект от тестирования уменьшается со временем, позволяет сделать вывод о необходимости прекращать тестирование в тот момент, когда оно становится эконо-
163
мически невыгодным. Кроме того, можно утверждать, что в отлаженном модуле почти всегда остаются ошибки.
5.7. Формальные методы доказательства правильности программ
Формальный подход к доказательству правильности программ заключается в использовании логики для демонстрации корректности программного модуля. Пользуясь этим подходом, можно показать, что модуль удовлетворяет заданным спецификациям, но нельзя определить, полон ли набор спецификаций и верны ли они. Считается, что модуль выполняется не на реальной машине, для которой характерно распространение ошибок и возникновение нестандартных ситуаций, а на гипотетической. Другими словами, текст программного модуля рассматривается как математическая модель его спецификаций, а не реальная программа для ЭВМ. Для формального доказательства корректности программист должен второй раз описать логику программы (первым описанием является текст самой программы). Это требует формального задания спецификаций. Таким путем осуществляется дополнительный контроль ошибок.
Доказательство правильности состоит из двух частей. Сначала показывается, что выполнение модуля обязательно завершится; затем с помощью определенных утверждений, связанных с входными переменными модуля, доказывается истинность других утверждений в момент завершения модуля. Для этого обычно используются формальные методы доказательства или неформальная аргументация. При использовании формальных методов удается избежать ошибок, свойственных неформальной аргументации, но эти методы менее удобны в том случае, если нужно убедить людей в корректности программы. Кроме того, проведение формальных доказательств достаточно утомительно.
164
|
|
|
|
5.7.1. Утверждения |
|
|
|
|
Первым шагом в процессе доказательства корректности |
||||||
модуля является задание формальных утверждений, касающих- |
|||||||
ся значений переменных в различных точках структурной схе- |
|||||||
мы программы, в частности в начале, конце, до и после точек |
|||||||
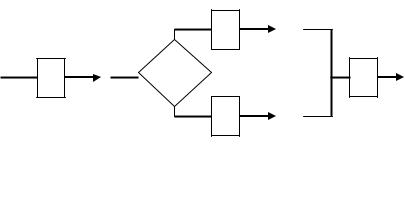
ветвления и слияния. На рис. 5.2 показаны основные способы |
|||||||
вывода утверждений для последовательностей операторов F и |
|||||||
G и утверждений Р, Q, R и S. Утверждение Q считается ис- |
|||||||
тинным, если логическая проверка q дает положительный ре- |
|||||||
зультат. Запись P{F}Q означает, что, если утверждение Р ис- |
|||||||
тинно и выполнена последовательность операторов F, утверж- |
|||||||
дение Q истинно[6]. |
|
|
|
|
|||
|
Утверждения могут быть сформулированы на любой |
||||||
стадий разработки программы. Если принят подход, основан- |
|||||||
ный на пошаговой детализации проекта, неформальные доказа- |
|||||||
тельства утверждений могут проводиться на каждой стадии де- |
|||||||
тализации. Формальные же методы доказательства можно ис- |
|||||||
пользовать только тогда, когда полностью готов текст про- |
|||||||
граммного модуля. |
|
|
|
|
|||
|
|
|
R |
|
F |
P |
|
|
|
|
|
|
|
|
|
P |
F |
S |
P |
Q |
|
F |
S |
|
|
|
|
|
F |
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S |
|
|
|
P{F}S |
|
|
|
( (P R){F}S |
||
|
(P Q){F}R |
(P ~Q){G}S |
|
|
|||
|
|
|
в |
|
|||
|
а |
|
|
|
б |
|
|
|
|
|
|
|
|
||
|
Рис. 5.2. Правила вывода утверждений для основных |
||||||
|
конструкций программы: а – следование, б – развилка, |
||||||
|
|
|
|
в – узел слияния |
|
|
|
165
Если в программе, вычисляющей наибольший общий делитель, предусмотрены входные и выходные спецификации, они могут считаться утверждениями для всей функции. На псевдокоде это записывается так:
Р: утверждается, что i, j имеют наибольший делитель, равный g,
F: вычисляется GCD (I,J) для I=i, J=j,
Q: утверждается, что GCD(i,j)=g.
Здесь прописными буквами обозначены переменные программы, а строчными - значения переменных. Все утверждения касаются значений, а не самих переменных. Утверждения должны быть сформулированы таким образом, что если Р истинно и выполнена программа F, то Q также истинно. В вышеприведенном примере Р не является истинным, если i и j равны нулю. Но в утверждениях не содержится ничего относящегося к этому случаю. Поэтому не считается неверным переход от Р к Q с помощью F. Таким образом, набор спецификаций неполон, и необходимо его расширить так, чтобы учесть вариант, когда определяется GCD (0, 0).
Расширим текст программы на псевдокоде, введя дополнительные утверждения, следующим образом:
Р: утверждается, что i, j имеют наибольший общий делитель, равный g,
F: N:=min (|I|, |J[);
M:=max(|I|, |J|);
R: утверждается, что g=gcd (i,j), g=gcd (n,m), 0 n m, G: вычисляется GCD (N,M) для N=n, M=m,
Q: утверждается, что GCD (i, j) = g.
Тогда задача определения наибольшего общего делителя двух чисел может быть сведена к более простой задаче определения наибольшего общего делителя двух упорядоченных по возрастанию неотрицательных чисел, т. е. P{F}Q может быть расширено до выражения P{F}R{G}Q, обе части которого имеют свои собственные спецификации. Чтобы показать корректность всей программы, необходимо показать, во-первых,
166
что если Р истинно и F выполнено, то R истинно, и, во-вторых, что Q следует из R и G. Описания для F и окаймляющих его утверждений могут быть расширены:
Р: утверждается, что i, j имеют наибольший общий делитель, равный g,
F: N:=abs(I);
M:=abs(J);
утверждается g=gcd (i,j), g=gcd (n,m), 0 n, 0 m
if N>M then поменять местами значения M и N,
R: утверждается, что g=gcd (i,j), g=gcd (n',m'), 0 n' m'.
Отметим, что значения М и N в R могут отличаться от значений, приписываемых этим переменным раньше. Так как n и m использовались для представления первоначальных значений N и М, то для представления этих переменных в R используются n' и т', причем либо n'=n и m'=m, либо n'=m и m'=n. Для детализации описания процедуры G введем цикл:
R: утверждается, что g=gcd (i,j), g=gcd (n',m'), 0 n' m G: while N<>0 do
утверждается, что g=gcd (i,j), g=gcd (n',m'), 0<n' m' L : = remainder (M, N);
M:=N;
N := L;
утверждается, что g=gcd (i, j), g=gcd (n", m"), 0 n" m" endwhile
утверждается, что g=gcd (i,j),m"=g GCD:=m" Q: утверждается, что GCD (i,j)=g.
Утверждения, стоящие в начале и в конце цикла, очень похожи. Новые значения n" и m" в конце цикла становятся n' и m' для следующей итерации. Утверждения, связанные с циклом, должны отражать отношения, которые являются истинными, независимо от того, сколько раз цикл выполняется. Эти неизменные отношения получили название инварианты цикла. Инвариант - это выражение, аналогичное выражению, приме-
167
няемому для рекурсивного определения функций, которое выражает текущие значения переменных через их предыдущие значения. Инвариант служит для описания связей значений, принимаемых переменными в течение одной произвольно взятой итерации, с предыдущими значениями тех же переменных. Отметим, что в этом случае для доказательства можно использовать индукцию.
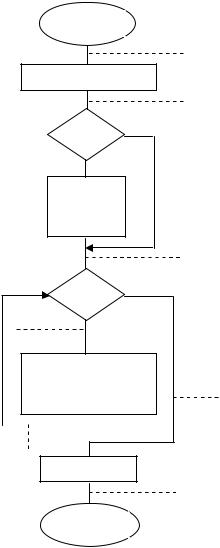
На рис. 5.3 показана структурная схема функции GCD, дополненная полученными утверждениями. Формальная запись программы принимает вид
A1{F1}А2(((n >m){F2}) ((n m){ })) А3, ((n' 0) А4|{F3}|А5)* (n' = 0) A6 {F4} А7.
168
Start
A1
F1 N I M J
A2
N<M
No Yes
K N
N M
F2 M K
A3
N=0
A4L IREM(M,N)
M N No
N L
|
|
A6 |
F3 |
|
GCD M
A5
F4 End
A7
Рис. 5.3. Структурная схема функции GCD 169
Корректность модуля подтверждается тем, что последовательное выполнение сегментов программы позволяет переходить от одного утверждения к следующему. Для наиболее глубоко лежащих структур порядок следования утверждений меняется на обратный. Правильность структуры выбора на рис. 19 может быть установлена, если удастся показать, что справедливо
A2(((n>m){F2}) ((n m){ }))А3,
т. е. сегмент F2 позволяет перейти от A2 к А3 при условии, что n>m, и А3 следует непосредственно из n m.
Для цикла необходимо проверить следующие утвержде-
ния:
А3(n'=0)А6, А3(n'' 0)A4, A4{F3}А5, А5(n' 0)А4 и А5(n'=0)А6.
После этого формальная запись текста программы примет вид
A1{F1}A2{G1}А3{G2}(n' = 0)А6{F4) А7.
причем известно, что G1, G2 — правильные сегменты. Тогда должны быть проверены только утверждения
A1{F1}A2 и А6{F4) А7.
5.7.2. Завершение выполнения модуля
Чтобы показать, что выполнение программного модуля дает верные результаты, недостаточно продемонстрировать его корректность. Необходимо также показать, что выполнение модуля приведет в то место (точку) программы, где эти результаты получаются. Выполнение будет достигать заранее определенной точки, если, во-первых, точка принадлежит всем путям, проходящим через модуль, во-вторых, все циклы заканчиваются и, в-третьих, в этом модуле или в других, вызываемых им, не возникает исключительных ситуаций, попадание в которые приводит к нестандартному завершению выполнения модуля [7]. В случае программы GCD существует только одна такая ситуация: имеется в виду вызов функции, вычисляющей оста-
170
