Базы данных материалов для САПР в машиностроении. Елисеев В.В., Хливненко Л.В

Рис. 1.14

После нажатия на кнопку ОК на листе останутся только строки с максимальным усилием, как показано на рис. 1.15.

Рис. 1.15

Запишите номер строки с максимальным усилием и отмените результаты фильтрации по команде Ctrl+Z.

В блоке A2:С2159 поставим ссылки на ячейки с данными T2:V2159. Для этого в ячейке A2 следует указать ссылку =T2 и нажать Enter. Затем копируем формулу в ячейки B2 и C2, потянув за черную точку в правом нижнем углу ячейки A2

(рис.1.16).

Рис.1.16

Выделив блок A2:C2, скопируйте его в буфер обмена. Затем, выделив блок A2:C2159, вставьте формулы из буфера. Для быстрого выделения данных используйте Ctrl+Shift+.

Вставьте в книгу 1-0.xls новый лист (правый клик по ярлыку листа data) и назовите его dl-P. На этом листе

20

разместим диаграмму деформирования в координатах удлинение ( l ), растягивающее усилие (P ) по команде

Вставка Точечная диаграмма с гладкими кривыми.

Изменить диапазон данных на диаграмме можно через меню Конструктор с помощью инструмента Выбрать данные (рис. 1.17).

Рис. 1.17

Укажите в качестве источника данных диапазон A2:B5000

(рис. 1.18).

Рис. 1.18

21

В результате на листе dl-P появится экспериментальная диаграмма деформирования, показанная на рис. 1.19.

Конец кривой не должен содержать изломов и должен представлять собой плавную линию. Если изломы есть, то удалите несколько последних строк с данными.

Рис. 1.19

1.4. Лабораторная работа № 3 Определение предельных деформаций листовых материалов при растяжении в условиях плоской

деформации

Цель работы: изучить метод экспериментального определения предельных деформаций листовых материалов для прогнозирования технологических отказов в операциях листовой штамповки.

1.4.1. Теоретическая справка

Одним из доминирующих технологических дефектов (отказов) операций листовой штамповки является потеря

22

устойчивости в виде местных утонений, по которым затем происходит разрыв материала. Для прогнозирования потери устойчивости листовой заготовки в процессе пластического формообразования используют диаграмму предельных деформаций (ДПД).

Диаграмму строят в координатах: наибольшая главная деформация в плоскости листа e1* и параметр вида

деформированного состояния e2 /e1*, где e2 - наименьшая главная деформация в плоскости листа. На рис. 1.20 приведена типичная ДПД алюминиевого сплава Д16АМ.

Для оценки предельных возможностей заготовки при штамповке на каждом этапе формообразования определяют наибольшие главные деформации e1,e2 в плоскости листа и рассчитывают . Если точка на координатной плоскости ДПД, соответствующая деформированному состоянию заготовки, лежит ниже диаграммы, считают, что в рассматриваемый момент времени процесс ведется бездефектно (рис.1.20).

e1*,%

10

e1 e1*

e1 ,

Рис. 1.20

23

На рис. 1.20 показано, что минимальная предельная деформация наблюдается при плоской деформации. При этом e2 0, 0 .

Для построения левой ветви ДПД проводят два вида испытаний: на одноосное растяжение, рассмотренное в лабораторной работе №1.1, и на растяжение в условиях плоской деформации.

1.4.2. Испытание

1.4.2.1. Образец

Испытывают приталенные образцы на растяжение (рис.1.21). Криволинейные боковые поверхности рабочей части позволяют реализовать вблизи оси образца в процессе растяжения деформированное состояние, близкое к плоскому.

Направление прокатки

R50.2

190

Рис. 1.21

1.4.2.2. Подготовка образца к испытанию

Подготовка образцов к испытанию. На рабочую поверхность образца наносят сетку из систем окружностей диаметром 2 3 мм (рис. 1.22).

24

Увеличено

2,7

0,2

10 10

Рис. 1.22

1.4.2.3. Процедура испытания

Образец растягивается до разрушения в испытательной машине. После разрушения измеряют наименьший l2 и наибольший l1 диаметры 5-7 круглых ячеек вдоль оси образца, чтобы уменьшить влияние градиентов деформаций на краях образца. Измерения производят в областях, прилегающих к трещине с обеих сторон на ширину образца (рис. 1.23). По результатам измерений строят зависимость распределения наибольшей деформации e1 ячейки от ее расстояния до трещины s (рис. 1.24).

20 20

Рис. 1.23

25

Размеры ячейки определяют под микроскопом с точностью 0.001 мм. По мере удаления от трещины деформация e1 уменьшается сначала интенсивно в области шейки (в области потери устойчивости), а затем после стабилизации - незначительно. Деформация e1 заштрихованной ячейки или нескольких ячеек, соответствующая границе перехода из зоны возмущения в зону стабильности (точка излома на графике распределения деформаций), используется затем для определения предельной деформации устойчивости в условиях, близких плоской деформации. По результатам испытаний одного образца определяют 2-4 значения предельной деформации устойчивости.

e1

s

Рис. 1.24

1.4.3. Обработка результатов измерений

Сначала вычисляют минимальные деформации e2 в этих ячейках (заштрихованная ячейка на рис. 1.24) и параметр вида деформированного состояния для последующего построения диаграммы предельных деформаций. Деформации выделенной i-й ячейки и параметр вида состояния вычисляют по формулам:

26

где l0 – диаметр исходной ячейки сетки образца, l1, l2 – соответственно наибольшая и наименьшая диагонали ячейки разрушенного образца (рис. 1.25).

l1

l0

l2

Рис. 1.25

Предельная деформация устойчивости при плоской деформации вычисляется в результате экстраполяции диаграммы предельных деформаций, полученной по результатам испытаний на одноосное растяжение и растяжение в условиях, близких к плоской деформации.

Для этого на поле диаграммы (в координатах предельная деформация устойчивости в направлении растяжения e1 и

27

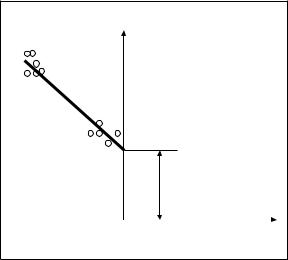
параметр вида деформированного состояния ) наносят точки, соответствующие предельной деформации устойчивости в условиях одноосного растяжения и плоской деформации из предыдущих опытов (рис. 1.26). Предельная деформация устойчивости в условиях плоской деформации при растяжении в направлении e(*0)0 и поперек e(*0)90 прокатки является точкой

пересечения этой ветки диаграммы с осью ординат.

e1

e(*0 ) 0 (e(*0 ) 9 0 )

Рис. 1.26

Аналитически предельная деформация устойчивости определяется методом наименьших квадратов:

( j )2 (n m) ( j )2

j 1

28

где (n+ m) – число ячеек, в которых измеряли деформации соответственно в испытаниях на одноосное растяжение n и на плоскую деформацию m в одном направлении к прокатке.

Результаты расчетов вносят в табл. 1.4.

29