Добавил:

mihail1000 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Воронежский государственный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Учебное пособие 1174

.pdf

Скачиваний:

Добавлен:

30.04.2022

Размер:

839.07 Кб

Скачать

☆

<<< < Предыдущая 1 2 34 / 64 5 6 > Следующая >>>

																					(c − λ									u − 1)2														(c − λ												u − 1)3
(c − λ									u − 1)							−							2						2													+						2						2
(c − λ							2		u − 1)							−																										+
			2				2																						2																									3
														= u2													λ22
																							(−									) + u(λ											c				− 2λ							2	) −
																							(−									) + u(λ											c				− 2λ								) −
																													2													2		2
																													2
	(c				− 1)2																														λ		3
−			2									+ c − 1 + u3 (−																							2			) + u2(λ2(c − 1)) +
−												+ c − 1 + u3 (−																										) + u2(λ2(c − 1)) +
						2							2																						3																	2			2
						2																													3
										+u(−λ											(c − 1)2) +																(c			2		− 1)3										=
										+u(−λ											(c − 1)2) +																															=
																		2					2																			3
																				λ23																						3
																				λ23
									= u3 (−															) + u2(λ2(c																		− 1,5)) +
									= u3 (−															) + u2(λ2(c																		− 1,5)) +
																					3														2		2
																					3
																																		(c			− 1)2														(c		2	− 1)3
+u (λ	((c					− 2) − (c												− 1)2)) −																	2										+								2							+ c − 1.
+u (λ	((c					− 2) − (c									2			− 1)2)) −																											+															+ c − 1.
2			2												2																						2																	3							2
																																					2																	3
Сгруппируем слагаемые относительно u:
			Г(c )															λ	c1																							3							u			2								11
			Г(c )															λ																							u								u											11
ln (−						2		) + ln (											1			) + (c								− c							) (							−									+ 3u −								) +
ln (−				Г(c1)				) + ln (														) + (c								− c							) (							−									+ 3u −								) +
				Г(c1)														λc2											1						2							3								2										6
																			2									λ 3
																												λ 3
			+u(λ							− λ )					+ u3								(−						1				) + u2(λ2(c																			− 1,5)) +
			+u(λ				2			− λ )					+ u3								(−										) + u2(λ2(c																			− 1,5)) +
							2						1																3														1					1
																													3
																																														(c						− 1)2
				+u (λ ((c											− 2)								− (c							− 1)2)) −																		1										+
				+u (λ ((c											− 2)								− (c							− 1)2)) −																												+
									1				1																1																							2
					− 1)3																														3																	2
		(c			− 1)3																										λ				3
+			1									+ c						− 1 + u3 (															2			) + u2(λ2(1,5 − c																								)) +
+												+ c						− 1 + u3 (																		) + u2(λ2(1,5 − c																								)) +
						3							1																				3															2									2
						3																											3
											((c				− 1)2 − (c																			− 2))) +												(c				2		− 1)2
				+u (λ																																														2									−
				+u (λ																																																							−
									2				2																2																							2
																			(c				− 1)3																													2
																			(c				− 1)3
														−							2											− c + 1 =
														−																		− c + 1 =
																									3										2
																									3																													± λ 3
								Г(c					)													λc1													c − c λ														3	± λ 3
											2														1				) + u3											1								2				2					1
= ln (−														) + ln (																							(																							) +
= ln (−								Г(c1)						) + ln (												λc2											(													3										) +
																									2
				+u2 (						c1 − c2							+ λ2(c												− 1,5) + λ2(1,5 − c																												)) +
				+u2 (													+ λ2(c												− 1,5) + λ2(1,5 − c																										2		)) +
											2										1				1																	2													2
											2

	+u(		3c1 − 3c2					+ λ ((c − 2) − (c							− 1)2		− 1) +
	+u(							+ λ ((c − 2) − (c							− 1)2		− 1) +
					2				1		1	1
					2		((c		− 1)2		− (c	− 2) + 1)) −
				+λ			((c		− 1)2		− (c	− 2) + 1)) −
						2	2				2
	(c − 1)2			(c	2	− 1)2				(c	− 1)3		(c	− 1)3				5		5
−	1	+			2				+	1		−	2			−			c +		c = 0.
−	2	+				2			+		3	−		3		−		6	c +	6	c = 0.
	2					2					3			3				6	1	6	2

Введем замену переменных:

			Г(c		)							λc1		(c			− 1)2						(c			− 1)2
d = ln (−			2			) + ln (						1	) −		1						+				2		+
d = ln (−			Г(c1)			) + ln (						λc2	) −								+						+
12			Г(c1)									λc2						2								2
		(c − 1)3									2		− 1)3
		(c − 1)3									(c		− 1)3					5				5
+			1					− −			2					−			c +					c ,
+			3					− −					3			−		6	c +			6		c ,
			3										3					6		1		6			2
										c	− c λ 3				± λ 3
				a12 =						1			2 2					1		,
				a12 =									3							,
				c1 − c2									3
b =				c1 − c2				+ λ2(c − 1,5) + λ2(1,5 − c																		),
b =								+ λ2(c − 1,5) + λ2(1,5 − c																		),
12			2						1		1								2						2
c =	3c1 − 3c2						+ λ ((c						− 2) − (c							− 1)2					− 1) +
c =							+ λ ((c						− 2) − (c							− 1)2					− 1) +
12			2						1		1							1
			2		((c				− 1)2 − (c						− 2) + 1).
				+λ	((c				− 1)2 − (c						− 2) + 1).
			2			2							2

Таким образом, получаем уравнение:

a12u3 + b12u2 + c12u + d12 = 0.

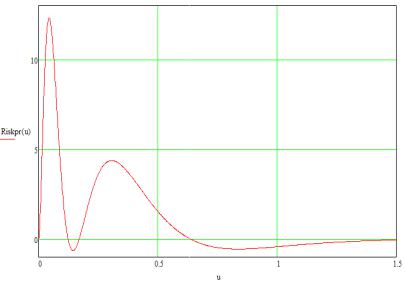
График функции производной риска представлен на рис. 6, где пересечения с осью ущербов соответствуют экстремумам функции.

Рис. 6. Вид функции производной риска

Решением уравнения

вышеприведенного

уравнения

является выражение:

с1

+ r

λ1

где

r12 − поправка,

вносимая

первое

решение

второй

компонентой.

Поправку r12 определим следующим образом:

λc1 (с1 + r

)c1−1 exp (−λ (с1 + r

))

(c − λ (

+ r

)) +

Г(c )

λc2

(с1

+ r

)c2−1 exp (−λ

(с1

+ r

))

(c − λ

(

+ r )) = 0.

Г(c

)

Упростим данное уравнение подобно уравнению производной риска и, таким образом, получим:

a12u13 + b12u12 + c12u1 + d12 = 0.

Разделим уравнение на a12:

b12	u2	+	c12	u +	d12	= 0.

a12 1			a12 1		a12

Уравнение подобного вида решается с помощью теоремы Виета.

Вычисляем:
			(b12)2			− 3 c12
	=		a12				a12		,
	=			b912					,
	2(b12)3 − 9			b912			c12	+ 27 d12
	2(b12)3 − 9						c12	+ 27 d12
=	a12			a12 a12					a12	,
=					54					,
					54
		= 3				− 2.

Если все коэффициенты кубического уравнения вещественны, то и S вещественно, и по его знаку можно определить тип корней:

S > 0 – три вещественных корня;

S = 0 – один однократный вещественный корень и один двукратный;

S < 0 – один действительный корень и пара комплексно сопряженных.

Следовательно, при S > 0 получаем 3 вещественных

корня u11, u12, u13:

u = −2√Q

cos(ϕ) −

b12

3a12

= −2√Q

cos (ϕ +

π) −

b12

3a12

= −2√Q

cos (ϕ −

π) −

b12

3a12

где ϕ = 13 arccos (√RQ3).

Данные корни будут определять 3 поправки

r12(1), r12(2), r12(3).

r(1)	= u	−	с1	,
12	11		λ
			с1
r(2)	= u	−	1	,
r(2)	= u	−	λ	,
12	12		λ
			с1
r(3)	= u	−	1	.
r(3)	= u	−		.
12	13		λ1
			λ1

Минимальная и максимальная поправки определяют максимумы функции риска, что видно из рис. 7, иллюстрирующего данный случай. Минимум же определяет поправка, которая находится между минимальной и максимальной поправками.

Рис. 7. Интегральная оценка риска РКС, состоящей из двух компонентов и имеющей три экстремума

Возможен случай, когда расстояние между модами рисков двух компонент РКС невелико (рис. 8). Для данного случая выполняется условие S = 0 и уравнение производной риска будет иметь один вещественный корень, который

попадает в интервал (с1 , с2 ).

λ1 λ2

Корень уравнения при этом равен одному из корней:

u1 = −23√R − b12 , 3a12 u1 = 23√R − b12 . 3a12

Рис. 8. Интегральная оценка риска РКС, состоящей из двух компонентов и имеющей один экстремум

Рассмотрим случай, когда система состоит из n компонентов.

При этом первый максимум смещается вправо в результате действия поправок от других компонент.

При этом поправки можно определить как:
r(1)	= u	−	с1	,
r(1)	= u	−	λ	,
1i	i1		λ
			с1
r(2)	= u	−	1	,
r(2)	= u	−	λ	,
1i	i2		λ
			с1
r(3)	= u	−	1	.
r(3)	= u	−		.
1i	i3		λ1
			λ1
При этом на	максимум			влияют	только

min(r1i(1), r1i(2), r1i(3)).

Для второго максимума первый максимум сдвигает его влево, остальные вправо.

В результате получаем, что:

r21(1)	=	с2	− u21	,
		λ2
		с
r21(2)	=	2	− u22	,
		λ2
		с
r21(3)	=	2	− u23.
		λ2

Для i >2 поправки имеют следующий вид.

r(1)	= u		−	с2	,
r(1)	= u	i1	−		,
2i		i1		λ2
				λ2
				с
r(2)	= u		−	2	,
r(2)	= u	i2	−		,
2i		i2		λ2
				λ2
				с
r(3)	= u		−	2	.
r(3)	= u	i3	−		.
2i		i3		λ2
				λ2

Тогда для i-го компонента получаем:

				сi	− u			,
					− u			,
	(1)			λi			j1
r	(1)	= {		λi			сi
r	ij	= {
	ij		u			−		,


				j1			λi
				сi			λi
				сi	− u			,
					− u			,
	(2)			λi			j2
r	(2)	= {		λi		− сi ,
r	ij	= {	u
			u

				j2
				j2			λi
				сi			λi
				сi	− u			,
					− u			,
	(3)			λi			j3
r	(3)	= {		λi		− сi ,
r	ij	= {	u
			u

j3 λi

> ;

< .

> ;

< .

> ;

< .

При этом для ущерба, аналогично поправкам определяем знак поправки, следующим образом:

	сi	+ r ,	> ;
		+ r ,	> ;
	λi	ij
u = {	λi
u = {	сi
ij	сi	− r ,	< .
		− r ,	< .
	λi	ij
	λi

Для случая асинхронных атак, атака на отдельный компонент РКС не влияет на работоспособность другого компонента системы, а риск распределенной системы в целом определяется как сумма рисков компонент и, следовательно, компоненты можно рассматривать как независимые.

Таким образом, ущербы, определяющие максимумы риска, выражаются следующим образом:

u1 = λс1 + min(r12(1), r12(2), r12(3)) + + min(r1n(1), r1n(2), r1n(3)), 1

u = −min(r(1), r(2)

, r(3)) +

с2

+ + min(r(1)

, r(2), r(3)),

λ2

сn

= −min(r(1)

, r(2)

, r(3)) − − min(r(1)

, r(2)

, r(3)

) +

n(n−1)

λn

Введем обозначение r(min) = min(r(1), r(2), r(3)).

Для удобства данные поправки можно записать в виде

матрицы:

−0

−r(min)

−

r(min)

D =

− − r21(min)

−

r2n(min) .

…

− …

−

( −rn1(min)

−rn2(min)

− …

−0

)

Сумма элементов в i-ой строке определяет поправку для

моды ущерба i-го компонента.

ui = λсi + ∑ rij(min). i j=1

Таким образом, получается вектор координат ущербов, при которых функция суммарного риска имеет максимум:

с1

λ1

сi

U = λi

сn

(λn

+ ∑ r1j(min)

j=1

+ ∑ rij(min) .

j=1

+ ∑ rnj(min) j=1 )

Рассмотренный выше случай предполагает, что кубическое уравнение имеет три вещественных корня. Если же решение уравнения имеет один корень, то два максимума объединяется в один. Для совпадающих максимумов в i-1 и i компонентах вектор будет иметь следующий вид:

			n
		с1 + ∑ r(min)
		λ1	1j
		λ1	j=1
			j=1

			n
	сi−1 + ∑ r(min)
	λi−1		ij
	λi−1		j=1
U =			j=1
U =			n
	сi+1 + ∑ r(min)

λi+1 j=1 ij

сn + ∑ r(min) ( λn j=1 nj

)

Итоговую поправку для минимума, используя данный подход определить, не представляется возможным, поэтому для их нахождения можно использовать численные методы, например, метод Ньютона.

<<< < Предыдущая 1 2 34 / 64 5 6 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
30.04.2022286.32 Кб2Учебное пособие 117.pdf
#
30.04.2022837.63 Кб3Учебное пособие 1170.pdf
#
30.04.2022838.58 Кб3Учебное пособие 1171.pdf
#
30.04.2022838.88 Кб3Учебное пособие 1172.pdf
#
30.04.2022838.97 Кб5Учебное пособие 1173.pdf
#
30.04.2022839.07 Кб3Учебное пособие 1174.pdf
#
30.04.2022840.55 Кб2Учебное пособие 1175.pdf
#
30.04.2022841.41 Кб20Учебное пособие 1176.pdf
#
30.04.2022841.9 Кб4Учебное пособие 1177.pdf
#
30.04.2022843.01 Кб4Учебное пособие 1178.pdf
#
30.04.2022843.4 Кб3Учебное пособие 1179.pdf