Учебное пособие 1034

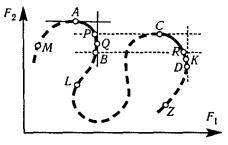
Рис. 5. Изменение множества эффективных решений

Варианты заданий

В пространстве критериев нарисовать точки, соответствующие отдельным вариантам решений. Найти точки, составляющие множество Парето.

Вариант 1. Критерий F1 – эффективность вариантов решений, критерий F2 – экономия времени при решении проблемы.

Вариант 2. Критерий F1 – прибыль от реализации вариантов решений, критерий F2 – время решения проблемы.

Вариант 3. Критерий F1 – затраты на реализацию вариантов решений, критерий F2 – время решения проблемы.

Вариант 4. Критерий F1 – время решения проблемы, критерий F2 – экономия средств при реализации вариантов решений.

Вариант 5. Критерий F1 – экономия времени при решении проблемы, критерий F2 – затраты на реализацию вариантов решений.

Из таблицы случайных чисел, полученных у преподавателя, выбрать по 10 значений для каждого критерия.

Например, студент гр. МП – 3, 35-й по списку, выбирает следующие исходные данные:

РЕШЕНИЕ ЗАДАЧ МНОГОКРИТЕРИАЛЬНОЙ ОПТИМИЗАЦИИ МЕТОДОМ ПОСЛЕДОВАТЕЛЬНЫХ УСТУПОК

Впрактической деятельности часто встречаются задачи, заключающиеся

впоиске лучшего (оптимального) решения при наличии различных несводимых друг к другу критериев оптимальности. Например, принятие решения о строительстве дороги в объезд города должно учитывать такие факторы, как выигрыш города в целом по соображениям экологии, проигрыш отдельных пред-

11

приятий и фирм, например, из-за уменьшения проезжающих через город потенциальных покупателей и многие другие. Если такого рода задачи решаются методами математического программирования, то говорят о задачах многокритериальной оптимизации. Эти задачи могут носить как линейный, так и нелинейный характер. Поскольку методы решения таких задач излагаются ниже на примере линейных многокритериальных оптимизационных задач, это объясняет рассмотрение этой темы в данной главе учебного пособия.

Задачи многокритериальной оптимизации возникают в тех случаях, когда имеется несколько целей, которые не могут быть отражены одним критерием (например, стоимость и надежность). Требуется найти точку области допустимых решений, которая минимизирует или максимизирует все такие критерии. Если в подобного рода задачах речь идет не о разнородных критериях некоторой системы, а о сопоставлении однородных критериев разных ее подсистем (например, отрасли, группы населения и т.п.), то эти задачи называются задачами векторной оптимизации.

Обозначим i-й частный критерий через Zi( X), где Х - допустимое решение, а область допустимых решений - через Q. Если учесть, что изменением знака функции всегда можно свести задачу минимизации к задаче максимизации, то кратко задачу многокритериальной оптимизации можно сформулировать следующим образом:

Некоторые частные критерии могут противоречить друг другу, другие действуют в одном направлении, третьи - индифферентны, безразличны друг к другу. Поэтому процесс решения многокритериальных задач неизбежно связан с экспертными оценками как самих критериев, так и взаимоотношений между ними. Известен ряд методов решения задач многокритериальной оптимизации:

– оптимизация одного признанного наиболее важным критерия, остальные критерии при этом играют роль дополнительных ограничений;

упорядочение заданного множества критериев и последовательная оптимизация по каждому из них (этот подход рассмотрен ниже на примере метода последовательных уступок);

сведение многих критериев к одному введением экспертных весовых коэффициентов для каждого из критериев таким образом, что более важный критерий получает более высокий вес.

Возвращаясь к задаче многокритериальной оптимизации в общей постановке (1), (2), отметим, что в идеальном случае можно вести поиск такого решения, которое принадлежит пересечению множеств оптимальных решений всех однокритериальных задач. Однако такое пересечение обычно оказывается пустым множеством, поэтому приходится рассматривать так называемое «переговорное множество эффективных решений (оптимальных по Парето). Крите-

12

рий оптимальности итальянского экономиста В.Парето применяется при решении таких задач, когда оптимизация означает улучшение одних показателей при условии, чтобы другие не ухудшались.

Определение. Вектор 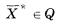называется эффективным (оптимальным по Парето) решением задачи (1), (2), если не существует такого вектора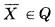, что

причём хотя бы для одного значения i имеет место строгое неравенство. Множество допустимых решений, для которых невозможно одновремен-

но улучшить все частные показатели эффективности (т.е. улучшить хотя бы один из них, не ухудшая остальных), принято называть областью Парето, или областью компромиссов, а принадлежащие ей решения эффективными, или оптимальными по Парето.

Вобщем случае эффективные решения не эквивалентны друг другу, так что про два оптимальных по Парето решения нельзя сказать, какое из них лучше. Поэтому при решении многокритериальных задач необходимо дополнительное изучение эффективных решений. Для этого можно было бы сформулировать некоторый критерий и оптимизировать его на множестве эффективных решений. Однако при этом возникают значительные трудности в связи с тем, что, как правило, область компромиссов не является выпуклой, и полученная задача в общем случае будет задачей невыпуклого программирования. Обычный подход заключается в стремлении «свернуть частные критерии в один обобщенный скалярный критерий, оптимизация которого приводит к оптимальному решению задачи в целом. Формулировка подходящего обобщённого критерия в зависимости от конкретных условий как раз и является основным вопросом, который изучается в многокритериальной оптимизации.

Внекоторых случаях вместо одного обобщённого критерия и решения одной соответствующей задачи скалярной оптимизации предлагается рассматривать последовательность обобщённых критериев и последовательность задач скалярной оптимизации. К сожалению, многие из описанных в литературе подобных процедур не всегда приводят к эффективным решениям.

Рассмотрим один из таких методов решения многокритериальных задач: метод последовательных уступок.

Метод последовательных уступок решения задач многокритериальной оптимизации применяется в случае, когда частные критерии могут быть упорядочены в порядке убывания их важности. Предположим, что все частные кри-

терии максимизируются и пронумерованы в порядке убывания их важности. Находим максимальное значение Z1* первого по важности критерия в области допустимых решений путем решения однокритериальной задачи

13

Затем, исходя из практических соображений и принятой точности, назначается величина допустимого отклонения δ1 > 0 (экономически оправданной уступки) критерия Z1 и находится максимальное значение второго критерия при условии, что значение первого критерия не должно отклоняться от своего максимального значения более чем на величину допустимой уступки, т. е. решается задача:

Снова назначается величина уступки δ2 > 0 по второму критерию, которая вместе с первой уступкой используется для нахождения условного максимума третьего частного критерия:

Аналогичные процедуры повторяются до тех пор, пока не будет выявлено максимальное значение последнего по важности критерия Zm при условии, что значение каждого из первых m – 1 частных критериев отличается от соответствующего условного максимума не более чем на величину допустимой уступки по данному критерию. Полученное на последнем этапе решение считается оптимальным. Следует заметить, что этот метод не всегда приводит к эффе ктивному решению.

Пример решения задачи многокритериальной оптимизации методом последовательных уступок.

Пусть задача трехкритериальной оптимизации имеет вид:

Для определенности будем считать, что допустимые уступки по первым двум критериям заданы: δ1= 3; δ2= 5/3.

Максимизируем функцию Z1 в области допустимых решений, т. е. решаем однокритериальную задачу (3), (6). Это несложно сделать графическим методом решения задач линейного программирования (рис. 6).

14

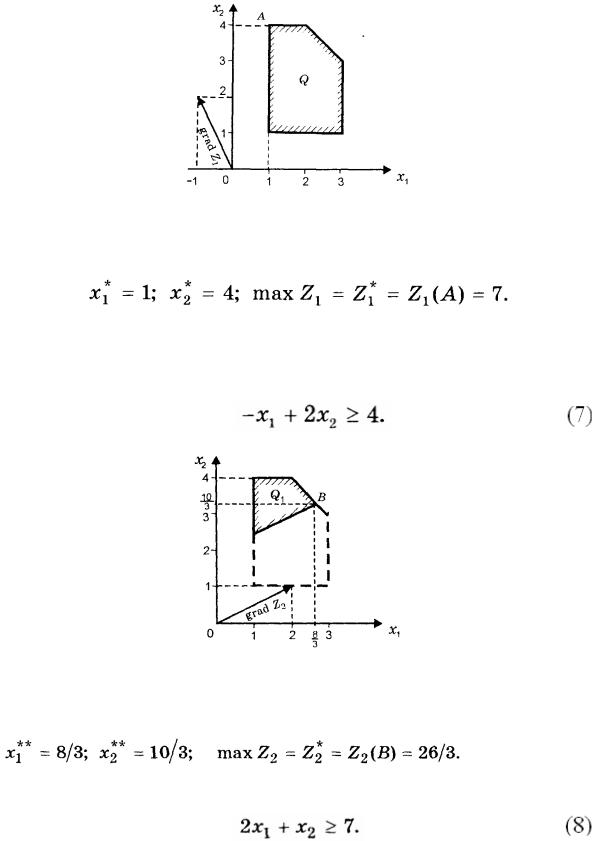
Рис. 6. области допустимых решений

Максимум функции Z1 при условиях (6) достигается в точке А области Q с координатами (1;4), так что в данном случае

Переходим к максимизации функции Z2 при условиях (6) и дополнительном ограничении, позволяющем учесть, что по критерию Z1 нельзя уступать более чем на δ1. Так как в нашем примере Z1*- δ1= 4, то дополнительное ограничение будет иметь вид:

Задачу (4), (6), (7) также решаем графически (рис. 7).

Рис. 7. Оптимальное решение по первому критерию

Получаем, что максимум функции Z2 при условиях (6), (7) достигается в точке В части Q1 области Q, так что

Теперь уступаем по критерию Z2 на величину уступки δ2= 5/3 и получаем второе дополнительное ограничение:

Максимизируем функцию при условиях (6), (7) и (8). Решение этой задачи графическим методом представлено на рис. 8.

15

Рис. 8. Оптимальное решение по второму критерию

Таким образом, получаем оптимальное решение рассматриваемой трехкритериальной задачи (точка С на рис. 8):

Соответствующие значения частных критериев при этом составляют:

Варианты заданий

Найти компромиссное решение, учитывая, что оптимальное решение должно удовлетворять величине, составляющей не менее 65% от значения, достигнутого по первому критерию.

16

МЕТОД АНАЛИЗА ИЕРАРХИЙ

При принятии решений часто воздействие той или иной альтернативы не может быть выражено количественно, или же количественная оценка такого влияния представляется в виде широкого диапазона значений показателей, что не снимает фактора неопределенности решения. Кроме того, имеется ряд факторов, оцениваемых не абсолютными, а ранговыми (порядковыми) показателями.

Определение целей с помощью многих показателей дает возможность принимать решения на базе нескольких критериев, т.е. с ориентацией на множество целей.

Чтобы повысить рациональность принятия решений и расширить возможности человека в области обработки информации, необходимо провести декомпозицию сложной проблемы на более простые частные задачи. На это и ориентирован метод анализа иерархий (аналитико-иерархический процесс). Метод базируется на обработке порядковой, т.е. “мягкой” информации, поступающей в распоряжение лица, принимающего решения (ЛПР), и на основе этой неполной информации позволяет определить ряд альтернативных вариантов решения.

Система целей для принятия решений не всегда имеет конкретную форму, кроме того, сначала необходимо разработать целевые показатели, требующиеся для принятия решения. В ходе последовательного выявления и формулирования главных целей через определение целей более низкого порядка (подцелей) создается иерархическая целевая система. При этом требуется также установить различия в важности целей одного иерархического уровня. Однако с ростом числа критериев, учитываемых при оценке альтернативных вариантов решений, уменьшаются способности ЛПР в области анализа проблем.

Метод анализа иерархий (МАИ) может быть использован в принятии решений следующим образом: после того как фактор неопределенности решаемой проблемы оценен в форме различных сценариев развития внешней среды, проводится сопоставление пар этих сценариев с помощью порядковой шкалы для установления вероятности осуществления того или иного сценария. Такая шкала представлена в табл. 1.

17

Данная таблица используется для построения иерархии целей путем ответа на вопрос: какая из каждых двух сравниваемых подцелей важнее для достижения цели более высокого уровня. В результате возникает горизонтальный ряд. Путем порядковой оценки определяется, какая из каждых двух сравниваемых альтернатив предпочтительнее для наилучшего достижения поставленной цели. Полученные данные попарного сравнения сценариев, целей и альтернатив решений оформляются в виде матриц.

При сопоставлении двух объектов анализа выбирается соответствующее значение шкалы Vij, сравнение этих же объектов в обратном порядке должно оцениваться обратной величиной Vji = 1 / Vij . Например, если менеджеры оценивают цель (Ц1) “лидерство фирмы в области качества” как “несколько важнее” по сравнению с целью (Ц2) “лидерство фирмы в области издержек”, то сопоставление в обратном порядке дает оценку “несколько неважнее”. Соответствующие значения по шкале будут V12=3 и V21=1/3.

Поскольку диапазон оценок шкалы ограничен, то оценочные суждения могут оказаться инконсистентными. Если, например, менеджмент поставит перед собой наряду с уже названными целями еще и цель (Ц3) “защита окружающей среды” и при этом для менеджмента лидерство в издержках “намного важнее” (Vij=7) по сравнению с добавленной целью, то консистентной оценкой для сопоставления важности целей “лидерство в издержках” и “защита окружающей среды”, следовало бы взять показатель Vij, равный 21. Однако он не согласуется с предложенной шкалой, где максимальной является величина 9.

На базе парного ранжирования сценариев развития внешней среды и сравнительных суждений о каждой паре целей и стратегий с помощью МАИ можно количественно рассчитать вероятность этих сценариев, веса целей и приоритеты альтернативных вариантов решений.

Для расчета необходимо полностью заполнить матрицу попарных сравнений, учитывая, что Vij=1/Vji . Для каждой строки матрицы рассчитывается среднее геометрическое значение gi и значимость (вероятность) альтернативы pi как отношение соответствующей средней геометрической к сумме всех среднегеометрических оценок G.

18

Для каждого столбца матрицы определяется сумма оценок sj .

Таблица 2

Матрица оценок попарного сравнения альтернатив

Сумма произведений полученных суммарных оценок sj и соответствующих значений вероятностей (приоритетов) позволяет определить максимальное собственное значение матрицы, которое должно быть не меньше, чем размерность матрицы λmax ≥ n :

n

λmax = ∑sj pi для i = j . j =1

Коэффициент согласованности или инконсистентности (КИ) определяется следующим образом:

КИ = λmaxn −−1n .

МАИ позволяет сблизить инконсистентные данные с консистентными. Если коэффициент инконсистентности превышает критическое значение КИ>0,1 , то менеджеры должны пересмотреть свои основные оценки.

Для проверки согласованности мнений экспертов определяется отношение согласованности ОС, как частное от деления коэффициента инконсистентности на величину случайной согласованности Сс, получаемую из специальных таблиц (табл. 3):

ОС = КИСс .

Считается приемлемым, если ОС ≤ 10%, допустимым, если ОС ≤ 20%, но если ОС > 20%, то оценки Vij необходимо пересмотреть.

19

Таблица 3

Значения величины случайной согласованности

Построить графическую структуру иерархии целей и альтернатив. Оценить в качестве эксперта значимость целей и альтернатив с помощью метода анализа иерархий. Проранжировать альтернативы согласно расчета их значимости и выбрать наиболее предпочтительную альтернативу.

Вариант 1.

Цель – получение выгоды от реконструкции предприятий. Критерии – прибыль, занятость, конкурентоспособность.

Альтернативы – тракторный завод, завод буровой техники, молочный завод.

Вариант 2.

Цель– получениевыгодыотразвитияспортивно-оздоровительногокомплекса. Критерии – привлечение инвестиций, занятость подростков, здоровье на-

селения.

Альтернативы – хоккейное поле, бассейн, теннисный корт.

Вариант 3.

Цель – получение выгоды от создания научного центра.

Критерии – новые технологии, образование, международные контакты. Альтернативы – центр доступа к Интернету, институт разработки новых

информационных технологий, центр социально-экономического прогнозирования развития региона.

Вариант 4.

Цель – получение выгоды от развития транспортного обслуживания. Критерии – быстрая прибыль, рабочие места, экология. Альтернативы – метро, троллейбусы, маршрутные такси.

Вариант 5.

Цель – создание эффективного предприятия в регионе.

Критерии – возможность получения земельного участка, наличие квалифицированного персонала, близость материальных ресурсов.

Альтернативы – нефтеперерабатывающее предприятие, автомобилестроительный завод, лесоперерабатывающая фабрика.

20