Учебное пособие 1033

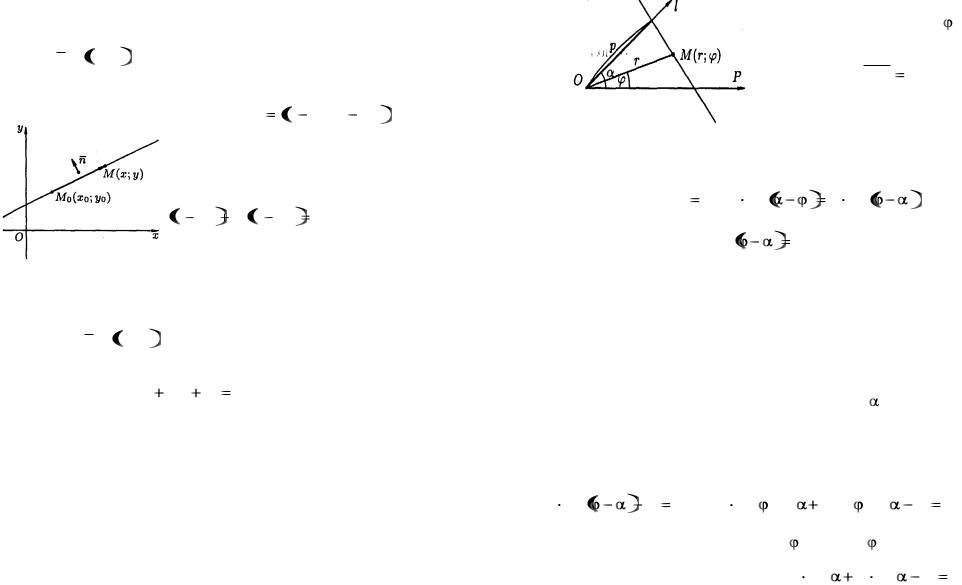
точку перпендикулярно данному вектору

Найдем уравнение прямой, проходящей через заданную точку Мо(хо;уо) перпендикулярно данному ненулевому вектору n A ; B .

Возьмем на прямой произвольную точку М(х, у) и рассмотрим вектор

то есть

Уравнение (11) называется уравнением прямой, про-

ходящей через заданную точку перпендикулярно заданному вектору.

Вектор n A ; B , перпендикулярный прямой, называется

нормальным вектором этой прямой.

Уравнение (11) можно переписать в виде

где А и В — координаты нормального вектора,

С = - Ахо - Byо — свободный член. Уравнение (12) есть общее уравнение прямой (см. (7)).

4.2.7. Полярное уравнение прямой

Найдем уравнение прямой в полярных координатах. Ее положение можно определить, указав расстояние р от полюса О до данной прямой и угол а между полярной осью ОР и осью l , проходящей через полюс О перпендикулярно данной прямой (см. рис. 16)

Для любой точки М(г; ) на данной прямой имеем:

пр l OM p .

Полученное уравнение (13) и есть уравнение прямой в полярных координатах.

4.2.8. Нормальное уравнение прямой

Пусть прямая определяется заданием р и (см. рис. 17). Рассмотрим прямоугольную систему координат Оху. Введем полярную систему, взяв О за полюс и Ох за полярную ось. Уравнение прямой можно записать в виде

Множитель называется нормирующим множителем.

Согласно третьему равенству С = - р знак нормирующего множителя противоположен знаку свободного члена С общего уравнения прямой.

Пример. Привести уравнение - 3x + 4y +15=0 к нормальному виду.

Решение: Находим нормирующий множитель

получим искомое нормальное уравнение прямой:

5.Линии второго порядка на плоскости

5.1.Основные понятия

Рассмотрим линии, определяемые уравнениями второй степени относительно текущих координат

крайней мере одно из чисел A, B или C отлично от нуля. Такие линии называются линиями (кривыми) второго порядка. Ниже будкт установлено, что уранение (1) определяет на плоскости окружность, эллипс, гиперболу или параболу.

окружности (см. рис. 18).

Тогда из условия МоМ=R получаем уравнение

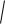(x x0 )2 ( y y0 )2 R ,

то есть

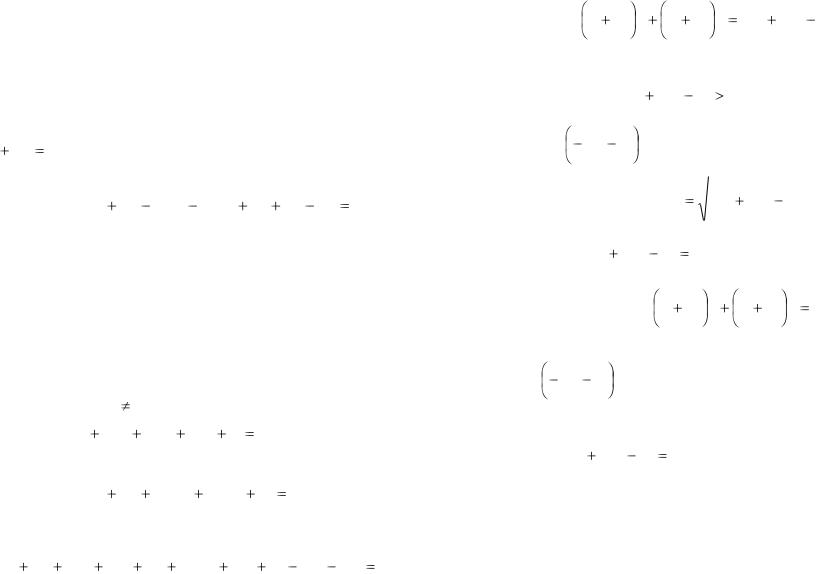
Уравнению (16) удовлетворяют координаты любой точки М(x;y) данной окружности и не удовлетворяют координаты никакой точки, не лежащей на окружности.

Уравнение (16) называется каноническим уравнением

Уравнение окружности (16) после несложных преобразований

сравнении этого уравнения с общим уравнением (16) кривой второго порядка легко заметить, что для уравнения окружности выполнено два условия:

Рассмотрим обратную задачу. Положив в уравнение (16) значение B=0 и A=C 0, получим

т.е.

равносильное уравнение (16), не определяет никакой линии, т.к. первая часть уравнения (17) отрицательна, а левая часть – неотрицательна (говорят: ―окружность мнимая‖).