МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

Федеральное государственное бюджетное образовательное учреждение высшего образования

«Воронежский государственный технический университет»

Кафедра физики

МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ И УПРУГИЕ ВОЛНЫ

МЕТОДИЧЕСКИЕ УКАЗАНИЯ по физике

для студентов всех технических направлений и специальностей очной формы обучения

Воронеж 2022

1

ВВЕДЕНИЕ

Как показывает опыт преподавания, студенты более охотно пользуются методическими разработками по различным темам курса, нежели «большой» учебной литературой. Более сжатое, лаконичное изложение отдельных вопросов предмета оказывается для студента предпочтительнее. Однако компактное изложение материала не должно быть чрезмерно упрощённым и содержать пробросы важных элементов теории. Всё это налагает высокие требования к разработке методических указаний.

Впредлагаемых методических указаниях вопросы механических колебаний и упругих волн изложены предельно кратко, но наряду с этим, сохраняют должный уровень содержания, отвечающий стандартной вузовской программе по общему курсу физики.

Вметодических указаниях представлены примеры решения ряда задач, иллюстрирующие кинематику и динамику колебательных движений.

3

МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ. УПРУГИЕ ВОЛНЫ

1. МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ

1.1. Гармонические колебания

Колебаниями называются движения или процессы, характеризующиеся той или иной степенью повторяемости во времени. В зависимости от физической природы повторяющегося процесса в физике выделяются колебания механические, электромагнитные, а в сложных колебательных системах могут быть те и другие.

Рассмотрим основные вопросы теории механических колебаний. Простейшими по характеру колебаний являются гармонические колебания, при которых колеблющаяся величина изменяется по закону синуса или косинуса. Физическая система, совершающая периодические колебания называется осциллятором (от латинского «oscillo» - качаюсь).

Идеализированные системы, в которых колебания возникают за счет первоначально сообщенной энергии при отсутствии последующих внешних воздействий, называются гармоническими осцилляторами. Примерами гармонических осцилляторов являются пружинный, математический и физический маятники совершающие малые колебания. Колебания, возникающие в таких системах при отсутствии сил трения, называются собственными гармоническими колебаниями.

Рассмотрим кинематику гармонического колебания. Смещение системы от положения равновесия определяется формулой

где x - смещение материальной точки в произвольный момент времени от своего положения равновесия, A - амплитуда колебаний, т.е. максимальное отклонение от положения равновесия;

ϕ = ω0 t +ϕо - фаза колебаний; ϕо - начальная фаза.

4

Периодом колебаний Т называется время одного полного колебания, или время, за которое фаза колебаний получает при-

ращение, равное 2π. Определим его из следующего условия: ω0(t

+ T) + α = ω0t + α + 2π, откуда T = 2π /ω .

Число колебаний в единицу времени называется частотой колебаний и обозначается буквой ν. Частота и период колебаний

– взаимно обратные величины, т.е. ν = 1/T . За единицу частоты принимается частота такого колебания, период которого равен 1 сек. Эту единицу называют герцем (Гц). Таким образом, эти величины связаны соотношениями

Величину ω называют круговой или циклической, т.е. ω дает число колебаний за 2π секунд.

Уравнение (5) называется дифференциальным уравнением гармонических колебаний. Общее решение этого уравнения имеет вид (1).

На рис.1 представлены зависимости смещения, скорости и ускорения для гармонических колебаний.

Простейшим примером системы, совершающей гармонические колебания, является пружинный маятник - материальная точка массой m на невесомой пружине с коэффициентом жесткости k.

5

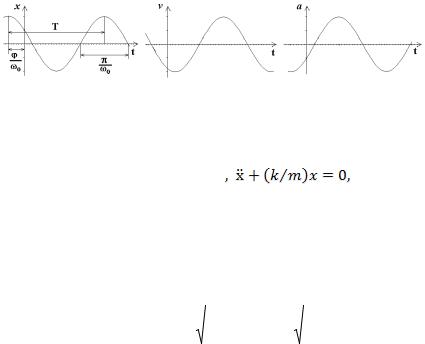
Рис.1 Выведем маятник из положения равновесия и предоставим

систему самой себе. По II закону Ньютона ma = F , где сила определяется законом Гука. Тогда

где m - масса материальной точки, k - коэффициент жесткости

пружины. Обозначив ω02 = k/m, получаем дифференциальное уравнение гармонических колебаний (5), общее решение кото-

рого определяется формулой (1), а ω0 определяет циклическую частоту собственных колебаний пружинного маятника. Таким образом, для пружинного маятника

1.2. Энергия гармонического колебания

Используя выражение скорости (3), определим кинетическую энергию гармонического осциллятора

Потенциальная энергия выражается формулой:

Складывая (8) и (9) с учетом (7), получим полную энергию колебания:

6

Таким образом, полная энергия гармонического колебания является величиной постоянной. Этого и следовало ожидать, так как квазиупругая сила является консервативной.

1.3.Маятники

Маятник – это твердое тело, совершающее под действием силы тяжести колебания вокруг неподвижной точки или оси. Наиболее известными являются математический и физический маятники.

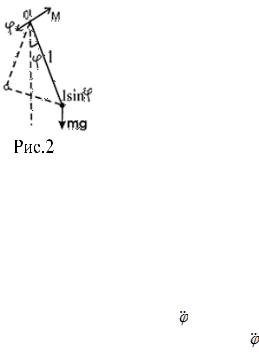
Математическим маятником называют идеализированную систему, состоящую из невесомой и нерастяжимой нити, на которой под-

вешена масса, сосредоточенная в одной точке (рис.2.).

При отклонении маятника от положения равновесия на

угол ϕ возникает вращательный момент М = - mgl sinϕ (m – масса маятника, l – длина маятника).

Поэтому так же, как смещению и квазиупругой силе, мо-

менту М и угловому смещению ϕ нужно приписывать противоположные знаки. По основному закону динамики вращательно-

где ml2 – момент инерции маятника, - угловое ускорение. Ог-

раничимся рассмотрением малых колебаний. В этом случае можно положить sinϕ ≈ ϕ. Введя обозначение g/l =ω02, получаем дифференциальное уравнение гармонических колебаний ϕ

+ω02ϕ = 0, общее решение которого имеет вид

ϕ = A cos(ω0t+ϕо), где А и ϕо - постоянные, определяемые начальными условиями возбуждения колебаний.

7

Таким образом, при малых колебаниях математический маятник колеблется по гармоническому закону. Период колебаний математического маятника

Физический маятник – твердое тело,

совершающее под действием силы тяжести колебания вокруг горизонтальной неподвижной оси, не проходящей через центр тяжести тела. При отклонении маятника от по-

ложения равновесия на некоторый угол ϕ возникает момент силы тяжести, стремящийся вернуть маятник в положение равновесия.

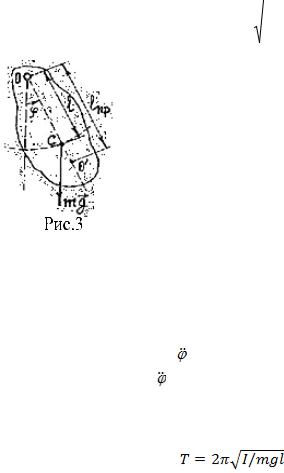
Этот момент равен M = - mgl sinϕ, где

m - масса маятника, а l – расстояние от центра тяжести С тела до оси вращения О (рис.3.). Знак « - » имеет тоже значение, что и в случае формулы (11). Обозначив момент инерции маятника относительно оси О буквой I, можно написать дифференциаль-

а период колебаний физического маятника определяется выражением

будет иметь такой же период колебаний, как и данный физический маятник.

8

Величину (17) называют приведенной длиной физического маятника. Таким образом, приведенная длина физического маятника – это длина такого математического маятника, период колебаний которого совпадает с периодом данного физического маятника.

Точка на прямой, соединяющей точку подвеса с центром инерции, расположенная на расстоянии приведенной длины от оси вращения, называется центром качания физического маятника. (см. т. О’ на рис. 3). Точка подвеса и центр качания являются взаимозаменяемыми, т.е. если маятник подвесить за центр качания О’, то его период не изменится и прежняя точка О станет новым центром качания.

1.4. Сложение колебаний одного направления

Для графического представления гармонических колебаний используется метод вращающегося вектора амплитуды или метод векторных диаграмм (рис.4).

Введем ось Х и из точки О, взятой на этой оси, отложим ве ктор длины А, образующий с осью угол α. Если привести вектор А во

(ω0t+ϕо). Следовательно, гармоническое колебание может быть задано с помощью вектора амплитуды.

9