1. РЕШЕНИЕ ТИПОВОГО ВАРИАНТА КОНТРОЛЬНОЙ РАБОТЫ

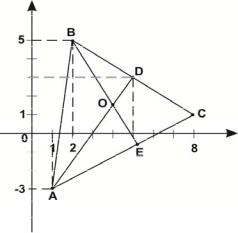
Задача 1. Даны вершины треугольника: А (1,-3), В (2,5) и С (8,1). Найти точку пересечения медианы, проведенной из вершины А и высоты – из вершины В, а также длину медианы, проведенной из вершины А.

Решение:

Рис. 1

Составим уравнение медианы АD. Координаты точки D

3). Используем уравнение прямой, проходящей через две

Уравнение медианы AD: 3x 2y 9 0 .

Составим уравнение высоты, проведенной из вершины В. Так

Используем уравнение прямой, проходящей через данную точку М0 (x0,y0) в данном направлении y y0 k(x x0 ) .

7x 4y 34 0 .

Для нахождения координат точки пересечения медианы, проведенной из вершины А и высоты, проведенной из вершины В нужно решить совместно из уравнения

Длина медианы определяется по формуле расстояния d между точками А (x1,y1)и D (x2,y2) на плоскости

d 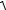(x2 x1)2 ( y2 y1)2 .

А (1,-3), D (5,3) d AD 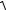(5 1)2 (3 3)2 16 36 2 13 .

Задача 2. Составить уравнения прямых, проходящих через начало координат и образующих с прямой

3x y 5 0 угол 4 .

Решение: Уравнения искомых прямых имеют вид y kx , так

как прямые проходят через начало координат. Задача имеет два решения (Рис. 2). Для решения используем формулу

угол, правую часть формулы возьмём по абсолютной величине. Пусть угловой коэффициент одной из искомых прямых равен k. Угловой коэффициент заданной прямой равен

2

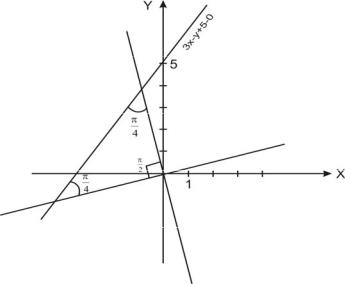
3. Так как угол между этими прямыми равен 4 , то

Решая каждое из получившихся уравнений, находим, что

Задача 3. Даны вершины А (-3,-2), В (4,-1), С (1,3) трапеции

ABCD (AD BC). Составить уравнение средней линии трапеции. Полученное уравнение привести к уравнению в «отрезках» и к нормальному.

3

Решение: Составим уравнение прямой ВС (уравнение прямой, проходящей через две точки).

От общего уравнения прямой ( Ax By C 0 ) перейдем к уравнению с угловым коэффициентом ( y kx b ).

y 43 x 133 , где kBC 43

Средняя линия трапеции параллельна ВС и проходит через

уравнение прямой

y y0 k(x x0 )

y 32 43 (x 12)

Уравнение средней линии трапеции: 8x 6y 5 0 . Уравнение прямой в отрезках:

4

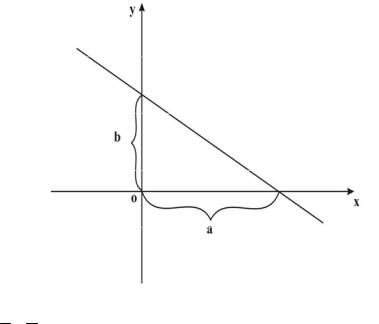
Рис. 3

ax by 1, а – величина отрезка отсекаемого прямой на оси

ОХ, b - величина отрезка отсекаемого прямой на оси ОY. Перенося свободный член данного уравнения в правую часть равенства, получим 8x 6y 5 . Деля обе части равенства на

5

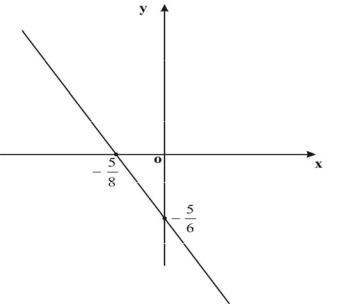
Рис. 4

Нормальное уравнение прямой (Рис. 5) x cos y sin p 0 , р – длина перпендикуляра, опущенного из начала координат на

прямую, - угол, который образует этот перпендикуляр с положительным направлением оси ОХ.

6

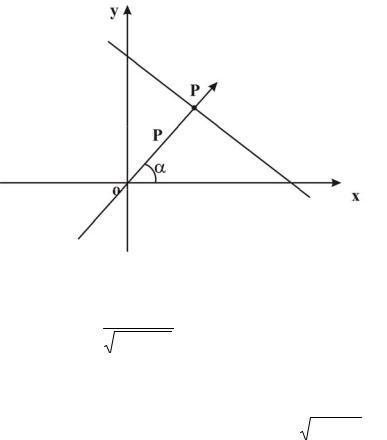
Рис. 5 Для приведения общего уравнения прямой к нормальному

виду обе его части надо умножить на нормирующий

выбрать знак, противоположный знаку свободного члена С в общем уравнении прямой.

(знак минус берется потому, что С = 5 0). Таким образом,

перпендикуляра из начала координат к прямой p 12 .

7

Задача 4. Найти расстояние между параллельными прямыми

3x 4y 15 0 и 3x 4y 20 0 .

Решение: Искомое расстояние найдем как расстояние от произвольной точки первой прямой до второй прямой. Возьмем на первой прямой произвольную точку, например, точку с абсциссой x 1. Её ордината y 3 . Итак, на первой

прямой выбрана точка А (1;3). Найдем теперь расстояние этой

Задача 5. Даны точки М1 (-3; 7; -5) и М2 (-8; 3; -4). Составить уравнение плоскости, проходящей через точку М1 и

2x 4y 5z 21 0, x 3z 18 0, 6x y z 30 0 провести плоскость, параллельную плоскости 3x y 5z 6 0 . Найти

расстояние точки М1 (1; -1; -1) до построенной плоскости. Решение: Плоскости пересекаются, следовательно

8