
Учебное пособие 559
.pdf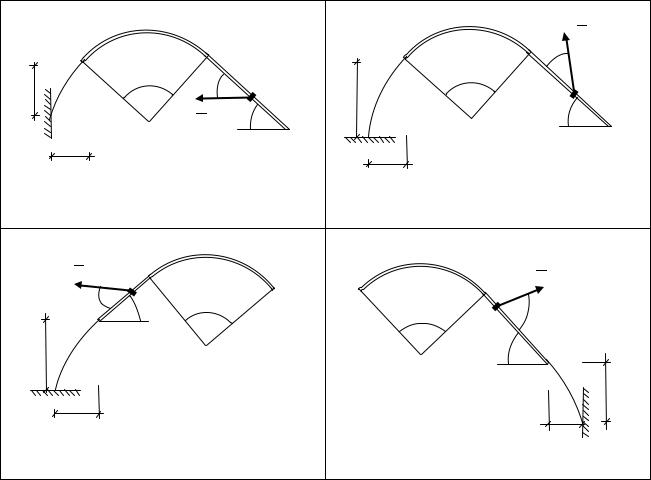
|
|
|
B |
|
|
|
B |
F |
|
|
|
|
|
|
γ |
||
|
C |
|
γ |
|
C |
|
|
|
b |
|
|
α |
|
|
|||
|
α |
|
b |
|
|
|||
|
F |
β |
|
β |
||||
|
|
O |
|
O |
|
|||
|
a |
|
A |
a |
|
A |
||
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
Рис. 6 |
|
|
|
Рис. 7 |
|
|
|
F |
B |
|
A |
A |
B |
F |
|
|
γ |
|
|
|
||||
|
β |
|
|
|
||||
|
C |
α |
|
|
γ |
|
|
|
|
|
|
α |
|
|
|
||
b |
|
O |
|
β |
|
C |
||
|
|
|
O |
|
||||
|
|
|
|
|
|
|
b |
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 8 |
|
|
|
Рис. 9 |
|
|
|
|
|
Исходные данные к задаче Д1 |
|
|
Таблица 1.2 |
||
|
|
|
|
|
|
|||
Последняя |
F |
R |
v0 |
α |
β |
γ |
m |
t1 |
а |
цифра |
Н |
Н |
м/с |
град |
град |
град |
кг |
c |
м |
шифра |
|||||||||
0 |
2cos(πt /5) +t |
5 |
15 |
60 |
45 |
60 |
0.5 |
4 |
5 |
|
|
|
|
|
|
|
|
|
|
1 |
0.2exp(t / 4) + 4 |
9 |
10 |
75 |
60 |
75 |
0.2 |
3 |
2 |
|
|
|
|
|
|
|
|
|
|
2 |
2cos(πt / 4) +3t2 |
13 |
12 |
45 |
30 |
45 |
0.9 |
2 |
7 |
3 |
0.4exp(t / 2) + 4 |
14 |
16 |
30 |
15 |
30 |
0.4 |
5 |
6 |
|
|
|
|
|
|
|
|
|
|
4 |
4sin(πt / 2) +5t |
10 |
14 |
90 |
75 |
15 |
0.3 |
3 |
9 |
|
|
|
|
|
|
|
|
|
|
5 |
0.4exp(t / 5) + 4t |
7 |
11 |
60 |
30 |
60 |
0.6 |
4 |
8 |
|
|
|
|
|
|
|
|
|
|
6 |
3sin(πt / 6) +t3 |
11 |
17 |
45 |
15 |
30 |
0.8 |
3 |
4 |
7 |
4cos(πt /3) +3t |
8 |
20 |
75 |
45 |
45 |
0.5 |
5 |
10 |
|
|
|
|
|
|
|
|
|
|
8 |
2sin(πt / 4) +t 2 |
6 |
14 |
60 |
45 |
15 |
0.4 |
3 |
6 |
9 |
0.4exp(t / 2) +t |
15 |
13 |
90 |
60 |
75 |
0.3 |
6 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
11 |
|
|
|
|
|
|

ЗАДАЧА Д2
Груз массой m закреплён с помощью двух пружин. Начало координат находится в положении статического равновесия груза. Выведенный из этого состояния, груз движется вдоль оси Ох под действием силы тяжести G , силы упругости пружины F и силы сопротивления движению R = −µv . Найти
уравнение, частоту k*, период Т* и логарифмический декремент bT* затухающих колебаний, а также уравнение, амплитуду А, циклическую (круговую) частоту k, период Т и частоту ν свободных колебаний груза.
Варианты крепления груза показаны на рис. 0 – 9 таблицы 2.1, числовые значения даны в таблице 2.2. Здесь m – масса груза, μ – коэффициент вязкости, с – жёсткость пружины, x0 и v0 – начальные положение и скорость груза соответственно (знак при x0 и v0 показывает, в какую сторону от положения равновесия смещён груз и куда направлена скорость: минус – в сторону отрицательных значений х, плюс – в сторону положительных).
Указания. Задача Д2 относится к теме прямолинейных колебаний точки [1, §§94, 95], [2, §§11, 14]. При решении необходимо составить дифференциальное уравнение прямолинейного движения груза, принимаемого за материальную точку, а затем проинтегрировать это уравнение. Так как в общем случае груз закреплён с помощью двух пружин различной жёсткости, то предварительно определяется приведённая жёсткость сп этих пружин. В случае параллельного соединения пружин (рис. 1, 3, 4, 6, 8)
сп =с1 + с2 ;
в случае их последовательного соединения (рис. 0, 2, 5, 7, 9)
сп =с1с2 /(с1 + с2 ) ,
где с1, с2 – жёсткости пружин [1, §94, задачи 113, 114; 2, §13, пример 3]. Затухающие колебания точки описываются уравнением вида [1, §95], [2,
§14]
x + 2bx + k 2 x =0 , где 2b = µ/ m, k 2 =cп / m .
Это дифференциальное уравнение является линейным однородным уравнением второго порядка. Его решение ищется как линейная комбинация функций вида x=ent. Подставляя x, x, x в дифференциальное уравнение, получим
характеристическое уравнение
n2 + 2bn + k 2 =0,
корни которого будут
n1,2 = −b ± 
 b2 − k 2 .
b2 − k 2 .
Возможны три случая:
а) k>b (сопротивление мало). Тогда решение записывается в виде
|
|
x =e−bt (C cosk*t +C |
2 |
sin k*t) , |
||
|
|
1 |
|
|
|
|
где k* = k 2 −b2 . Либо, положив C = Asinα , C |
2 |
= Acosα , получим |
||||
1 |
|
|
|
|||
12 |
|
|
|
|
||

x = Ae−bt sin(k*t +α) .
Постоянные интегрирования С1, С2 |
или |
А, α |
|
определяются по начальным |
|||||||
условиям задачи x(0) = x0 , |
x(0) =v0 . При этом |
|
|
|
|
|
|||||
A2 = x02 + |
(v |
|
+bx |
|
)2 |
tgα = |
x |
0 |
k 2 −b2 |
|
|
|
0 |
|
0 |
, |
|
|
. |
||||
k 2 −b2 |
|
v0 |
|
||||||||
|
|
|
|
+bx0 |
|||||||
График колебаний в этом случае имеет вид кривой на рис. 2.1.
Рис. 2.1. График затухающих колебаний точки
б) k=b. Корни характеристического уравнения являются равными n1=n2=-b, и общее решение принимает вид
x =e−bt (C +C |
t) . |
|
1 |
2 |
|
С1 и С2 определяются из условий x(0) = x0 , |
|
x(0) =v0 : |
|
C1 = x0 , |
|
C2 =v0 +bx0 . |
||||||
в) k<b. Общее решение имеет вид |
|
|
|
|
|||||
|
|
x =C en1t +C |
en2t , |
||||||
|
1 |
|
|
2 |
|
|
|
|
|
где n1 и n2 являются отрицательными числами. |
|||||||||
|
v = x = n C en1t + n |
C |
en2t . |
||||||
|
1 |
1 |
|
2 |
2 |
|
|
||
Постоянные интегрирования определяются по начальным условиям: |
|||||||||
x(0) = x0 =C1 +C2 , |
|
x |
(0) =v0 = n1C1 + n2C2 . |
||||||
Решая полученную систему двух алгебраических уравнений, найдём |
|||||||||
C = v0 − n2 x0 |
, |
C = v0 − n1x0 . |
|||||||
1 |
|
n1 − n2 |
|
|
1 |
|
n2 − n1 |
|
|
|
|
|
|
|
|
||||
В случаях б) и в) движение колебательным не будет, и точка со временем асимптотически стремится к равновесному положению х=0 (рис. 2.2).
13
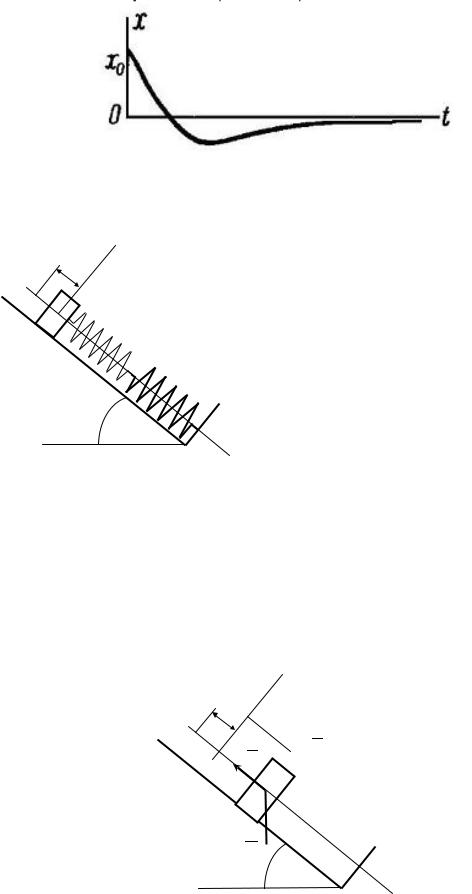
Рис. 2.2. График апериодического движения точки
Пример Д2.
y
λст |
|
|
|
|
|
|
|
|
Дано: m=6 кг, μ=48 Н·с/м, с=900 Н/м, |
||||
с/2 |
|
|
x0=0.1 м, v0= –5 м/с, с1=с/2, с2=с. |
|||
|
с |
Найти: |
уравнение затухающих |
|||
|
|
* |
* |
* |
; |
|
|
|
|
колебаний, k |
, T |
, bT |
|
|
|
|
уравнение свободных колебаний, |
|||
45 |
|
x |
А, k, T, ν. |
|
|
|
|
|
|
|
|
|
|
Рис. 2.3. Условие задачи
Решение. Предварительно определим приведённую жёсткость пружинного крепления, состоящего из двух последовательно соединённых пружин. В этом случае
с |
п |
= |
с1с2 |
|
= |
с с/ 2 |
= |
с |
=300 |
(Н/м). |
|
с + с |
2 |
с + с/ 2 |
3 |
||||||||
|
|
|
|
|
|
||||||
|
|
|
1 |
|
|
|
|
|
|
Груз изобразим в смещённом положении, скорость направлена в положительном направлении оси Ох (рис. 2.4).
y
λст
x
0 F 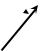 N
N
G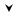
45 x
Рис. 2.4. Силы, действующие на груз
14

Так как наличие постоянной силы тяжести G не изменяет характера колебаний, а лишь смещает центр колебаний в сторону действия этой силы на величину статического отклонения λст, то дифференциальное уравнение движения точки будет
mx = Fx + Rx = −cx − µx .
Разделив обе части равенства на m, получим |
|
|
|
|
|
|
||||||
x + 2bx + k 2 x =0 , где 2b = µ/ m, |
|
|
k 2 =cп / m . |
|||||||||
В соответствии с исходными данными рассматриваемой задачи |
||||||||||||
|
|
|
b = µ/ 2m = 4 с-1, |
k = cп / m =7.07 с-1. |
||||||||
Так как k>b, то решение ищется в виде (см. указания к задаче) |
||||||||||||
x = Ae−bt sin(k*t +α) , где b = 4 с-1, k* = |
|
|
|
|
|
= 5.83 с-1; |
||||||
|
|
k 2 −b2 |
||||||||||
A |
2 |
2 |
|
(−5 + 4 0.1)2 |
|
A |
|
=0.795 м; |
||||
|
|
|||||||||||
|
=0.1 + |
50 −16 |
=0.632, |
|
|
|||||||
tgα = 0.1 |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
||||||||
|
50 −16 |
= −0.127 , |
α = arctg(−0.127) = −0.126 рад. |
|||||||||
−5 + 4 0.1 |
|
|
|
|
|
|
|
|
||||
Знак постоянной А выбирается так, чтобы были удовлетворены начальные условия задачи. В данном примере необходимо положить А = – 0.795 м. Действительно, решение
x = −0.795e−4t sin(5.83t −0.126)
удовлетворяет условиям x(0) = x0 =0.1 м, x(0) =v0 = −5 м/с: x(0) = −0.795sin(−0.126) =0.0999 ≈0.1 м;
x = −0.795[−4e−4t sin(5.83t −0.126) + e−4t 5.83cos(5.83t −0.126)]; x(0) = −0.795[−4sin(−0.126) +5.83cos(−0.126)] = −4.998 ≈ −5 м/с.
|
|
|
|
|
|
|
|
Частота |
затухающих колебаний |
k* = k 2 −b2 , |
период T * = 2π / k* , |
||||
логарифмический декремент bT*: |
|
|
|
|
|
|
|
k* = |
50 −16 =5.83 с-1, T * = 2π / |
|
|
=1.078 с, |
bT* = 4.312. |
||
|
34 |
||||||
Для свободных колебаний точки решения легко получить из представленных выше соотношений затухающих колебаний, положив в них коэффициент μ, а, следовательно, и b равными нулю. При этом дифференциальное уравнение свободных колебаний точки принимает вид
x + k 2 x =0, где k 2 =cп / m .
Его решение в общем виде соответственно
x = Asin(kt +α),
где константы А и α определяются равенствами
A2 = x02 + |
v0 2 |
, |
tgα = |
kx0 |
. |
k 2 |
|
||||
|
|
|
v0 |
||
В соответствии с данными рассматриваемой задачи k 2 =300/ 6 =50, k = 
 50 ≈7.07 с-1;
50 ≈7.07 с-1;
15

A2 =0.01 + 25/50 =0.51, A ≈0.714 м;
tgα = −0.1
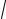 50 /5 ≈ −0.141, α = arctg(−0.141) = −0.14 рад.
50 /5 ≈ −0.141, α = arctg(−0.141) = −0.14 рад.
Чтобы удовлетворить начальным условиям задачи, необходимо положить
А= – 0.714. Тогда уравнение свободных колебаний точки
x= −0.714sin(7.07t −0.14) .
Модуль А определяет амплитуду свободных колебаний |A| = 0.714 м; циклическая частота k =7.07 с-1; период колебаний T = 2π / k = 2π / 
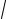 50 =0.889 с;
50 =0.889 с;
частота колебаний ν =1/T = k / 2π = 
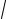 50 / 2π =1.125 с-1.
50 / 2π =1.125 с-1.
Можно отметить, что амплитуда и период свободных колебаний точки при одних и тех же исходных данных несколько меньше амплитуды и периода её затухающих колебаний.
Таблица 2.1 Варианты рисунков к задаче Д2 (предпоследняя цифра шифра)
с/2 |
с |
|
с |
||
с |
|
|
x |
x |
|
30 |
||
|
Рис. 0 |
Рис. 1 |
с |
|
с/4 |
с |
с/3 |
x |
|
 x
x
Рис. 2 |
Рис. 3 |
16
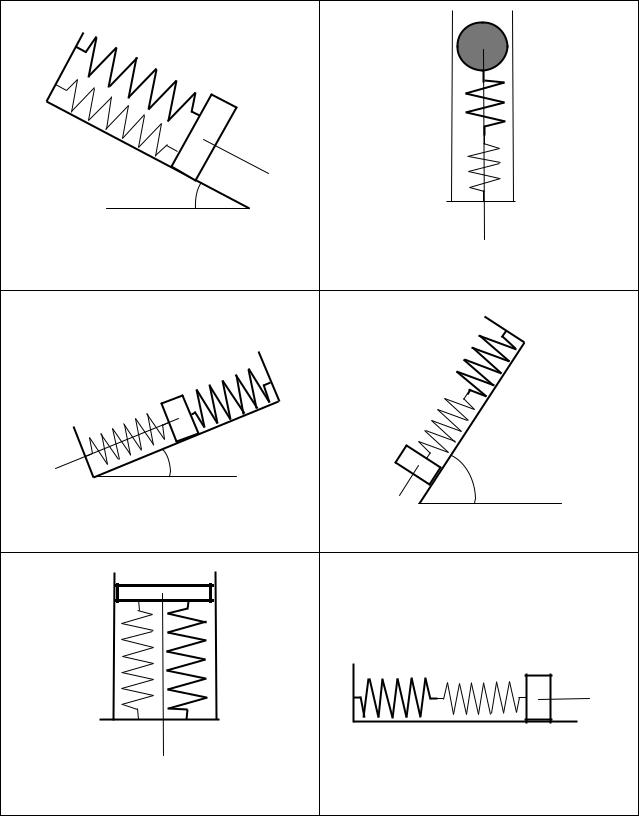
5с/4 |
|
|
2с |
с |
x |
|
3с/2 |
45 |
|
|
x |
Рис. 4 |
Рис. 5 |
|
2с |
3с/2 |
|
|
|
|
с/2 |
с |
x |
30 |
|
|
x |
60 |
|
Рис. 6 |
Рис. 7 |
3с/4 |
с |
2с |
с |
|
|||
|
|
|
x |
x |
|
Рис. 8 |
Рис. 9 |
17
|
|
Исходные данные к решению задачи Д2 |
Таблица 2.2 |
|||
|
|
|
||||
|
|
|
|
|
|
|
Посл. цифра |
m |
|
μ |
с |
x0 |
v0 |
шифра |
кг |
|
Н·с/м |
Н/м |
м |
м/с |
0 |
12 |
|
50 |
250 |
–0.4 |
0 |
1 |
20 |
|
150 |
1500 |
0 |
– 6 |
2 |
7 |
|
10 |
50 |
0.2 |
3 |
3 |
30 |
|
100 |
1000 |
0.12 |
0 |
4 |
10 |
|
20 |
400 |
– 0.05 |
– 1 |
5 |
18 |
|
120 |
1000 |
0 |
3 |
6 |
8 |
|
20 |
500 |
– 0.15 |
0 |
7 |
25 |
|
200 |
2000 |
0.07 |
2 |
8 |
5 |
|
48 |
1200 |
0 |
– 2 |
9 |
15 |
|
80 |
1000 |
0.3 |
4 |
ЗАДАЧА Д3
Механизм, состоящий из груза А, блока В (больший радиус R, меньший r, радиус инерции i) и цилиндра С, установлен на призме D, находящейся на горизонтальной плоскости. Блок В (рис. 0, 1, 3, 4, 5, 7) или цилиндр С (рис. 2, 6, 8, 9) прикреплён к призме на оси.
Задание 1. Призма не закреплена, трение между призмой и плоскостью отсутствует. Груз А получает перемещение s по вертикали вниз (рис. 0 – 2) или вдоль поверхности призмы вправо (рис. 3, 4), по наклонной плоскости (рис. 5 – 9). Куда и на какое расстояние переместится призма?
Задание 2. Призма закреплена на плоскости. Механизм из состояния покоя под действием сил тяжести пришёл в движение. Груз А движется по шероховатой поверхности с коэффициентом трения f (кроме рис. 0 – 2), качение цилиндра (блока) происходит без проскальзывания, коэффициент трения качения равен k.
Какую скорость и ускорение приобретёт груз А, пройдя расстояние s? Ускорение определить двумя способами, используя соотношения теоремы об изменении кинетической энергии системы, и с помощью общего уравнения динамики.
Указания. В задаче Д3 рассматривается динамика механической системы. В задании 1 необходимо применить теорему о движении центра масс системы [1, §107], [2, §43]. В задании 2 при определении скорости груза и его ускорения первым способом используется теорема об изменении кинетической энергии системы [1, §§121, 123], [2, §§67-69], а при определении ускорения вторым способом необходимо составить общее уравнение динамики [1, §141], [2, §117].
18
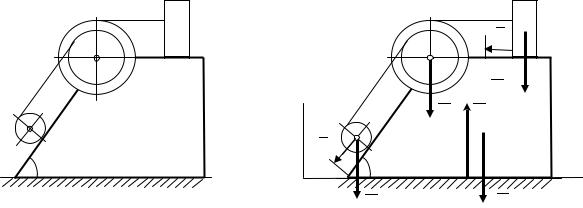
Пример Д3.
Дано: mA = 50 кг, mB = 80 кг, mC = 120 кг, mD = 210 кг, R/r = 3, i/r = 1.5, k/r = 0.2, f = 0.1, α = 75o, s = 1.2 м (рис. 3.1).
Найти: 1) D; 2) vA, a.
|
|
B |
|
|
B |
A |
|
|
A |
|
|
|
S |
|
|
|
|
|
|
|
C |
|
D |
y |
|
|
GA |
|
C |
GB |
N |
|||
|
|
|
|
|||
|
|
R C = r/2 |
|
SC |
|
D |
|
α |
|
α |
x |
||
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
GC |
GD |
Рис. 3.1. Условие задачи |
Рис. 3.2. Внешние силы системы |
|||||
|
|
|
|
|
тел А, В, С и D |
|
Решение. Задание 1: призма не закреплена, найти смещение D. Изобразим систему в произвольном положении, приложив все
действующие на неё внешние силы – силы тяжестей тел и нормальную реакцию плоскости (рис. 3.2). Так как проекции этих сил на горизонтальную ось Ох равны нулю, то по теореме о движении центра масс
Mxц = ∑Fkxe =0, xц =0, xц =const =0,
так как в начальный момент скорости тел системы равны нулю (хц – координата центра масс системы в проекции на ось Ох). Следовательно
xц =const.
Если обозначить xA, xB, xC, xD координаты центров масс соответствующих тел системы до перемещения грузов А и С, а A, B, C, D изменения координат центров масс этих тел после смещения груза, то по известной формуле для координаты центра тяжести системы будем иметь
|
xц = |
mA xA + mB xB + mC xC + mD xD |
|
(до смещения); |
|
||
mA + mB + mC + mD |
|
||||||
|
|
|
|
|
|
||
xц = |
mA (xA + ∆A ) + mB (xB + ∆B ) + mC (xC + ∆C ) + mD (xD + ∆D ) |
|
(после). |
||||
|
|||||||
|
|
mA + mB + mC + mD |
|
|
|
|
|
Вычитая из второго равенства первое, получим |
|
|
|
|
|||
|
|
mA∆A + mB ∆B + mC ∆C + mD ∆D =0. |
|
|
|
||
Выразим абсолютные смещения A, B, |
C через s. |
Центры масс тел |
|||||
совершают сложное движение. Абсолютные |
смещения |
тел |
А, В, С |
||||
(относительно неподвижной опорной плоскости) состоят из сумм смещений относительно призмы и переносного смещения D. Направление оси Ох
19

определяет знаки смещений: вправо с плюсом, влево с минусом. Предположим, что призма смещается в сторону, противоположную направлению смещения тел А и С, то есть вправо. Перемещение центра цилиндра С относительно призмы и перемещение груза А связаны между собой также, как связаны их скорости. Из кинематики
ω |
B |
= vA , |
ω |
C |
= |
|
ωB r |
, |
v |
|
=ω |
|
R = |
1 |
r |
v |
|
, |
s |
|
= |
1 r |
s . |
||
2R |
|
|
|
|
|
|
|||||||||||||||||||
|
R |
|
|
|
|
|
C |
|
C |
C |
2 R |
A |
|
|
C |
|
2 R |
|
|||||||
Тогда |
|
|
|
|
|
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∆C = −1 |
r |
|
|
|
|
|
|
|
|
|||||
|
|
∆A = −s + ∆D , |
|
∆B = ∆D , |
scosα + ∆D ; |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 R |
|
|
|
|
|
|
|
|
|||
mA (−s + ∆D ) + mB ∆D + mC (−12 Rr scosα + ∆D ) + mD∆D =0.
Отсюда определяем перемещение призмы
∆D = |
mA + mC (r / 2R)cosα |
s = |
50 +120 (1/ 2 3) 0.259 |
1.2 =0.144 (м). |
|
50 +80 +120 + 210 |
|||
|
mA + mB + mC + mD |
|
||
Итак, призма переместится вправо на 0.144 м.
Задание 2: призма закреплена, найти скорость и ускорение груза А.
Для нахождения скорости груза А применим теорему об изменении кинетической энергии системы
T −T0 = ∑Ake +∑Aki .
Для рассматриваемой системы, состоящей из твёрдых тел, соединённых нерастяжимыми нитями, работа внутренних сил равна нулю: ∑Aki =0 . Так как
в начальном положении всё находилось в покое, то начальная кинетическая энергия системы Т0 = 0. Конечная кинетическая энергия Т, которую получила система после того, как груз А переместился на расстояние s, состоит из трёх слагаемых
T =TA +TB +TC .
Груз А совершает поступательное движение, следовательно, его кинетическая энергия равна (v = vA – искомая скорость)
TA = m2A v2.
Блок В вращается относительно неподвижной оси. В этом случае кинетическая энергия
J ω2
TB = B2 B ,
где осевой момент инерции блока вычисляется через радиус инерции JB =i2mB .
Линейная скорость внешнего обода блока совпадает со скоростью груза v, так как обод связан нерастяжимой нитью с грузом. При этом угловая скорость блока определяется формулой кинематики ωB =v / R . Тогда
20
