
Операционное исчисление. методические указания для организации самостоятельной работы по дисциплине «Высшая математика». Пантелеев И.Н
.pdf
Министерство науки и высшего образования Российской Федерации
Федеральное государственное бюджетное образовательное учреждение высшего образования
«Воронежский государственный технический университет»
Кафедра высшей математики и физико-математического моделирования
117-2018
ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
для организации самостоятельной работы по дисциплине «Высшая математика» для студентов направления
20.03.01 «Техносферная безопасность» (профили «Защита в чрезвычайных ситуациях», «Безопасность жизнедеятельности в техносфере», «Защита окружающей среды»)
очной формы обучения
Воронеж 2018
УДК 517.44(07) ББК 22.1я7
Составитель канд. физ.-мат. наук И. Н. Пантелеев
Операционное исчисление: методические указания для
организации |
самостоятельной |
работы |
по |
дисциплине |
«Высшая математика» для студентов направления20.03.01 |
||||
«Техносферная |
безопасность» |
(профили |
«Защита |
в |
чрезвычайных ситуациях», «Безопасность жизнедеятельности в техносфере», «Защита окружающей среды») очной формы обучения / ФГБОУ ВО «Воронежский государственный технический университет»; сост. И. Н. Пантелеев. Воронеж:
Изд-во ВГТУ, 2018. 47 с.
В методических указаниях приведен теоретический материал, необходимый для выполнения заданий и решения типовых примеров.
Предназначены в качестве руководства для организации
самостоятельной |
работы |
по |
дисциплине«Высшая |
математика» по |
разделу «Операционное |
исчисление» для |
|
студентов направления 20.03.01 «Техносферная безопасность» в |
|||
3 семестре. |
|
|
|
Методические указания |
подготовлены в электронном |
||
виде и содержатся в файле Vmfmm_OperIs _18.pdf. Ил. 6. Библиогр.: 8 назв.
УДК 517.44(07) ББК 22.1я7
Рецензент − Г. Е. Шунин, канд. физ.-мат. наук, проф. кафедры высшей математики и физико-математического
моделирования ВГТУ
Издается по решению учебно-методического совета Воронежского государственного технического университета
1. Оригинал и изображение
Оригиналом называется функция f (t) , определенная на всей числовой осиt и удовлетворяющая следующим условиям:
1.f (t) непрерывна во всей области определения, за
исключением, может быть, конечного числа точек разрываI рода на каждом отрезке конечной длины;
2. |
|
|
f (t) = 0 при t < 0 ; |
|
|
|
|
|
|
|
|
|
|||||
3. |
|
|
f (t) |
при t |
® ¥ |
|
возрастает |
не |
быстрее |
|
некоторой |
||||||
экспоненциальной функции, то есть существуют такие числа |
|||||||||||||||||
M > 0, s0 |
³ 0 , что для всякого t ³ 0 выполняется неравенство |
||||||||||||||||
|
f (t) |
|
|
< Mes0t , |
где |
наименьшее |
из |
чиселs |
|
, при |
котором |
||||||
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
выполняется |
неравенство, называется |
показателем |
|
роста |
|||||||||||||
оригинала. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
Замечание. В дальнейшем для краткости записи будем |
|||||||||||||
писать y = f (t) . Под этим будем понимать следующее: |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
y = |
ì f (t), если |
t ³ 0; |
|
|
|
|
|||
|
|
|
|
|
|
|
|
í |
0, если t < 0. |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
î |
|
|
|
|
|
|||
|
|
|
|
Изображением |
функции |
f (t) называется |
|
функция |
|||||||||
|
F ( p) |
|
комплексного |
|
переменногоp = s + is , которая |
||||||||||||
определяется равенством |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
¥ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F ( p) = ò f (t)e- pt dt. |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
Интеграл |
называется интегралом Лапласа функции |
||||||||||||
|
f (t) . |
Операция |
перехода |
от |
оригинала f (t) |
|
к изображению |
||||||||||
|
F ( p) |
|
называется |
|
преобразованием |
|
Лапласа. Теория |
||||||||||
преобразования |
|
Лапласа |
называется |
|
операционны |
||||||||||||
исчислением. |
Тот |
факт, что |
f (t) |
и F ( p) относятся |
|
друг к |
|||||||||||
другу |
|
как |
|
оригинал |
|
и |
изображение, записывают |
так: |
|||||||||
|
f (t) Û F ( p) |
или L[ f (t)] = F ( p); F ( p) Û f (t). |
|
|
|||||||||||||
3
Можно доказать, что при выполнении условий 1–3 для
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¥ |
|
|
|
|
|
|
|
|
функции f (t) |
несобственный интеграл ò f (t)e- pt dt |
сходится |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
абсолютно и равномерно при Re p = s > s0 . |
|
|
|
|
|
|
|
||||||||||||||||||
2. Единичная функция Хевисайда и ее изображение |
|||||||||||||||||||||||||
Единичной |
функцией |
Хевисайда называется |
|
функция |
|||||||||||||||||||||
вида |
|
|
|
|
|
|
|
ì1, при t ³ 0, |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
h |
(t) = |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
í |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
î0, при t < 0. |
|
|
|
|
|
|
|
|
|
||||||||
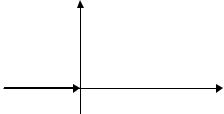
График функции (рис.1) имеет вид |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
h(t) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
Рис. 1 |
|
|
|
|
t |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Любой |
|
|
|
|
|
|
|
|
|
ì f (t), при t ³ 0, |
|
|
|
|
помощи |
||||||||||
|
оригинал y = í |
|
|
|
|
|
при |
|
|
|
|
||||||||||||||
|
|
|
функции h(t) |
|
|
|
|
î 0, при t < 0 |
|
|
|
|
|
||||||||||||
единичной |
|
|
|
|
|
может |
|
|
быть |
записан в виде |
|||||||||||||||
y = f (t)h(t) . Легко показать, что h(t) |
|
является оригиналом. |
|||||||||||||||||||||||
Найдем |
|
|
его |
|
|
изображение. Для |
|
|
|
|
этого |
|
|
|
|
применим |
|||||||||
преобразование Лапласа |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
¥ |
|
|
- pt |
|
¥ |
|
|
- pt |
|
|
|
b |
|
- pt |
|
|
e- pt |
|
b |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
h(t) Û |
ò |
h(t)e |
|
dt = |
ò |
1× e |
|
|
|
dt = lim |
ò |
e |
|
|
dt |
= lim |
|
|
|
|
= |
||||
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
b®+¥ |
|
|
|
|
b®+¥ - p |
|
|
|
|||||
|
0 |
|
|
|
|
0 |
|
|
|
1 |
|
|
1 |
|
0 |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
= lim ( |
- |
e- pb ). |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
b®+¥ |
|
|
p |
|
p |
|
|
|
|
|
|
|
|
|
|
|
|||
4
|
|
|
|
|
|
e- pb |
|
|
как p = s + is , Re p = s > s0 ³ 0 , |
|
|||||||||
Найдем |
lim |
|
|
. |
Так |
|
а |
||||||||||||
|
|
|
|||||||||||||||||
|
|
|
|
|
b®+¥ |
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
e-ibs |
|
= 1 , то |
|
lim |
e- pb |
= lim |
e-sb |
×e-ibs |
= 0. |
Таким образом, |
||||||||
|
|
|
|||||||||||||||||
|
|
|
p |
|
p |
|
|||||||||||||
|
|
|
|
1 |
|
|
b®+¥ |
|
b®+¥ |
|
|
|
|
||||||
h(t) Û |
. |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
3. Некоторые теоремы об изображении |
|
||||||||||||||
|
|
|
|
|
|
||||||||||||||
|
Теорема 1 ( о существовании изображения). |
|
|||||||||||||||||
|
Всякий |
|
оригинал |
f (t) имеет |
своим изображением |
||||||||||||||
функцию |
комплексного |
|
переменного F ( p) , |
определенную |
в |
||||||||||||||
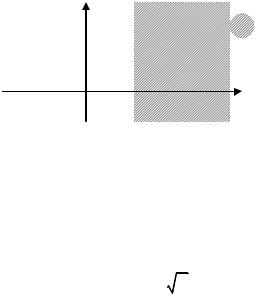
полуплоскости |
Re p = s > s0 , где |
|
s0 |
− |
показатель роста |
||||||||||||||
оригинала (рис. 2). |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
h(t) |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
s ' = Re p > s0 |
|
|
|||
|
|
|
|
|
|
|
|
|
0 |
s0 |
|
|
|
|
|
s |
|
||
|
|
|
|
|
|
|
|
|
|
|
Рис. 2 |
|
|
|
|
|
|||
|
Теорема 2 (о поведении изображения на бесконечности). |
|
|||||||||||||||||
|
Если функция F ( p) - изображение, то |
lim F ( p) = 0. |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Re p®+¥ |
|
|
|
Для этой теоремы нет обратной |
, |
то есть из условия |
||||||||||||||||
|
lim F( p ) = 0 |
не следует, что F ( p) |
− изображение. |
|
|||||||||||||||
Re p®¥ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Пример 1. |
Функции |
F ( p) = |
p , F ( p) = e p , F ( p) = p |
не |
||||||||||||||
стремятся к нулю при Re p ® +¥ и поэтому не могут служить изображениями.
5
Пример 2. |
Функция |
|
|
F ( p) = e- p ® 0 при Re p = s ® +¥ , |
|||||||||||||||||||||||||||||||
но не существует функции f (t) , для |
которой e- p |
|
было |
бы |
|||||||||||||||||||||||||||||||
изображением. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Теорема 3 (о линейности изображения). |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
Если |
|
|
f1 (t) Û F1 ( p) |
|
|
и |
|
|
|
f2 (t) Û F2 ( p) , |
то |
||||||||||||||||||||||||
c1 f1 (t) + c2 f2 (t) Û c1 F1 ( p) + c2 F2 ( p) , |
где |
|
c1 , c2 |
− комплексные |
|||||||||||||||||||||||||||||||
постоянные. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Теорема 4 (об аналитичности изображения). |
|
|
|
||||||||||||||||||||||||||||||||
Если функция F ( p) |
|
|
является |
изображением |
|
некоторого |
|||||||||||||||||||||||||||||
оригинала |
f (t) , то |
|
|
F ( p) |
|
− |
функция |
аналитическая в |
|||||||||||||||||||||||||||
полуплоскости |
Re p = s > s0 , |
|
|
где |
s0 |
|
− |
|
|
показатель |
роста |
||||||||||||||||||||||||
оригинала. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
4. Изображение простейших оригиналов |
|
||||||||||||||||||||||||||||||
1. |
Пусть |
f (t) = c , |
|
где c = const. |
Тогда |
f (t) Û |
c |
, то есть |
|||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|||
c Û |
c |
. Действительно, |
так как 1 Û |
1 |
|
при Re p = s > 0 , то |
|||||||||||||||||||||||||||||
|
|
p |
|||||||||||||||||||||||||||||||||
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
на основании теоремы 3 имеем c ×1 Û c × |
1 |
|
при Re p = s > 0 . |
||||||||||||||||||||||||||||||||
p |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
2. |
|
f (t) = eat . Найдем F ( p) |
по определению |
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
¥ |
|
|
|
|
|
¥ |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
b |
|
|
|
|||
eat Û |
ò |
|
eat ×e- pt dt = |
ò |
e(a - p )t dt = lim |
|
|
|
e(a - p )t |
|
|
= |
|
||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b®+¥ a - p |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
||||||||||||||||
|
|
|
|
0 |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
= |
1 |
|
|
lim (e(a - p )b |
-1) = |
|
1 |
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
a - p b®+¥ |
|
|
|
|
|
|
|
-a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
если Re(a - p) < 0 , и |
|
|
|
1 |
|
|
lim (e(a - p) -1) = ¥ , если |
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
Re(a - p) > 0. |
|
a - p b®+¥ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
at |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Таким образом e |
Û |
|
|
, |
если Re p > Rea. |
|
|
|
|||||||||||||||||||||||||||
p -a |
|
|
|
|
|||||||||||||||||||||||||||||||
6

3. f (t) = coswt , (w − положительное число). Выразим
косинус через показательные функции: cos wt = eiwt + e-iwt . 2
Зная, что eat |
Û |
|
|
|
1 |
|
, при Re p > Rea , и учитывая свойство |
|||||||||||||||||||||||||||||||
p -a |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
линейности изображения, получим |
|
|
|
p |
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
coswt Û |
1 |
( |
1 |
|
|
|
+ |
|
1 |
) = |
. |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 p - iw p + iw p2 + w2 |
|
|
||||||||||||||||||||
Так |
|
как |
|
в |
|
|
|
данном |
случаеa = miw , |
то |
Rea = 0 |
,и |
||||||||||||||||||||||||||
следовательно, coswt Û |
|
|
p |
|
|
|
|
при Re p > 0 . |
|
|
|
|||||||||||||||||||||||||||
|
p2 + w2 |
|
|
|
||||||||||||||||||||||||||||||||||
4. |
f (t) = sin wt , |
(w − положительное число). Проводя |
||||||||||||||||||||||||||||||||||||
рассуждения, |
|
аналогичные |
предыдущим, |
и |
учитывая, |
что |
||||||||||||||||||||||||||||||||
sin wt = |
eiwt - e-iwt |
, получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
2i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
w |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
sin wt Û |
|
|
|
|
|
|
|
|
при Re p > 0 . |
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
p2 + w2 |
|
|
|
|
|||||||||||||||||||||||||||||
5. |
f (t) = ch at , |
( a − положительное число). Запишем ch at |
||||||||||||||||||||||||||||||||||||
в виде ch at = |
eat + e-at |
|
|
. Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
ch at Û |
( |
|
|
+ |
|
) = |
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
p2 - a2 |
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 p - a p + a |
|
|
|
||||||||||||||||||||||
при Re p > Rea = a . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
ch at Û |
|
|
|
|
|
|
|
p |
|
при Re p > a . |
|
|
|
||||||||||||||||||||
|
|
|
|
|
p2 |
- a2 |
|
|
|
|
||||||||||||||||||||||||||||
6. |
f (t) = sh at |
( a − |
положительное |
число). Используя |
||||||||||||||||||||||||||||||||||
|
|
|
sh at = |
|
eat - e-at |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
формулу |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, получим |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
sh at Û |
|
|
|
|
|
|
|
|
|
при Re p > a . |
|
|
|
||||||||||||||||||||
|
|
|
|
|
p2 |
- a2 |
|
|
|
|
||||||||||||||||||||||||||||
7
Пример. Найти изображение заданных функций:
1. 2sin 3t - cos |
|
t |
|
; |
|
2. cos2 t; |
|
|
|
3. sh3 t ; |
|
|
|
|
4. sin2 (t - a) . |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Решение. |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
4 p |
|
|
|
|
|||||||||||||||||||||||||||
1. |
|
2sin 3t - cos |
Û 2 × |
|
|
|
|
|
|
|
|
|
|
- |
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
- |
|
|
|
|
= |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
p2 + 9 |
|
|
|
|
p2 + |
|
|
|
|
|
|
p2 + 9 4 p2 +1 |
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
= |
|
24 p2 + 6 - 4 p3 - 36 p |
= - |
|
|
|
|
|
|
4 p3 +12 p - 6 |
; |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
( p2 + 9)(4 p2 +1) |
|
|
|
|
( p2 + 9)(4 p2 +1) |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
2. cos |
2 |
t = |
1 + cos2t |
= |
|
1 |
|
+ |
1 |
cos 2t = |
1 |
× |
1 |
|
|
+ |
1 |
|
× |
|
|
p |
|
|
= |
|
|
p2+ 2 |
|
; |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 p 2 p |
2 |
+ 4 p( p2 + 4) |
||||||||||||||||||||||||||||||||||||||||||||
|
3 |
t |
= |
|
|
et |
- e-t |
3 |
|
|
= |
|
1 |
|
(e |
3t |
|
- |
3e |
t |
+ |
3e |
-t |
- e |
-3t |
) = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
3. sh |
|
( |
|
|
|
|
|
|
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
= |
1 |
( |
|
1 |
|
- |
3 |
|
+ |
|
3 |
- |
|
1 |
|
|
) = |
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
; |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( p2 -1)( p2 |
- 9) |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
8 |
|
|
|
p - 3 |
|
|
|
|
|
p -1 |
|
|
|
|
p +1 |
|
|
|
|
|
p + 3 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
4. sin2 (t - a) = |
1 - cos 2(t - a) |
= |
1 |
|
- |
1 |
cos 2(t - a) = |
1 |
- |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
1 |
|
|
1 |
|
|
|
|
1 |
|
|
2 |
|
|
|
|
|
|
p |
|
|
|||||||||||||||
- |
(cos 2t ×cos 2a + sin 2t ×sin 2a) Û |
× |
- |
(cos 2a × |
|
+ |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
p2 |
+ 4 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
p |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
+sin 2a × |
|
2 |
|
|
) = |
1 |
( |
1 |
- |
|
|
|
1 |
|
|
|
|
|
|
|
( p cos 2a - 2sin 2a)). |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
p2 + 4 |
|
|
p2 |
|
+ 4 |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
5. Основные теоремы преобразования Лапласа |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Теорема подобия: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
Если |
|
f (t) Û F ( p) , то |
|
|
f (at) Û |
F ( |
) |
|
|
|
для любого a > 0. |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Пример. Найти изображение следующих функций:
а) f (t) = cos mt ×cos nt ; б) f (t) = sin mt ×cos nt.
8
|
Решение. |
)а Преобразовав |
|
|
|
|
|
|
|
f (t) |
|
|
по |
|
|
|
|
формулам |
|||||||||||||||||||||||||||||||||
тригонометрии, |
получим |
|
f (t) = |
1 |
(cos(m - n)t + cos(m + n)t) , |
||||||||||||||||||||||||||||||||||||||||||||||
2 |
|||||||||||||||||||||||||||||||||||||||||||||||||||
и, следовательно, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
F ( p) = |
1 |
( |
|
|
|
|
p |
+ |
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
) = |
|
|
|
|
p( p2 + m2 + n2 ) |
|
|
; |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
p2 + (m+ n)2 |
|
|
( p2 + m2 + n2 )2 |
- 4m2 n2 |
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
2 p2 + (m - n)2 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
б) Аналогично, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m + n |
|
|
|
m - n |
|
|
|
||||||||||||||||||||||
f (t) = |
1 |
|
(sin(m+n)t + sin(m-n)t) Û |
1 |
( |
|
|
+ |
|
|
|
) = |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
p2 + (m-n)2 |
|||||||||||||||||||||||||||||||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 p2 + (m+n)2 |
|
|
|
||||||||||||||||||||||||
= |
|
m( p2 + m2 - n2 ) |
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
( p2 + m2 + n2 )2 - 4m2 n2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
Теорема смещения: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Если |
f (t) Û F ( p) , то eat |
f (t) Û F ( p -a ) |
для любого a Î C |
||||||||||||||||||||||||||||||||||||||||||||||||
при Re p > s0 + Rea. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
Пример1. Найти изображение функций: |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
а) eat |
sin wt; |
б) eat coswt; в) eat |
sh at; г) |
eat ch at. |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
Решение. Так как |
sin wt Û |
|
|
|
|
|
w |
|
|
, coswt Û |
|
|
p |
, |
|
|
|||||||||||||||||||||||||||||||||
|
|
p2 |
|
|
+ w2 |
|
|
p2 |
|
+ w2 |
|
|
|||||||||||||||||||||||||||||||||||||||
sh at Û |
|
|
a |
, ch at Û |
|
|
|
|
p |
|
, |
|
|
|
|
|
|
|
,то применяя |
|
|
теорему |
|||||||||||||||||||||||||||||
p2 - a2 |
|
p2 |
- a2 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
смещения, получим: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p - a |
|
|
|
|
|
|
||||||||||||||||
|
at |
|
|
|
|
|
|
|
|
|
|
w |
|
|
|
|
|
|
|
|
|
|
at |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
а) e |
sin wt Û |
|
|
|
|
; б) |
e |
|
|
coswt Û |
|
|
|
; |
|
|
|
||||||||||||||||||||||||||||||||||
( p - a)2 |
+ w2 |
|
|
|
( p - a)2 + w2 |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
at |
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
at |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p -a |
|
|
|
|
|
|
|
|||||||
в) e |
sh at Û |
|
|
; г) e |
ch at Û |
|
|
. |
|
|
|
||||||||||||||||||||||||||||||||||||||||
( p - a)2 - a2 |
( p - a)2 - a2 |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
Пример 2. Найти изображение функции |
|
f (t) = e-t |
|
sin2 t. |
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
Решение. Представим |
f (t) в виде |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
f (t) = e-t sin2 t = e-t × |
1 - cos 2t |
= |
1 |
e-t |
|
|
- |
1 |
e-t cos 2t. |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
9
Тогда
f (t) Û |
1 |
× |
1 |
- |
1 |
× |
p +1 |
= |
1 |
( |
|
1 |
- |
|
p +1 |
) = |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
2 p +1 2 ( p +1)2 + 4 2 p +1 p2 + 2 p + 5 |
|
||||||||||||||||||
|
= |
|
|
|
|
2 |
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
( p +1)( p2 + 2 p + 5) |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Теорема запаздывания: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Если |
f (t) Û F ( p) , |
то |
|
|
f (t - b) Û e-bp F ( p) |
|
для |
любого |
||||||||||||||
b Î[0, ¥) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
По определению оригинала имеем: |
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
ì f (t - b) |
при t ³ b, |
|
|
|
|
||||||||
|
|
|
|
|
|
|
y = í |
0 |
при t < b. |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
î |
|
|
|
|
|||||||||
|
График |
|
функцииy = f (t - b) |
сдвинут |
по |
оси t |
||||||||||||||||
относительно |
графика |
|
|
функции y = f (t) |
на |
величинуb . |
||||||||||||||||
Процесс, описываемый функцией f (t - b) , |
начинается как бы |
|||||||||||||||||||||
с |
опозданием |
на |
|
|
времяb , |
относительно |
процесса, |
|||||||||||||||
описываемого |
функцией |
f (t) . Отсюда |
и |
появился термин |
||||||||||||||||||
«запаздывание». Исходя из физического толкования, теорему запаздывания можно сформулировать : такзапаздывание оригинала на положительную величинуb соответствует умножению изображения на e-bp .
Пример1. Найти изображение функции f (t) =h(t - 5). Решение. Запишем функцию в виде
ì1 при t ³ 5, f (t) = í
î0 при t < 5.
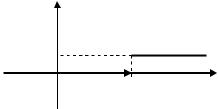
График этой функции(рис. 3): f (t)
0 |
5 |
t |
Рис. 3
10
