Учебное пособие 411

Министерство образования и науки Российской федерации

Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования

«Воронежский государственный архитектурно-строительный университет»

Кафедра высшей математики

МАТЕМАТИЧЕСКАЯ СТАТИСТИКА

методические указания для выполнения контрольной работы №2 для студентов 2-го курса заочного факультета,

обучающихся по направлению подготовки бакалавров «Экономика»

Воронеж 2013

УДК 517.8 ББК 22.17

Составители:

В.Н. Колпачев, М.Д. Гончаров, А.М. Дементьева, В.В. Горяйнов

Математическая статистика: методические указания для выполнения контрольной работы №2 для студ. 2-го курса ЗФ, обуч. по направ. подготовки бакалавров «Экономика» / Воронежский ГАСУ; сост.: В.Н. Колпачев, М.Д. Гончаров, А.М. Дементьева, В.В. Горяйнов. – Воронеж, 2013. –26 с.

Методические указания содержат краткие сведения по математической статистике и рекомендации по решению задач, входящих в контрольную работу, программу и задания для контрольной работы по разделу «Математическая статистика» курса «Теория вероятностей и математическая статистика». Даны ссылки на литературу, которой можно пользоваться при подготовке к экзамену и выполнении контрольной работы.

Предназначены для студентов 2-го курса заочного факультета Воронежского ГАСУ, обучающихся по направлению подготовки бакалавров «Экономика».

Библиогр.:6 назв.

УДК 517.8 ББК 22.17

Печатается по решению научно–методического совета Воронежского ГАСУ

Рецензент – Е.И. Макаров, доктор экономических наук, профессор кафедры экономики и основ предпринимательства Воронежского ГАСУ

2

ПРЕДМЕТ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ

Математическая статистика – раздел математики, занимающийся обработкой статистических данных с целью установления закономерностей, присущих массовым случайным явлениям. Статистические данные представляют собой сведения о том, какие значения принял в результате наблюдений интересующий нас признак (случайная величина). Методы математической статистики разработаны на основе методов теории вероятностей.

Математическая статистика возникла в XVI в. и развивалась параллельно с теорией вероятностей. В XIX–XX вв. большой вклад в развитие математической статистики внесли П.Л. Чебышев, А.А. Марков, А.Н. Ляпунов, К. Гаусс, К. Пирсон, А.Н. Колмогоров, Р. Фишер, Ю. Нейман и другие известные уче- ные-математики.

ОБЩИЕ РЕКОМЕНДАЦИИ К ВЫПОЛНЕНИЮ КОНТРОЛЬНОЙ РАБОТЫ

Данная контрольная работа является второй из двух работ, выполняемых студентами по курсу «Теория вероятностей и математическая статистика». Контрольная работа должна быть выполнена и зачтена для получения допуска к экзамену. Контрольная работа выполняется в отдельной тетради. Условия задач следует переписывать полностью. Оформление должно быть аккуратным, записи четкими, а решение должно сопровождаться подробными пояснениями с необходимыми ссылками на теорию.

Приступать к выполнению контрольной работы можно лишь после изучения необходимого теоретического материала и разбора решения аналогичных задач, используя рекомендации, приведенные в методических указаниях.

В контрольной работе студент выполняет вариант, номер которого совпадает с последней цифрой шифра его зачетной книжки. Если этой цифрой является ноль, то следует выполнять десятый вариант.

ВОПРОСЫ ПРОГРАММЫ К КОНТРОЛЬНОЙ РАБОТЕ №2

1.Понятие выборки значений случайной величины, полученных опытным путем. Вариационный ряд.

2.Построение полигона частот (относительных частот) по выборке значений дискретной случайной величины.

3.Интервальное распределение и гистограмма, составленные по выборке значений непрерывной случайной величины.

4.Вариационный ряд, сопоставляемый интервальному распределению. Эмпирическая функция распределения.

3

5.Точечные оценки числовых параметров M (X ), D (X ), σ (X ) случай-

ной величины на основе выборки: выборочное среднее xв , выборочная дисперсия Dв , выборочное среднее квадратическое отклонение σв .

6.Несмещенность и состоятельность точечных оценок. Исправленная выборочная дисперсия и оценка S для σ (X ).

7.Понятие интервальной оценки числового параметра случайной величины. Точность и надежность (доверительная вероятность) интервальной оценки.

8.Интервальные оценки для M (X ) и D (X ) нормально распределенной

случайной величины на основе выборки.

9.Понятие о корреляционном и регрессионном анализе.

10.Коэффициент корреляции.

11.Выборочное уравнение прямой регрессии.

Литература: [1, гл. XX, §§27-29], [2, гл 15 §§ 1-5, 7-10, 13-19], [3, гл. 9, гл. 10, §§1,4], [4, гл. V, §§17,18], [5, лекции 8 – 10], [6]

СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ

1.Пискунов, Н.С. Дифференциальное и интегральное исчисления: в 2 т. /

Н.С. Пискунов. – М.: ИНТЕГРАЛ–ПРЕСС, 2002. – Т. 2. – 544 с.

2.Гмурман В.Е. Теория вероятностей и математическая статистика / В.Е.

Гмурман. – М.: Высшая школа, 2003. – 479 с.

3.Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике / В.Е. Гмурман. – М.: Высшая школа, 2003. – 405 с

4.Данко, П.Е. Высшая математика в упражнениях и задачах: в 2 ч. / П.Е.

Данко, А. Г. Попов, Т. Я. Кожевникова.– М.: Издательский дом «ОНИКС 21

Век»: Мир и Образование, 2003. – Ч.2.– 416 с.

5.Алейников С.М. Элементы теории вероятностей и математической статистики: курс лекций / С.М. Алейников, А.М. Дементьева; Воронеж. гос. арх.– строит. ун–т. – Воронеж, 2002. – 84 с.

6.Теория вероятностей: Методические указания и контрольные задания к типовому расчету № 8 по курсу математики для студ. 2-го курса / Воронежский гос. арх.-строит. ун.-т; Составители: Л.В. Акчурина, А.Б. Кущев, Е.И. Ханкин –

Воронеж, 2010. – 46 с.

Указания по обращению к рекомендуемой литературе даны в тексте программы. Номер источников из приведенного выше списка пишут в квадратных скобках. Например, [2, гл. 1-4, 5 §§ 1,2,3] обозначает учебник Гмурман В.Е. «Теория вероятностей и математическая статистика» главы 1-4 и глава 5, §§ 1,2,3.

4

Таблица 1 Статистическое распределение частот выборки

Здесь исходный интервал, в котором заключены все n наблюдаемых значений признака, разбит точками xi (i =1,..., n) на некоторое количество k рав-

ных интервалов длины h = xi+1 − xi , а ni - количество вариант, попавших в i – й

интервал. Тогда легко строится гистограмма частот – ступенчатая фигура, состоящая из прямоугольников , основания которых есть частичные интервалы длины h , а высоты равны отношению ni h . Если вместо ni взять относитель-

ные частоты wi , то полученная гистограмма относительных частот будет

статистическим аналогом функции плотности вероятности изучаемого признака.

В качестве статистического аналога функции распределения случайной величины вводится эмпирическая функция распределения

F * (x)= nnx

где nx – число вариант, меньших x; n – объем выборки.

Рассмотрим следующую практическую задачу. Агроном хочет прикинуть, каков будет урожай зерновых на всех полях (естественно, что на разных полях урожайность может существенно отличаться). На каждом поле скашивается небольшой кусок и оценивается урожайность, затем берут интервал (xmin , xmax ), где

xmin - минимальная урожайность, а xmax - максимальная урожайность, и делят его

на k частей. Затем считают количество полей с урожайностью, попадающей в каждый интервал, и составляют соответствующую таблицу.

Пример 1. Пусть статистическое распределение урожайности зерновых на выборочных участках полей совхоза задается таблицей

6

Требуется: 1). Построить гистограмму относительных частот; 2). Перейти к вариантам и построить полигон частот; 3). Построить эмпирическую функцию распределения.

Решение. Объем выборки n равен 20+60+120+190+70+40=500. По фор-

муле (1) найдем относительные частоты и выпишем исходную таблицу с относительными частотами:

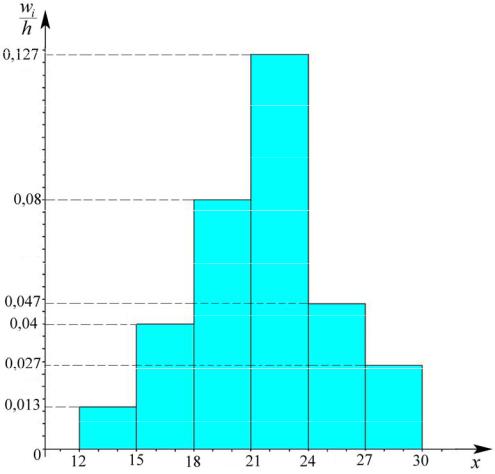
Для построения гистограммы относительных частот на оси абсцисс отложим частичные интервалы длины h =3, а над ними проведем горизонтальные отрезки высоты wi 3. Для лучшей наглядности выберем на осях координат

разный масштаб (рис. 1).

Рис. 1. Гистограмма относительных частот

7

Перейдем к вариантам, положив их равными серединам частичных интервалов xi = (ai + ai +1 )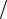2 , где a1 , a2 , …, ak +1 – концы интервалов. Соответст-

венно исходная таблица превратится в следующую:

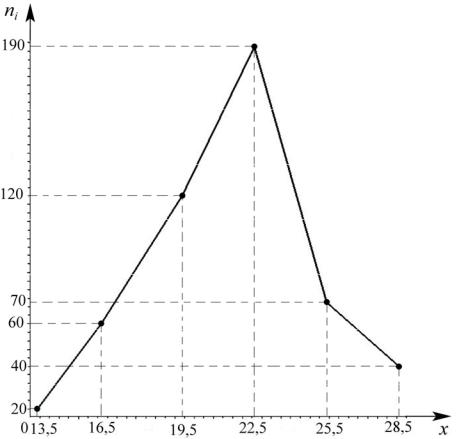
Построим на плоскости точки (xi , ni ) (i =1, 2,...6) и, соединив соседние точки, получим полигон частот (рис.2).

Рис. 2. Полигон частот

Аналогично тому, как находилась функция распределения F(x) в теории вероятностей можно выписать эмпирическую функцию распределения F* (x), в

которой происходит накапливание относительной частоты (вместо вероятности) при движении по оси Ox от « −∞» до « +∞»:

8

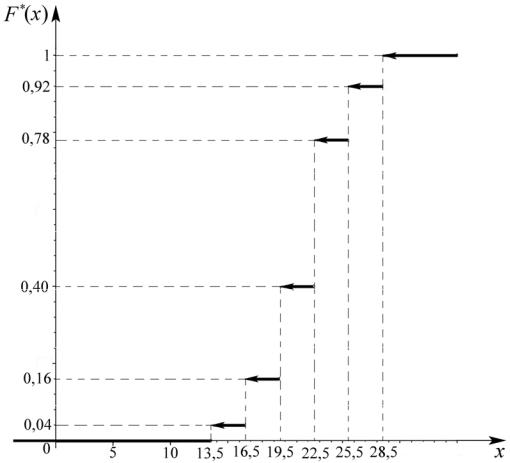
Постоим график эмпирической функции распределения (рис. 3)

Рис. 3. Эмпирическая функция распределения

Выборочные числовые характеристики

Аналогично таким числовым характеристикам случайной величины, как математическое ожидание, дисперсия и среднее квадратическое отклонение для выборки определяются соответственно выборочные числовые характеристики:

выборочное среднее, выборочная дисперсия, выборочное среднее квадра-

9

тическое отклонение:

Пример 2. В условиях предыдущего примера найти xв , Dв , σв . Решение. По таблице

x2 = (13,5)2 20 +(16,5)2 60 +(19,5)2 120 +(22,5)2 190 +(25,5)2 70 +(28,5)2 40 = 500

=479,61.

10